この文書の位置付け
Status of this Document
この節では, 公表された時点でのこの文書の位置付けについて述べます. 他の文書がこの文書に取って代わってもよいです. 現時点でのW3Cの公表した文書の一覧とこの技術報告書の最新版は, W3C技術報告書の索引(http://www.w3.org/TR/)で見ることができます.
This section describes the status of this document at the time of its publication. Other documents may supersede this document. A list of current W3C publications and the latest revision of this technical report can be found in the W3C technical reports index at http://www.w3.org/TR/.
このメモは, MathMLにおけるアラビア語の数学表記の独立した議論です, このメモは, MathML 2勧告(第2版)[MathML22e]を用いたアラビア語の数学表現を取り扱うための手引きを提供し, 将来版への拡張を提案します.
This Note is a self-contained discussion of Arabic mathematical notation in
MathML. It provides guidelines for the handling of Arabic mathematical
presentation using MathML 2
Recommendation (2nd Edition) [MathML22e]
and suggests extensions for a future revision.
このメモは, W3C数学事業の一部である数学関連部会(W3C会員限定)の参加者によって書かれてきました. この文書(英語版)に対する意見を述べたり, 間違いを報告したりするには, 公式な記録を伴うメーリングリストwww-math@w3.orgにメールして下さい.(訳注:この文書(日本語版)に対する意見を述べたり, 間違いを報告したりするには, soco__kankyo@hotmail.comにメールして下さい.)
This Note has been written by participants in the Math Interest Group (W3C
members only) which is part of the W3C Math activity. Please direct
comments and report errors in this document to www-math@w3.org, a mailing list with a public archive.
関連部会のメモとしての公表は, W3C会員の賛同を得たものではありません. この文書は草稿であり, いつでも他の文書により, 更新されたり, 置き換えられたり, 破棄されたりしてもよいです. 作業の経過によらず, この文書を掲載することが不適当になります.
Publication as a Interest Group Note does not imply endorsement by the W3C Membership. This is a draft document and may be updated, replaced or obsoleted by other documents at any time. It is inappropriate to cite this document as other than work in progress.
1 導入
Introduction
ワールド・ワイド・ウェブがより世界に広まっていくにつれて, 世界のたくさんの言語, 書体, 文化を包含することが急務となってきています. 数学用マークアップ言語(MathML)[MathML22e]を開発したものの, そのことは, ヨーロッパ以外の言語や書体を故意または明白に除外しており, 焦点は, ヨーロッパの言語で用いられる表記の枠組みに当たっていました. 確かに, それらの表記のほとんどは, 他の言語の文脈でも変更せずに利用されていました. しかしながら, 言語の中には, 歴史的な理由から, また, 様々な筆記体系に適合するように, 導入された様々な種類のものがあり, MathMLは, 改善された国際的な対応のために, それらに(特にそれらの様々な種類のものや歴史的な文書を必要とする教育題材に)適合すべきです.
As the World Wide Web becomes more world wide, inclusion of the world's many languages,
scripts and cultures becomes critical. Although the development of the Mathematical
Markup Language (MathML) [MathML22e], was neither intentionally nor
explicitly exclusive of non-European languages and scripts,
the focus was on the notational schema used with European languages. Indeed, most of these
notations are used unchanged in many other contexts. However, there are variations introduced
in some languages, either for historical reasons, or to fit within various writing systems,
which MathML should accommodate for improved international support (in particular educational
material requiring these variations, or historical documents).
ヨーロッパの言語は, 左から右へ(LTRで)書かれる一方, 他の言語の中で特にアラビア語は, 右から左へ(RTLで)書かれます. アラビア語の数学の文章において, たくさんの同じ表記構造が使われていますが, それらは文化的な背景に依存して反転されたり, 鏡文字になったりしてよいことが分かるでしょう. それらを数学の方向と呼びます. 数学の方向は, 文章の方向と同じように必要なわけではありません. さらに, 数学の題材は, アラビア語とヨーロッパの言語両方に由来する文字や記号を一般に含んでもよく, どのようにユニコードの双方向のアルゴリズム[ユニコードBiDi]が適用されるべきかという問いが現れます. 最終的に, 様々な追加の記号や書き方が特別な方法で使用されてもよいです.
While European languages are written left to right (LTR), Arabic, among others, is
written right to left (RTL). We will see that in Arabic mathematical texts many of the
same notational constructs are used, but may be reversed or mirrored,
depending on the cultural context; what we will call a mathematical directionality.
The mathematical directionality is not necessarily the same as the text directionality.
Moreover, since the mathematical material may commonly contain text and symbols coming from
both Arabic and European languages, the question of how the Unicode bidirectional algorithm
[UnicodeBiDi] should be applied arises.
Finally, several additional symbols and writing styles may be used in special ways.
![[Arabic Script samples]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/khtout.png)
アラビア語の筆記体は, ヨーロッパの言語がフォントの多様性で豊かになったように, 書き方の多様性で豊かになります. 上の画像は, アラビア語の筆記体書体の多様性を説明しています. 各言葉は, 関係する書体の名前です. ヨーロッパの数学が, 太字やフラクタルや他の書体を用いることで利用可能な別個の記号の集合を拡張したのと同じ方法で, ただし, 典型的に線を変えたり, テールや他の拡張を加えたりすることで, アラビア語の数学を拡張します.
Arabic Calligraphy is enriched by a variety of writing styles,
as European writing benefits from a variety of fonts. The graphic above illustrates
a variety of Arabic calligraphic styles; each word is the name of the corresponding style.
In the same way that European mathematics broadens the set of distinct symbols available by
using bold face, Fraktur or other styles, so does Arabic mathematics but typically
by varying strokes, adding tails or other extensions.
コンテントMathML([MathML22e], 第4章)で記述された数学の部分は, 一般に言語に中立です. たとえ, 変数名の選択が文化的な背景を暗に意味してよいとしてもです. コンテントMathMLは, 数学の普遍的な意味を表すことを意図しています. 一方で, プレゼンテーションMathML([MathML22e], 第3章)で記述された数学の部分は, 式の視覚的な印象を伝えています. その印象は, 特定の言語や表記の慣習, 実際のところ, 関係する科学分野さえどうしても対象とします. このメモにおいて, この関心事の分離を展開し, 形式化します. プレゼンテーションMathMLは, 使用されている視覚的な表記の明瞭な文字の表現であるべきです.
A given piece of mathematics marked up in
Content MathML
([MathML22e], chapter 4), is generally language-neutral — although the
choices for variable names may imply a cultural context —
it intends to represent the universal meaning of the mathematics.
A given piece of mathematics marked up in
Presentation MathML
([MathML22e], chapter 3),
on the other hand, conveys the visual appearance of the expression. That appearance
necessarily targets a specific language and notational conventions, indeed even of
the scientific discipline involved.
In this Note, we amplify and formalize this segregation of concerns:
Presentation MathML should be a fairly literal
representation of the visual notation to be used.
どの記号を総和に用いるのか. どの名前を正接に用いるのかといった全ての地域対応の課題を描画ソフトウェアではなくプレゼンテーションMathMLの生成ソフトウェアに任せています. このことは, 例えば, ピリオドをコンマに置換するかどうかを決めると同時に, 何の数字が意図されているか推測することを, ひょっとしたら間違って推測することを避けられます. よって, 地域対応は, MathML素子要素の中に, 何の文字列データが配置されているのか選択することを引き起こします. ただし, その選択は, プレゼンテーションMathMLの一部の中に留まります.
We relegate all localization issues
— which symbol to use for summation, which name to use for tangent, what
format to use for numbers — to the generator of the Presentation MathML,
rather than the renderer. This avoids guessing, perhaps wrongly, what number is
intended while deciding whether to replace periods by commas, for example. Thus,
localization entails the choice of what
text content to place within MathML's token elements, but that choice is already fixed
within a given piece of Presentation MathML.
このメモにおいて, アラビア語やアラビア書体を用いて書く言語の現在の利用における全ての表記の慣習を, 他のものに対して1つの形式を優先することなしに, 調査しようと試みています. 必要とされる拡張を提案することでMathML仕様書を明瞭にすることを目的としており, そのためMathMLは, 可能な限り広い範囲を網羅します. それでも, 他の言語, 特に上から下に書かれる言語に影響を与える課題の徹底した分析は, 将来の研究テーマです. アラビア語における主眼点は, ここで述べる課題を強く表している, アラビア語の文脈の中でMathMLへの増加している興味や利用を部分的に反映することです. 将来の研究に対する他のテーマは, どのようにコンテントMathMLが適切に地域対応したプレゼンテーションMathMLへの変換に最善の対応をするかということです.
In this Note, we have attempted to examine all notational conventions in current
use with Arabic and languages written using Arabic script, without giving preference
to one form over another.
We aim to clarify the specification of MathML, proposing extensions where needed,
so that MathML has the broadest coverage possible. Nevertheless, an in-depth analysis of issues
affecting other languages, particularly those written top to bottom is a topic for future study.
The emphasis on Arabic languages is partly a reflection of an increased interest in, and
usage of, MathML in Arabic language contexts that have highlighted the issues described here.
Another topic for future study is how Content MathML might best support the transformation
to appropriately localized Presentation MathML.
2 アラビア書体の機能
Some Features of Arabic Script
数学表記を掘り下げる前に, それらの表記は, アラビア書体の機能や, どのようにユニコードがそれらの機能を処理してるかを説明するのに役立つでしょう.
Before delving into mathematical notations, it will help to describe some
of the features of Arabic script, and how Unicode deals with these features.
2.1 文章の方向
Text Direction
ヨーロッパの言語は左から右へ(LTRで)書かれる一方, アラビア語は右から左へ(RTLで)書かれます. ユニコードは, それらの言語の個々の文字にコードポイントを定義するのみではなく, 各文字の指向性を記録することで, それらの書体に対応しています.
While European languages are written from left to right (LTR), Arabic is written from
right to left (RTL). Unicode supports these scripts by not only defining codepoints
for the individual characters of these languages, but by recording the directionality
of each character.
LTRとRTLの文字の混在が文章の中で生じたとき(すなわち, アラビア語の言葉を含む英語の文章のような, 双方向の文章, もしくはBiDi文章のとき), ユニコードの双方向のアルゴリズム[ユニコードBiDi]が, その文字を表示するかといった順番を説明します. (単独のアラビア語の言葉のような)全ての隣接する強く型付けされたRTL文字列は, 右から左の順番で示され, また, 逆に, 強く型付けされたLTR文字列も同様です. 同じ方向を持った文字列の一団を一方向の一続きと呼びます.
When a mixture of LTR and RTL characters appear in text (ie. bidirectional or BiDi text,
such as an English text that includes Arabic words),
Unicode's bidirectional algorithm [UnicodeBiDi] describes the order in which
the characters will be displayed. All adjacent strongly-typed RTL characters (such as a
in a single Arabic word) will be presented in right-to-left order, and vice versa for
strongly-typed LTR characters. A cluster of characters with the same directionality
is called a directional run.
どの与えられた"段落"の中でも, 一方向の一続きは, 全体の一方向の文脈によって順番が決まります. 双方向のアルゴリズムは, 高い階層の通信規約に, 構造化された文章のどの部分が"段落"の一部を成すか決めることを認めています. 例えば, HTMLにおいてブロックレベル要素は, 段落部分として扱われます. 一番上の階層のhtmlタグは, dir属性を用いて下の階層の要素において変更することも可能な文脈の方向を決めます.
Within any given "paragraph", directional runs are then ordered according to the
overall directional context. The bidirectional algorithm allows for higher-level
protocols to determine which segments of a structured text constitute "paragraphs"
in this sense. For example, in HTML block-level elements are taken as the
paragraph segments. The top-level html tag determines the directional context
which can be changed on lower-level elements using the dir attribute.
双方向の文章に対する寛大な導入については, [ユニコードBiDi導入]を参照して下さい.
For a gentle introduction to bidirectional text, see
[UnicodeBiDiIntro].
2.2 字形の形成
Glyph Shaping
アラビア語は筆記体なので, 言葉の中の文字列は, 典型的に1つにつなげられてます. そのような筆記体の中の文章が一連の文字列によって指定されているとき, 形成と呼ばれる工程が, 文字の字形を調整するかつなげるかするために用いられます. 単独の文字から成るアラビア語の言葉において, その文字は"独立"形で描かれます. 複数の文字の言葉において, 代わりの形が一般に場所に基づいて使用されます. 最初の(一番右の)文字は"語頭"形で描かれ, 最後の(一番左の)文字は"語尾"形と成り, そして, 途中の文字はどれも"語中"形です.
As Arabic is a calligraphic script, letters within words are typically joined together.
When text in such calligraphic scripts is specified by character sequences, a
process called shaping is used to blend, or connect the character glyphs.
In Arabic words consisting of a single character, that character is drawn in the "isolated"
style. In multi-character words, alternative shapes are generally used depending on position:
the first (rightmost) character is drawn in its "initial" shape,
the last (leftmost) character gets its "final" shape, and any characters in the middle
are of the "medial" shape.
独立形の文字غ ي رと字形の形成の結果غيرを比べて下さい.
Compare the isolated characters غ ي ر
to the result of glyph shaping غير.
2.3 鏡文字
Mirroring
文字の中には, 抽象的に考えて, たくさんの言語で同じ意味を持つものがありますが, RTLの言語で用いられる形が, ざっくりLTRの言語で用いられる形の鏡文字となっているものもあります. かっこや引用符はそのような文字です. ユニコードは, そのような状況を, 鏡文字としてコードポイントを示すことで処理しています. このことは, RTLの文脈で現れた場合に, 代わりの字形がその文字に用いられることを意味します.
Some characters, viewed abstractly, have the same meaning in many languages,
but the form used in RTL languages are the roughly the mirror image of the
form used in LTR languages. Parentheses and quotation marks are such characters.
Unicode deals with these cases by marking some codepoints as mirrored, meaning
that an alternate glyph will be used for the character if it appears in a RTL context.
鏡文字の記号は, ユニコード([ユニコードBiDi]の第6節鏡文字参照)によって, 実際のところ正確な鏡文字であることを必要としていません. 確かに, それらの記号は羽毛の先端(カラム)が平らな四角形ではないことが, アラビア語の筆記体の重要な点と考えられています. 書き手はペンを握っているので, 大きい方の端は, ベースラインと概ね70°の角を成します. この操作は, 文字を描く工程の間じゅう保持されます. さらに, アラビア語の書き方は右から左なので, 太線は, 左上から右下へ向かう部分の辺りで提供されることもあります. 逆に, 右上から左下に向かう部分は少し細くなるでしょう. よってアラビア語の総和記号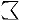 は, 例えば, シグマ
は, 例えば, シグマ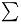 の単純な鏡文字
の単純な鏡文字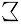 ではありません.
ではありません.
Note that mirrored symbols are not required by Unicode (See
Mirroring
in [UnicodeBiDi], section 6) to be literally
the exact mirror image. Indeed, it is considered an important point of Arabic calligraphy
that they are not: the feather's head (kalam) is a flat rectangle. The writer holds the pen so that
the largest side makes an angle of approximately 70° with the baseline.
This orientation is kept throughout the process of drawing the character.
Furthermore, as Arabic writing goes from right to left, some boldness is produced
around segments running from top left toward the bottom right and conversely,
segments from top right to the bottom left will rather be slim.
Thus, the Arabic sum symbol 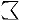 ,
for example, is not simply the mirror image
,
for example, is not simply the mirror image
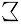 of sigma
of sigma 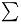 .
.
2.4 数字の体系
Number Systems
様々な数字の体系が, アラビア語の中で用いられます.
There are several decimal numeral systems in use in Arabic:
体系
System | ユニコード
Unicode | 数字
Digits | 描画例
Image | 地域
Regions |
|---|
ヨーロッパ
European | U0030-U0039 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | マグリブ(例えば, モロッコ), ヨーロッパ
Maghreb Arab (eg. Morocco), as well as European |
|---|
アラビア-インド
Arabic-Indic | U0660-U0669 | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | ![[Image of Arabic-Indic Digits]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arind.png) | マシュリク(例えば, エジプト)
Machrek Arab (eg. Egypt) |
|---|
東アラビア-インド
Eastern Arabic-Indic | U06F0-U06F9 | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ![[Image of Eastern Arabic-Indic Digits]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/esarind.png) | イラン
Iran |
|---|
3 数学表記の例示
Comparison of Mathematical Notations
数学の中身の見本を選出したり, それらが異なる言語や文化で典型的にどのように描画されるか比較したりすることで, 表記の様々な領域を探求していきます. 英語とフランス語の両方の文脈で見受けられる構成の式から始めます.
We will explore the spectrum of notations by choosing some samples of mathematical
content and comparing how they would typically be rendered for different languages and cultures.
We begin with an expression formatted as it might be seen in both English
and French contexts.
形式
Style | 描画例
Image | MathML |
|---|
英語
English | ![[Image of formula in English style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/expren.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> if </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> if </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">S</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tan</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> otherwise </mtext>
<mrow>
<mo>(</mo>
<mtext>with </mtext>
<mi>π</mi>
<mo>≃</mo>
<mn>3.141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
フランス語
French | ![[Image of formula in French style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfr.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> si </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> si </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> sinon </mtext>
<mrow>
<mo>(</mo>
<mtext>avec </mtext>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
構造上, これらの式は同一です. 名前, 数字の書式, もちろんつなぎの言葉として用いられる言語での違いは, 全て地域対応によるものです. それらの違いは, MathML素子要素の中の異なる文字列の中身に純粋に影響されています.
Structurally, the expressions are identical. The differences in names,
number formatting and of course the language used for the connecting words are all
due to localization. They are effected purely by
differing textual content within the MathML token elements.
後の節で, アラビア語の文章の中で数学のために用いられる3つの一般的な形式について考察します. モロッコ, マグリブ, マシュリクという用語は, それらの書式が使われている一般的な地理的な範囲を示すのに用いられますが, 地域の間の明確に定義された境界はありません.
In the following sections, we will examine three common styles used
for mathematics within Arabic texts. The terms Moroccan, Maghreb and Machrek will be
used to indicate the general geographic areas where these styles are used, but
there are no clearly defined borders between the regions.
3.1 アラビア語の表記:モロッコ形式
Arabic Notation; Moroccan Style
モロッコで数式を書く現在の方法は, 密接にフランス語の形式に関係しています.
The current way of writing mathematical expressions in Morocco,
is closely related to the French style:
形式
Style | 描画例
Image | MathML |
|---|
モロッコ
Moroccan | ![[Image of formula in Moroccan style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfrm.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>إذاكان </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>إذاكان </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>غيرذلك </mtext>
<mrow>
<mo>(</mo>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mtext>مع</mtext>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
数学がRTLの言語(アラビア語)に埋め込まれているにも関わらず, 数学の方向はLTRのままです.ただし, 数学をつなぐ言葉や言い回しがRTLのアラビア語であっても, (最新のMathML描画ソフトウェアは形成を行わないにも関わらず)字形の形成を条件とすべきです. よって, それらの言い回しは, (for "if"(訳注:"~の場合"の意味)に対しては)"إذاكان", ("otherwise"(訳注:"そうでない場合"の意味)に対しては)"غيرذلك"として, ("with"(訳注:"そうでない場合"の意味)に対しては)"مع"として現れるべきです.
Although the mathematics would be embedded within a RTL language (Arabic),
its directionality is still LTR. The connecting words and phrases within the math, however,
are RTL Arabic, and should be subject to glyph shaping
(although some current MathML renderers are not doing this).
Thus these phrases should appear as
"إذاكان" (for "if"),
"غيرذلك" (for "otherwise")
and "مع" (for "with").
同様に, 双方向のアルゴリズム[ユニコードBiDi]が, HTMLでの「ように高い階層ではなく個々の文章や素子要素に適用されるべきであることが暗示されます. すなわち, 素子要素は段落部分のように挙動します. これらの考察においてさえ, ("otherwise (with pi=3.141)"(訳注:"そうでない場合(pi=3.141を伴って)"の意味)の)最後の節での言い回しの順番は問題があります. "pi=3.141"というmrowを"otherwise (with"と")"といった2つのmtextで明らかに挟んでいるマークアップで, それぞれ間違った順番を生じるでしょう. 正確な描画は, MathML 2.0で認められていないmtextの中にmathを埋め込むことができる必要があるように思われます. ただし, たとえそうでも, 望んだ順番は, 2つの分割されたmtext要素としてマークアップされることを必要とするでしょう. 1つは"otherwise", もう1つは"(with pi=3.141)"です. 数学関連部会は, そのような埋込の可能性を正確に考察しています. 上記の例は, 人工的に"pi=3.141"の後の"with"をアラビア語の言葉で置き換えることで記述しました.
Also, the indication is that the bidirectional algorithm [UnicodeBiDi] should be
applied to individual text and token elements, rather than at a higher level as in HTML;
that is, the token elements act as paragraph segments.
Even with these considerations, the ordering of phrases within the last clause
(for "otherwise (with pi=3.141)") is problematic. The obvious markup sandwiching
an mrow for "pi=3.141" between two mtext's for "otherwise (with" and ")", respectively,
would yield an incorrect ordering. A correct rendering seems to require the possibility
of embedding math within mtext, which is not possible in MathML 2.0.
But even then, the desired ordering would need to be marked up as two separate mtext elements:
one for "otherwise", and one for "(with pi=3.141)". The Math Interest Group is currently
considering the possibilities of such embedding. The example above was marked up by
artificially placing the Arabic word for "with" after the "pi=3.141".
そのような課題を与えられた場合, つなぐ言い回しの使用を最小限にし, 単純な句読法を提供することが 時には有利です. 例えば次のようにです.
Given such issues, it is sometimes advantageous to minimize the use of
connecting phrases, with preference to simple punctuation, such as:
形式
Style | 描画例
Image | MathML |
|---|
モロッコ
Moroccan | ![[Image of simplified formula in Moroccan style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfrn.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mrow>
<mo>(</mo>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
3.2 アラビア語の表記:マグリブ形式
Arabic Notation; Maghreb Style
数学表記のマグリブ形式は, 広く北アフリカで使用されています.
The Maghreb style of notation is widely used in North Africa:
形式
Style | 描画例
Image | MathML |
|---|
マグリブ
Maghreb | ![[Image of formula in Maghreb style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprare.png) | 試作前の段階
Not yet attempted |
|---|
ここで, 最も目立った違いは, 全ての数字の配置が前で示した例の鏡文字になっていることです. つまり, 数学の方向はRTLです. さらに, 記号(例えば, ∑, <, ∈)の中には, 上手く鏡文字になっているものあります. よって, 数学の方向を指定し, 適切な記号がユニコードで利用可能で鏡文字として記述できることを保証する方法が必要です.
Here, the most striking difference is that the overall mathematical
layout is the mirror image of the preceding examples, that is,
the mathematical directionality is RTL. Further, some symbols
(eg ∑, <, ∈) are mirrored as well.
Thus, we need a means of specifying the mathematical directionality,
and assuring that the appropriate symbols are available in Unicode and are marked as mirrored.
残りの違いは, アラビア語の記号のよりはっきりした利用によるものです. (アラビア語の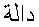 = "function"の頭文字である)ダール
= "function"の頭文字である)ダール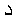 , アラビア文字バー
, アラビア文字バー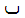 , そして(点無しの)正接に対する関数名を省略した文字
, そして(点無しの)正接に対する関数名を省略した文字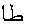 . そのうえ, これらの違いは, 地域対応の範疇に分類されますが, ユニコードの双方向のアルゴリズムは, 字形の形成に従って素子要素に個別に適用すべきという意見を補強しています.
. そのうえ, これらの違いは, 地域対応の範疇に分類されますが, ユニコードの双方向のアルゴリズムは, 字形の形成に従って素子要素に個別に適用すべきという意見を補強しています.
The remaining differences are due to a more pronounced use of Arabic symbols:
DAL 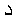 (as the initial
of
(as the initial
of 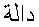 = "function" in Arabic);
the Arabic letter BEH
= "function" in Arabic);
the Arabic letter BEH 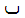 ,
and the letters of the function name abbreviation
,
and the letters of the function name abbreviation 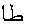 for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.
for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.
3.3 アラビア語の表記:マシュリク形式
Arabic Notation; Machrek Style
最後のアラビア語の例として, 中東で一般的に使用されるマシュリク形式について考察します.
As the final Arabic example, we consider the Machrek style generally used in the Middle East.
形式
Style | 描画例
Image | MathML |
|---|
マシュリク
Machrek | ![[Image of formula in Machrek style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprarw.png) | 試作前の段階
Not yet attempted |
|---|
マシュリク形式とマグリブ形式の間の大部分の違いは, 本質的に地域対応によるものです. 特別なアラビア語の記号 は, (アラビア語の
は, (アラビア語の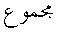 = "sum"の頭文字であり)総和に用いられています. 別の文字
= "sum"の頭文字であり)総和に用いられています. 別の文字 は, (アラビア語の"関数"
は, (アラビア語の"関数" の頭文字であり)関数に用いられています. 初等関数の名前を省略した文字
の頭文字であり)関数に用いられています. 初等関数の名前を省略した文字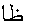 は, 点を持ちます. そして, 数字の形式は, アラビア・インド数字を使用し, 数字の区切りに対してはコンマを使用します(ただし, 文章で使われるアラビア語のコンマと同じではありません).
は, 点を持ちます. そして, 数字の形式は, アラビア・インド数字を使用し, 数字の区切りに対してはコンマを使用します(ただし, 文章で使われるアラビア語のコンマと同じではありません).
Most differences between the Machrek and Maghreb styles are essentially due to localization:
a specifically Arabic symbol  is used for the summation
(initial of
is used for the summation
(initial of 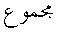 = "sum" in Arabic);
a different letter
= "sum" in Arabic);
a different letter  is used for the function
(initial of
is used for the function
(initial of  , also "function" in Arabic);
the letters of the elementary function name abbreviation
, also "function" in Arabic);
the letters of the elementary function name abbreviation
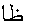 are with dots;
and a number format using Arabic-Indic digits and a comma for the decimal separator (but not
the same as the Arabic comma used in text).
are with dots;
and a number format using Arabic-Indic digits and a comma for the decimal separator (but not
the same as the Arabic comma used in text).
総和に対して用いる記号, ヨーロッパの総和記号がギリシア文字シグマと別個のものであるように, 可能な限りアラビア文字とは別個のコードポイントをもつ数学記号であるべきです. この点は, アラビア語の総積にも適用されます.
Note that the symbol used for summation should probably be a mathematical symbol
with a codepoint distinct from the Arabic letter, as the European summation symbol is
distinct from the Greek Sigma. This point also applies to the Arabic product.
3.4 追加のアラビア語の表記
Additional Arabic Notations
2つ追加の独特の表記が, 結合した記号, すなわち階乗と2項係数に関係しています.
Two additional unique notations involve combinatorics, namely the factorial and
binomial coefficients:
形式
Style | 描画例
Image | MathML |
|---|
英語
English | ![[Image of 12 factorial in english style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/drbcen.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow><mn>12</mn><mo>!</mo></mrow>
</math>
|
|---|
アラビア語
Arabic | ![[Image of 12 factorial in Arabic style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/drbc.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block" dir="rtl">
<menclose notation="madruwb">
12
</menclose>
</math>
|
|---|
階乗の引数は, 文字ラーム(ل)に似た形のもので包み込まれなければなりません. この記号は, 引数に適合するように両方向に引き伸ばされなければなりません. 新しいmenclose表記に対するmadruwbがこの場合に提案されています.
The argument to the factorial must be wrapped in a form similar to the
character LAM (ل), which must
be stretched in both directions to accommodate. A new menclose notation,
madruwb is proposed for this case.
形式
Style | 描画例
Image | MathML |
|---|
英語
English | ![[Image of binomial(5,12) in english style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arrangaen.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>(</mo><mtable><mtr><mtd>5</mtd></mtr><mtr><mtd>12</mtd></mtr></mtable><mo>)</mo>
</mrow>
</math>
|
|---|
アラビア語
Arabic | ![[image of binomial(5,12) in Arabic style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arranga.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block" dir="rtl">
<mmultiscripts><mo>ل</mo>
<mn>12</mn><none/>
<mprescripts/>
<none/><mn>5</mn>
</mmultiscripts>
</math>
|
|---|
最終的に, 積み上げられた分数はヨーロッパとアラビアの両方で同じ方法で描画されますが, RTLのアラビア語で斜線の分数は, 期待されたとおりに, RTLの順番の項を用いて現れるでしょう. すなわち, A割るBは"B/A"として現れます. 場所によっては, 優先されるのは, 斜線を鏡文字にして"B\A"(訳注:日本語フォントによっては半角バックスラッシュ\ではなく半角円記号¥が表示されます)とすることです. これらの場合に, 著者は, <mrow><mi>A</mi><mo>\</mo><mi>B</mi></mrow>のような逆の斜線\を用いる明瞭なマークアップを採用すべきです.
Finally, although stacked fractions are rendered the same way in both European and Arabic,
bevelled fractions in RTL Arabic will appear, as one would expect, with the terms in RTL order,
i.e. A divided by B would appear as "B/A".
In some locales, the preference is for the slash to also be mirrored, as "B\A". For these cases,
we suggest that authors employ explicit markup using the REVERSE SOLIDUS \, such as
<mrow><mi>A</mi><mo>\</mo><mi>B</mi></mrow>
.
3.5 ペルシア語
Persian
ペルシア語は一般に(RTLで書かれた)アラビア語を用いますが, モロッコ形式のように, LTRの数学の方向を用います. 1つの数学表記のみがペルシア語の書き方で特別なことが知られています. その表記は極限で用いられます.
Persian languages generally use the Arabic script (written RTL), but with
the mathematical directionality LTR, similar to the Moroccan style.
We are aware of only one mathematical notation unique to Persian writing, the notation used
for limits:
形式
Style | 描画例
Image | MathML |
|---|
英語
English | ![[Image of limit formula in English style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/limw.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<munder>
<mo movablelimits="false">lim</mo>
<mrow>
<mi>x</mi>
<mo>→</mo>
<mfrac bevelled="true">
<mi>π</mi>
<mn>10</mn>
</mfrac>
</mrow>
</munder>
<mo></mo>
<mrow>
<mi>sin</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mfrac>
<mn>1</mn>
<mn>4</mn>
</mfrac>
<mo></mo>
<mrow>
<mo>(</mo>
<msqrt>
<mn>5</mn>
</msqrt>
<mo>-</mo>
<mn>1</mn>
<mo>)</mo>
</mrow>
</mrow>
</mrow>
</math>
|
|---|
ペルシア語
Persian | ![[Image of limit formula in Persian style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/limf.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<munder>
<mo movablelimits="false">حد</mo>
<mrow>
<mi>x</mi>
<mo>→</mo>
<mfrac bevelled="true">
<mi>π</mi>
<mn>۱۰</mn>
</mfrac>
</mrow>
</munder>
<mo></mo>
<mrow>
<mi>sin</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mfrac>
<mn>۱</mn>
<mn>۴</mn>
</mfrac>
<mo></mo>
<mrow>
<mo>(</mo>
<msqrt>
<mn>۵</mn>
</msqrt>
<mo>-</mo>
<mn>۱</mn>
<mo>)</mo>
</mrow>
</mrow>
</mrow>
</math>
|
|---|
全ての表記がモロッコのモデル(LTR)に似ている一方, その表記は東アラビア・インド数字を用います. ("limit"に対する)言葉"حد"が使用されており, その言葉は, 字形の形成の影響のみ受けるべきですが, 下側添え字の長さに一致するよう水平方向に引き伸ばされるべきです.
While the overall notation is similar to the Moroccan model (LTR), it uses the
Eastern Arabic-Indic digits. The word "حد" (for "limit"), is
used; this word should not only be affected by glyph shaping,
but should be stretched horizontally to match the length of the underscript.
4 提案と明確化
Proposals and Clarifications
4.1 MathMLに対する双方向のアルゴリズムの明確化
Clarification of bidirectional Algorithm for MathML
下記は, どのように方向をMathMLに適用すべきか要約し, 特にどのように双方向のアルゴリズムを適用すべきか説明したものです(このことは, 種類HL4に属します. [ユニコードBiDi]第4.3節高い階層の通信規約: HL4を参照して下さい).
The following summarizes how directionality should be applied to MathML
and, in particular, describes how the bidirectional algorithm should be applied
(it falls into class HL4; See Higher Level
Protocols: HL4 in [UnicodeBiDi], section 4.3).
全ての数学の方向は, 一番外側のmath要素のltrまたはrtlのどちらか一方の値を取る(新しい)dir属性で決定すべきです. 既定値はltrです. この属性がrtlの場合, 全ての配置, 添え字, 極限, 表, 行列の配置は右から左へ進むべきです. このことは, 右から始まるmrootの無理数でも同じように影響があります 数学の方向がltrの場合, 配置は, 現在のMathML仕様書に適合すべきです.
The overall mathematical directionality should be determined by
a (new) dir attribute on the outermost math element
which takes one of the values ltr or rtl;
the default is ltr.
If this attribute is rtl the layout of all Layout, Script, Limit,
Table and Matrix schemata should proceed from right to left. This includes
such effects as the surd of an mroot starting from the right.
When the mathematical directionality is ltr, the layout should conform
to the current MathML specification.
各素子要素の文字の中身は, 分割された方向の断片として扱われ, 双方向のアルゴリズムが独立して各要素に適用されるべきです. 各素子要素の文字方向の初期値は, 数学の方向によって決められるべきです. この後者の性質は, 各鏡文字の記号が正確に取り扱われることを保証すべきです.
The text content of each Token element should be treated as a separate
directional segment and the bidirectional algorithm should be applied to each independently.
The initial directional context for each Token element is determined
by the mathematical directionality. This latter property should assure that
individual mirrored symbols are treated correctly.
例として, MathMLの断片について考えます.
As an example, consider the MathML fragment:
<mn>1</mn>
<mo>+</mo>
<mi>
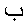 </mi>
<mo>-</mo>
<mn>2</mn>
</mi>
<mo>-</mo>
<mn>2</mn>
ブラウザによっては, 双方向のアルゴリズムをHTMLでのように式全体に間違って適用するでしょう. HTMLのアルゴリズムを適用すると, 最初の2つの項目はLTRに設定されますが, 文字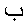 と出くわした後は, 方向を切り換えます. よって, 最後の3つの項目がひっくり返ります
と出くわした後は, 方向を切り換えます. よって, 最後の3つの項目がひっくり返ります
Some browsers mis-apply the bidirectional algorithm to the expression as a whole, as in HTML.
Applying the HTML algorithm would set the first two items LTR, but then switch directions upon
encountering the letter 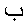 ;
thus the last three items are reversed.
;
thus the last three items are reversed.
形式
Style | 描画例
Image | MathML |
|---|
正しい
Right | ![[Image of expression rendered correctly]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/direction1.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display">
<mn>1</mn><mo>+</mo><mi>ب</mi><mo>-</mo><mn>2</mn>
</math>
|
|---|
間違い
Wrong | ![[Image of expression rendered incorrectly]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/direction2.png) | |
|---|
4.2 字形の形成
Glyph Shaping
字形の形成の決まりは, mtextの文字列の中身のみに適用するのではなく, (特にmiやmoの中の)数学記号として使われるアラビア語の文字列にも適用されます. この形成は, ひょっとすると積を表しているかもしれない記号の列から区分された単独の記号の視覚的な列です. このことは, 次の2つの例を区別するためにヨーロッパの数学でローマン体を利用することに類似しています.
Glyph shaping rules apply not only to the textual content of an mtext,
but also to Arabic character sequences used as mathematical symbols (particularly in
mi and mo). This shaping is the visual cue that
distinguishes a single symbol from a sequence of symbols, perhaps representing a product.
This is analogous to the use of roman font in European mathematics, to distinguish for example
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display"><mi>sin</mi></math>
と
from
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display"><mi>s</mi><mi>i</mi><mi>n</mi></math>
.
よって, 実装者は, 何らかの素子要素の文章の中身において, 各文字列に形成を適用すべきです.
Thus, implementors should apply shaping to each character sequence within the text content of
any token elements.
あるアラビア文字(ا د ذ ر ز و)は, 何も独特の語頭形または語中形を持っていません. 数学記号の中間でのそれらの利用は, 記号を2つの短い記号の積のように見せることになるでしょう. よって混乱を避けるため, 著者は, これらの文字を数学記号の中間で利用することを避けるべきです.
Certain Arabic characters (ا د ذ ر ز و)
have no unique initial or medial shapes. Their use in the middle of a mathematical symbol
would tend to make the symbol look like the product of two shorter symbols.
Thus, to avoid confusion, authors should avoid using these characters
in the middle of mathematical symbols.
4.3 追加の数学異体字
Additional Mathvariants
単独の文字の素子に対して, 太字やフラクタルの形式がヨーロッパの数学で用いられるように, 追加の形式が, 独立型と同様に, 利用可能な個別の記号の集合を拡大するために用いられます. アラビア語の数学で用いられる書式は, 個々の文字に適用される"語頭"形に加えて, "テール付き", "ループ付き", "縦長"です. さらに, "二重線"形式が一般に用いられます. 次に示す表は, 様々な形式の文字ジームを示しており, 点付きと点無しの両方の形式(下記参照)で示しています.
For single character tokens, additional styles, besides isolated, are used
to enlarge the set of available distinct symbols, just as the bold and Fraktur styles are
used in European mathematics. The styles used in Arabic mathematics
are "tailed", "looped" and "stretched", in addition to the "initial" style applied to
the individual character. Furthermore, the "double-struck" style is commonly used.
The following table shows the character JEEM in the various styles, in both
dotted and undotted forms (see below):
| 独立形
isolated | 語頭形
initial | テール付き
tailed | ループ付き
looped | 縦長
stretched | 二重線
double-struck |
|---|
点付き
dotted | 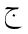 | 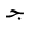 | 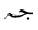 | 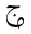 | 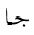 |  |
|---|
点無し
undotted | 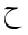 | 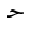 | 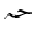 | 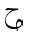 | 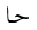 |  |
|---|
アラビア語に適用するときは, 字形の形成の結果, 特に単独の文字の要素に対する"独立形"を表すために, mathvariantを "normal"と見なすことが推奨されています. また, mathvariantに次に示す値, "initial", "tailed", "looped" and "stretched"を加えることが提案されています.
It is proposed to consider the mathvariant "normal",
when applied to Arabic, to mean the result of glyph shaping, and in particular,
the "isolated" style for single character tokens. It is also proposed to
add the following values allowed for mathvariant:
"initial", "tailed", "looped" and "stretched".
"bold", "italic", "fraktur", "script", "sans-serif", "monospace"の数学用異体字(またはそれらを組合せたもの)をアラビア語に適用することは, ("bold"と"italic"を認めるとの意見もあるものの)意味がないとされています. そしてまた, 適用される字形の形成を受けるべき複数文字の素子に"normal"以外の何らかの数学用異体字を適用することも意味がないです. 現在のMathML仕様書は, 明瞭な解釈をもつ文字の統合や数学用異体字のみが追加多言語面の数学用英数字記号に一致するものであることを指し示しています. 類似した論争が, アラビア語や提案されている(まだユニコードの一部でない)アラビア語の数学用英数字記号[ユニコード提案]に対しても起こります.
It is not expected to be meaningful to apply the "bold", "italic", "fraktur", "script",
"sans-serif" or "monospace" mathvariants (or combinations) to Arabic (although there is some
sentiment for allowing "bold" and "italic"). Nor is it meaningful to apply any mathvariant
other than "normal" to multicharacter tokens, which should have glyph shaping applied.
The current MathML specification points out that the only combinations of characters and
mathvariant that have an unambiguous interpretation are those that correspond to the
SMP Math Alphanumeric Symbols. An analogous argument is to be made for Arabic and the proposed
Arabic Math Alphabetic Symbols [UnicodeProposition] (not yet part of Unicode).
点付きと点無し両方の英数字記号がこのメモの中で出てきます. どちらの型を用いるかを選ぶのは, 地域の好みによります. ただし, 文書は, 点付きか点無しかどちらの記号を使用し, 混ぜて使用することはなく, 特に点は意味の区別を示すのには使われません. よって, 点を付けることが数学用異体字の値の適切な候補とは感じられず, むしろ, 利用者のブラウザで利用可能な記号のフォントの選択やひょっとしたらCSSを通した選択によって対応させるべきです.
Both dotted and undotted alphabetic symbols are encountered in this Note.
The choice of which type to use is up to local preferences, however; documents use
either dotted or undotted symbols, but not a mixture, and in particular, the dots are not used
to indicate semantic distinctions. Thus, it is not felt that dotting is a good
candidate for a mathvariant value, but rather should be accommodated by the choice of
symbol fonts available to user's browser, or possibly through CSS.
4.4 鏡文字
Mirroring
MathMLの属性lspace, rspace, lquote, rquoteは, 厳密に左と右ではなく, 開始と終了として解釈されるべきです. この歴史的な例外は, かっこに対する標準のユニコード名に類似しています. LEFT PARENTHESISとRIGHT PARENTHESISは, mirroredとして記述され, それぞれOPENING PARENTHESIS, CLOSING PARENTHESISを表すのに必要とされます.
The MathML attributes lspace, rspace,
lquote and rquote should be interpreted as opening and closing,
rather than strictly left and right. This historical anomaly is analogous to
the standard Unicode names for the parentheses:
The LEFT PARENTHESIS and RIGHT PARENTHESIS
are marked as mirrored and are taken to represent
OPENING PARENTHESIS and CLOSING PARENTHESIS, respectively.
数学作業部会と関連する部会は, アラビア語の数学に必要なコードポイントが利用できるだけでなく, 適切に鏡文字のために記述されることを確かなものにするために作業すべきです. 利用可能なフォントが利用できるようになり, 鏡文字に関連する筆記体の品質を重視することが望まれています.
The Math Working Group, and other interested parties, should work to assure
that the necessary codepoints for Arabic mathematics are not only available, but
appropriately marked for mirroring.
It is also to be hoped that available fonts will be available, and will
respect the calligraphic qualities regarding mirroring.
4.5 水平方向に引き伸ばす
Horizontal Stretchiness
アラビア語の数学において, 総和, 総積, 極限は, それらが適用される(上または下の)範囲と同じ幅まで, 水平方向に引き伸ばされます. そのように引き伸ばすことは, ヨーロッパの数学ではときどき起こりますが, 稀です. MathMLの水平方向に引き伸ばす際の決まり([MathML22e] 第3.2.5.8.3節)で, 標準の仕様書は, 描画ソフトウェアの裁量でそのように記号を水平方向に引き伸ばすことを認めています. このメモでは, 単に開発者に, 適切なアラビア語の記号にこの機能を実装することを促しています.
In Arabic mathematics, the sum, product and limit are commonly stretched horizontally
to the same width as the limits (over or under) that apply to them. Such stretching
does occasionally appear, but is rare, in European mathematics.
In Horizontal
Stretching Rules of MathML
([MathML22e] section 3.2.5.8.3), standard allows for such horizontal stretching
of some symbols at the discretion of the rendering agent. In this Note, we
simply encourage developers to implement this feature for the appropriate Arabic symbols.
4.6 追加の構造
Additional Constructs
階乗のアラビア語表記は, 囲いの一種です. 追加の値madruwb(階乗に対するアラビア語のمضروبの英語表記)をmencloseのnotation属性に追加することを提案しています.
The Arabic notation for factorial is a sort of enclosure.
We propose to add an additional allowed value madruwb (transliteration
of the Arabic مضروب for factorial) for
the notation attribute of menclose.
5 結論と将来の作業
Conclusions and Future Work
このメモは, 数学をアラビア語や他のRTL言語で表現するときに直面する課題について, 特に, それらの表記がMathML2で説明されたモデルとどのように異なるかに焦点を当てて説明しています. 私達の知る限りでは, ここで説明された独特の表記は, 全て既知の違いについて説明していました.
This Note describes the notational issues encountered in presenting
mathematics within Arabic and other RTL languages, in particular focusing on
how these notations differ from the model described by MathML2. To the best of
our knowledge, the unique notations described here cover all known differences.
このメモは, MathML仕様書の将来の改訂で考慮される改善点についても提案しています. それらの改善点は, 数学をアラビア語の文書にうまい具合に組みいれるのに, アラビア語を話す著者に慣例的に利用される形式でプレゼンテーションMathMLを使用することを認めるでしょう.
This Note also proposes enhancements to be considered in a future revision
of the MathML specification. These enhancements would allow Presentation MathML to be
used to conveniently incorporate mathematics into Arabic documents in a style
conventionally used by Arabic speaking authors.
アラビア語の文章における数学の上手くいった利用方法には, ここで提案した拡張に加えて, 適切なコードポイントがユニコードに含まれていることや, それらのコードポイントが鏡文字として正確に記述されていることも必要としてします. 提案([ユニコード提案],[アラビア数学ユニコード])の中には, 既に実現されているものもあります.
The successful use of mathematics in Arabic texts will also require,
in addition to the extensions proposed here, that the appropriate codepoints
are included in Unicode, and that those codepoints are correctly marked as
mirrored. Some proposals ([UnicodeProposition],[ArabicMathUnicode]) have already been made.
6 謝辞
Acknowledgments
この文書は, 数学関連部会のメンバーによって生み出されました. この関連部会の議長は, David Carlisle (外部の専門家)とRobert Miner (Design Science社)です. 作業部会のメンバーは, (執筆時点で)Isam Ayoubi (外部の専門家), Laurent Bernardin (Waterloo Maple社), Stephane Dalmas (フランス国立情報学自動制御研究所), Stan Devitt (外部の専門家), Max Froumentin (W3C), Patrick D F Ion (外部の専門家), Azzeddine LAZREK (外部の専門家), Paul Libbrecht (ドイツ人工知能研究センター), Manolis Mavrikis (エディンバラ大学), Bruce Miller (アメリカ国立標準技術研究所), Luca Padovani (ボローニャ大学), Neil Soiffer (Design Science社), Stephen Watt (Waterloo Maple社)です.
This document has been produced by the members of the Math Interest
Group. The chairs of this Interest Group are David Carlisle (invited
expert) and Robert Miner (Design Science, Inc.). Other members of the
Working Group are (at the time of writing): Isam Ayoubi (invited
expert), Laurent Bernardin (Waterloo Maple Inc.), Stephane Dalmas
(Institut National de Recherche en Informatique et en Automatique),
Stan Devitt (invited expert), Max Froumentin (W3C), Patrick D F Ion
(invited expert), Azzeddine LAZREK (invited expert), Paul Libbrecht
(German Research Center for Artificial Intelligence), Manolis Mavrikis
(University of Edinburgh), Bruce Miller (National Institute of
Standards and Technology), Luca Padovani (University of Bologna), Neil
Soiffer (Design Science, Inc.), Stephen Watt (Waterloo Maple Inc.)
編集者は, このメモの執筆を先導する連絡を行い, このメモの草案にたくさんの建設的な意見を述べたRichard Ishidaにも喜んで感謝します.
The editors would also like to thank Richard Ishida for initiating
the contacts that lead to the writing of this Note, and for many
constructive comments on a draft of it.
7 奥付
Production Notes
アラビア語やペルシア語の数式の描画例は, RyDArabシステム[RyDArab]とFarsiTeXシステム[FarsiTeX]をそれぞれ利用して組み立てられました.
The images of Arabic and Persian expressions were composed using the RyDArab
system [RyDArab], and the FarsiTeX system [FarsiTeX], respectively.
![[Arabic Script samples]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/khtout.png)
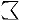 は, 例えば, シグマ
は, 例えば, シグマ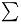 の単純な鏡文字
の単純な鏡文字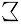 ではありません.
ではありません.![[Image of Arabic-Indic Digits]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arind.png)
![[Image of Eastern Arabic-Indic Digits]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/esarind.png)
![[Image of formula in English style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/expren.png)
![[Image of formula in French style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfr.png)
![[Image of formula in Moroccan style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfrm.png)
![[Image of simplified formula in Moroccan style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprfrn.png)
![[Image of formula in Maghreb style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprare.png)
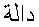 = "function"の頭文字である)ダール
= "function"の頭文字である)ダール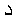 , アラビア文字バー
, アラビア文字バー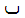 , そして(点無しの)正接に対する関数名を省略した文字
, そして(点無しの)正接に対する関数名を省略した文字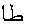 . そのうえ, これらの違いは, 地域対応の範疇に分類されますが, ユニコードの双方向のアルゴリズムは, 字形の形成に従って素子要素に個別に適用すべきという意見を補強しています.
. そのうえ, これらの違いは, 地域対応の範疇に分類されますが, ユニコードの双方向のアルゴリズムは, 字形の形成に従って素子要素に個別に適用すべきという意見を補強しています.![[Image of formula in Machrek style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/exprarw.png)
 は, (アラビア語の
は, (アラビア語の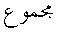 = "sum"の頭文字であり)総和に用いられています. 別の文字
= "sum"の頭文字であり)総和に用いられています. 別の文字 は, (アラビア語の"関数"
は, (アラビア語の"関数" の頭文字であり)関数に用いられています. 初等関数の名前を省略した文字
の頭文字であり)関数に用いられています. 初等関数の名前を省略した文字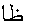 は, 点を持ちます. そして, 数字の形式は, アラビア・インド数字を使用し, 数字の区切りに対してはコンマを使用します(ただし, 文章で使われるアラビア語のコンマと同じではありません).
は, 点を持ちます. そして, 数字の形式は, アラビア・インド数字を使用し, 数字の区切りに対してはコンマを使用します(ただし, 文章で使われるアラビア語のコンマと同じではありません).![[Image of 12 factorial in english style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/drbcen.png)
![[Image of 12 factorial in Arabic style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/drbc.png)
![[Image of binomial(5,12) in english style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arrangaen.png)
![[image of binomial(5,12) in Arabic style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/arranga.png)
![[Image of limit formula in English style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/limw.png)
![[Image of limit formula in Persian style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/limf.png)
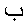 </mi>
<mo>-</mo>
<mn>2</mn>
</mi>
<mo>-</mo>
<mn>2</mn>
![[Image of expression rendered correctly]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/direction1.png)
![[Image of expression rendered incorrectly]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/direction2.png)
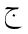
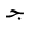
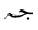
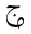
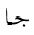

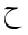
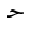
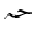
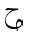
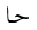

![[Image of literal summation]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/mgmuec.png) と
と![[Image of symbolic summation]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/mgmues.png) です.
です.![[Image of literal product]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/gdaac.png) と
と![[Image of symbolic product]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/gdaas.png) です.
です.![[Image of literal limit]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/nhaytc.png) と
と![[Image of limit in Persian style]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/nhaytf.png) です. 後者はペルシア語で使われる表記です.
です. 後者はペルシア語で使われる表記です.![[Image of poorly stretched summation]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/mgmuel.png)
![[Image of poorly stretched product]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/gdaal.png)
![[Image of poorly stretched limit]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/nhaytl.png)
![[Image of poorly stretched factorial]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/drbl.png)
![[Image of stretched summation]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/mgmuegl.png) と
と![[Image of stretched product]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/gdaagl.png) のようにヨーロッパでは稀です. これらの伸長は, アラビア語の数学では
のようにヨーロッパでは稀です. これらの伸長は, アラビア語の数学では![[Image of stretched mirrored summation]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/mgmuega.png) と
と![[Image of stretched mirrored product]](https://www.w3.org/TR/2006/NOTE-arabic-math-20060131/arabic-images/gdaaga.png) のようにより一般的で, より望まれています.
のようにより一般的で, より望まれています.