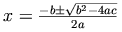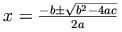1 導入
Introduction

1.1 数学とその表記
Mathematics and its Notation

数学の確立された機能は, 複雑で高度に発展した2次元の記号の表記の利用です. J. R. Pierce氏が彼のコミュニケーション理論の著書で書いたように, 数学とその表記は, 1つの同じものと見なされるべきではありません[Pierce1961]. 数学の考えは, その考えを表現する表記と独立して存在できます. しかしながら, 意味と表記の間の関係は微妙で, 数学の説明したり解析したりする能力の一部は, 記号の形式で考えを表現したり巧みに扱ったりする可能性に起源を持ちます. インターネットで数学を利用可能にする際の, 数学用マークアップ言語(MathML)登場以前の課題は, 書いたり, 印刷したりする数学の高度に発展した表記や, 電子媒体での相互連絡の新しい潜在能力を, 文書で利用できる場合に, 表記と内容(つまり, その意味)を捉えることです.

A distinguishing feature of mathematics is the use of a complex and highly evolved system of two-dimensional symbolic notation. As J. R. Pierce writes in his book on communication theory, mathematics and its notation should not be viewed as one and the same thing [Pierce1961]. Mathematical ideas can exist independently of the notation that represents them. However, the relation between meaning and notation is subtle, and part of the power of mathematics to describe and analyze derives from its ability to represent and manipulate ideas in symbolic form. The challenge before a Mathematical Markup Language (MathML) in enabling mathematics on the World Wide Web is to capture both notation and content (that is, its meaning) in such a way that documents can utilize the highly evolved notation of written and printed mathematics as well as the new potential for interconnectivity in electronic media.

数学表記は, 絶えず人々が考えを深めたり, 発表したりする方法を刷新し続けることを推し進めています. 算術共通の表記でさえ, その時代を引っ張ってきた数学者により支持された, たくさんの現存しない表記を含め, 驚くほど様々な書式を経てきました[Cajori1928]. 現在の数学表記は, 何世紀にも渡る洗練の成果で, 高品質の植字に対する表記の慣習はとても複雑で微妙です. 例えば, 数学を表す変数や文字は, 普通, 現在では, 通常の斜体とは別個の特別な数学用の斜体の字形です. このことは, 16世紀後半のヨーロッパで導入されたとみられています. +, -, ×, /といった演算子記号の周りの間隔は, 何世紀にも渡って発展してきた演算子の優先度についての慣習を反映して, 文章での間隔とはわずかに異なります. 上付き文字や下付き文字の位置揃えから, かっこの大きさの決まり, 数学の分野ごとの特別な表記の習慣についてまで, 数学の植字の慣習に, たくさんの本が取り組んできました. 現在のコンピュータによる植字や組版システムの微妙な細部について説明したマニュアルは, 何百ものページになるでしょう.

Mathematical notation evolves constantly as people continue to innovate in ways of approaching and expressing ideas. Even the common notation of arithmetic has gone through an amazing variety of styles, including many defunct ones advocated by leading mathematical figures of their day [Cajori1928]. Modern mathematical notation is the product of centuries of refinement, and the notational conventions for high-quality typesetting are quite complicated and subtle. For example, variables and letters which stand for numbers are usually typeset today in a special mathematical italic font subtly distinct from the usual text italic; this seems to have been introduced in Europe in the late sixteenth century. Spacing around symbols for operations such as +, -, × and / is slightly different from that of text, to reflect conventions about operator precedence that have evolved over centuries. Entire books have been devoted to the conventions of mathematical typesetting, from the alignment of superscripts and subscripts, to rules for choosing parenthesis sizes, and on to specialized notational practices for subfields of mathematics. The manuals describing the nuances of present-day computer typesetting and composition systems can run to hundreds of pages.

数学や一般に印刷された文章における表記の慣習は, 視線を誘導したり, 印刷された式を読んだり理解したりするのをとても容易にしたりします. 普段, 当たり前のように思っていますが, 私たちは現代の読者として, 段落, 大文字, フォントの種類や状態, この文書で使われているような節への少数のような番号付けといった数々の慣習に頼っています. そのような表記の慣習は, 画面で読むことの難しさと向き合っている電子媒体では, ひょっとしたらより重要でさえあるかもしれません. コンピュータに関連した適切な標準は, 印刷の世界を超えて数学に触れる機会を広げることを可能にします. 単にインターネットの以前の利用での数学を記述する方法としては, 重点的にTEX(TeXとも書く)[Knuth1986]を含んだ卓越した方法やSGML([AAP-math], [Poppelier1992], [ISO-12083])に基づいた手段が挙げられました.

Notational conventions in mathematics, and in printed text in general, guide the eye and make printed expressions much easier to read and understand. Though we usually take them for granted, we, as modern readers, rely on numerous conventions such as paragraphs, capital letters, font families and cases, and even the device of decimal-like numbering of sections such as is used in this document. Such notational conventions are perhaps even more important for electronic media, where one must contend with the difficulties of on-screen reading. Appropriate standards coupled with computers enable a broadening of access to mathematics beyond the world of print. The markup methods for mathematics in use just before the Web rose to prominence importantly included TEX (also written TeX) [Knuth1986] and approaches based on SGML ([AAP-math], [Poppelier1992] and [ISO-12083]).

どのように広範囲に渡る数学表記の現在の慣習が出来上がってきたかは注目すべき点です. 一般的な2次元の配置やほとんどの同じ記号が, 関係者がヨーロッパであれば左から右の, 中東であれば右から左の, 全ての現在の数学コミュニケーションで使われています. もちろん, 使われている記号の慣習, 特に名付けられた関数や変数は, 地域の言語や文字を使用しがちかもしれません. ほとんどの共通のものの中で最も大きな違いは, 一部のアラビア語圏で利用される, 完全に数学表記を右から左に, 大雑把に言うとヨーロッパの伝統の鏡のように配置する形式です.

It is remarkable how widespread the current conventions of mathematical notation have become. The general two-dimensional layout, and most of the same symbols, are used in all modern mathematical communications, whether the participants are, say, European, writing left-to-right, or Middle-Eastern, writing right-to-left. Of course, conventions for the symbols used, particularly those naming functions and variables, may tend to favor a local language and script. The largest variation from the most common is a form used in some Arabic-speaking communities which lays out the entire mathematical notation from right-to-left, roughly in mirror image of the European tradition.

しかしながら. インターネット上で数学を扱ことは, 単にウェブブラウザで伝統的な数学表記を表示する方法を探すことより大事です. インターネットは, 知識の保管庫のような土台になる基本的な変化や相互接続性が中心的な役割を担うような変化を示しています. 自動処理, 検索, 索引付けを促進し, 他の数学の応用や文脈で再利用できる, 数学で意思疎通を取る方法を見つけることが重要になってきています. 情報技術の進歩に伴い, 私達が表現したり, コード化したり, 最終的に私達の数学の洞察や相互理解を深める可能性が広がる機会ができてきています. 私達は, 後で仕様を示すMathMLがインターネットでの数学の開発における重要な一歩になると信じています.

However, there is more to putting mathematics on the Web than merely finding ways of displaying traditional mathematical notation in a Web browser. The Web represents a fundamental change in the underlying metaphor for knowledge storage, a change in which interconnection plays a central role. It has become important to find ways of communicating mathematics which facilitate automatic processing, searching and indexing, and reuse in other mathematical applications and contexts. With this advance in communication technology, there is an opportunity to expand our ability to represent, encode, and ultimately to communicate our mathematical insights and understanding with each other. We believe that MathML as specified below is an important step in developing mathematics on the Web.

1.2 起源と目標
Origins and Goals

1.3 概要
Overview

MathMLは, 数学を記述するためのマークアップ言語です. HTMLや他の構文も利用できますが, MathMLは通常XML構文で表現されます. MathMLの特別な側面として, マークアップの2つの系統があります. 第3章 プレゼンテーションマークアップで説明されているプレゼンテーションマークアップは, 数式を表示するために利用されます. また, 第4章 コンテントマークアップで説明されているコンテントマークアップは, 数学の意味を伝えるために利用されます. コンテントマークアップは特定の細部について指定されています. この仕様書は, コンテント辞書と呼ばれるXML形式を用います. この形式はOpenMath協会によって開発されてきており, OpenMath協会とW3C数学作業部会との共同開発による, この仕様書で利用される辞書[OpenMath2004]です.

MathML is a markup language for describing mathematics. It is usually expressed in XML syntax, although HTML and other syntaxes are possible. A special aspect of MathML is that there are two main strains of markup: Presentation markup, discussed in Chapter 3 Presentation Markup, is used to display mathematical expressions; and Content markup, discussed in Chapter 4 Content Markup, is used to convey mathematical meaning. Content markup is specified in particular detail. This specification makes use of an XML format called Content Dictionaries This format has been developed by the OpenMath Society, [OpenMath2004] with the dictionaries being used by this specification involving joint development by the OpenMath Society and the W3C Math Working Group.

両方のマークアップの系統に共通する基礎については, 第2章 MathMLの基礎で網羅しています. 単独のMathMLの例に対する, これらのマークアップの混在の意味や外部のマークアップは, 第5章 数式に対するマークアップ言語の混在で説明しています. MathMLが様々な応用の手法とどのように相互作用するかについて, 第6章 ホスト環境との相互作用で網羅しています. 最後に, 特別な記号についての議論や文字, 実体, 書式に関連する問題について, 第7章 文字, 実体, 書式で示しています.

Fundamentals common to both strains of markup are covered in Chapter 2 MathML Fundamentals, while the means for combining these strains, as well as external markup, into single MathML objects are discussed in Chapter 5 Mixing Markup Languages for Mathematical Expressions. How MathML interacts with applications is covered in Chapter 6 Interactions with the Host Environment. Finally, a discussion of special symbols, and issues regarding characters, entities and fonts, is given in Chapter 7 Characters, Entities and Fonts.

1.4 最初の例
A First Example

2次方程式の解の公式は単純ですが, MathMLマークアップの教育的な例を提供します.

The quadratic formula provides a simple but instructive illustration of MathML markup.

MathMLは, この数式に対する2つの雰囲気のマークアップを提供します. 1つ目は, 数式の実際の表現, 記号を調整した2次元の配置に力を入れています. この形式の例をすぐ下に示します. 2つ目のものは, 数学の内容に力を入れており, 1つ目のものの後に例を示します.

MathML offers two flavors of markup of this formula. The first is the style which emphasizes the actual presentation of a formula, the two-dimensional layout in which the symbols are arranged. An example of this type is given just below. The second flavor emphasizes the mathematical content and an example of it follows the first one.

<mrow>
  <mi>x</mi>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mrow>
        <mo>-</mo>
        <mi>b</mi>
      </mrow>
      <mo>&#xB1;<!--PLUS-MINUS SIGN--></mo>
      <msqrt>
        <mrow>
          <msup>
            <mi>b</mi>
            <mn>2</mn>
          </msup>
          <mo>-</mo>
          <mrow>
            <mn>4</mn>
            <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
            <mi>a</mi>
            <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
            <mi>c</mi>
          </mrow>
        </mrow>
      </msqrt>
    </mrow>
    <mrow>
      <mn>2</mn>
      <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
      <mi>a</mi>
    </mrow>
  </mfrac>
</mrow>

この数式における上付き文字2について考えます. その文字は, ここでは二乗の演算を表していますが, 他の状況での上付き文字は文脈に依存します. 上付き文字を伴う文字は, ベクトルの特定の要素を表すのに使うことができます. もしかすると, 上付き文字は何らかの構造の違う形式を番号付けしているのかもしれません. 同様に, 単に他の文字の後ろに書かれている2つの文字は, 解の公式の中にある場合は, 一緒に掛けられている2つの変数を表していますが, それらは, 単独の変数の名前を作り上げている2つの文字かもしれません. MathMLでコンテントマークアップと呼ばれているものは, たくさんの共通の数式のより精密は数学の意味を表しています. このマークアップの形式で示される解の公式は次のとおりです.

Consider the superscript 2 in this formula. It represents the squaring operation here, but the meaning of a superscript in other situations depends on the context. A letter with a superscript can be used to signify a particular component of a vector, or maybe the superscript just labels a different type of some structure. Similarly two letters written one just after the other could signify two variables multiplied together, as they do in the quadratic formula, or they could be two letters making up the name of a single variable. What is called Content Markup in MathML allows closer specification of the mathematical meaning of many common formulas. The quadratic formula given in this style of markup is as follows.

<apply>
  <eq/>
  <ci>x</ci>
  <apply>
    <divide/>
    <apply>
      <plus/>
      <apply>
        <minus/>
        <ci>b</ci>
      </apply>
      <apply>
        <root/>
        <apply>
          <minus/>
          <apply>
            <power/>
            <ci>b</ci>
            <cn>2</cn>
          </apply>
          <apply>
            <times/>
            <cn>4</cn>
            <ci>a</ci>
            <ci>c</ci>
          </apply>
        </apply>
      </apply>
    </apply>
    <apply>
      <times/>
      <cn>2</cn>
      <ci>a</ci>
    </apply>
  </apply>
</apply>