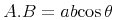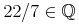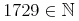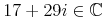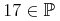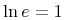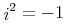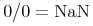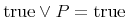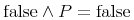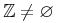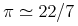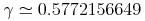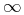4.1 導入
Introduction
4.1.1 コンテントマークアップの意図
The Intent of Content Markup
コンテントマークアップの意図は, 式に対する何らかの特定の描画ではなく, 式の基本的な数学的意味の明確なコード化を提供することです. 数学は, 数学的概念を定義し解析するための厳格で整然とした議論の利用と, その概念を表現し伝えるための(比較的)整然とした表記体系の利用の両方によって成り立っています. しかしながら, 数学とその表記を, 1つの同じものとして見るべきではありません. 数学表記は, 自然言語より論理的であるにも関わらず, 時として, あいまいで, 文脈に依存し, 分野ごとに変化します. 場合によっては, 発見的手法は, 数学表記から数学的意味を十分に推測するかもしれません. しかし, その他の多くの場合に, 基本となる整然とした数学事象に直接働きかけることが好まれます. コンテントマークアップは, 論理的で拡張可能な意味の枠組とその目的のためのマークアップ言語を提供します.
The intent of Content Markup is to provide an explicit encoding of the underlying mathematical meaning of an expression, rather than any particular rendering for the expression. Mathematics is distinguished both by its use of rigorous formal logic to define and analyze mathematical concepts, and by the use of a (relatively) formal notational system to represent and communicate those concepts. However, mathematics and its presentation should not be viewed as one and the same thing. Mathematical notation, though more rigorous than natural language, is nonetheless at times ambiguous, context-dependent, and varies from community to community. In some cases, heuristics may adequately infer mathematical semantics from mathematical notation. But in many others cases, it is preferable to work directly with the underlying, formal, mathematical objects. Content Markup provides a rigorous, extensible semantic framework and a markup language for this purpose.
表現から意味を推測する困難さは, 表現から意味への紐付けや逆の紐付けが1つより多くあるという事実に起因します. 例えば, "Hをeで乗じる"という数学の構造は, 明確な演算子を用いてH × eという具合によくコード化されます. 異なる表現の文脈では, 掛け算の記号が見えない"H e"が用いられたり, 話し言葉"掛ける"を用いて表されたりするかもしれません. 一般に, たくさんの異なった表現が, 文脈や, 著者または読者の書式の好みによって利用できます. つまり, 文脈の外で"H e"が与えられるとき, それが化学物質の名前なのか, 2つの変数Hとeの数学の積なのか決めることは困難でしょう. 数学表現は, 文化や地理的な地域によっても変化します. 例えば, 筆算の割り算に対するたくさんの表記が, 現在世界の様々な所で利用されています. 例えば, 最大と最小を表す音楽のシャープとフラット記号の利用[Chaundy1954]のように, 表記は使われなくなることもあるでしょう. 上で述べた掛け算の1644年に使われていた表記は Heでした[Cajori1928].
Heでした[Cajori1928].
The difficulties in inferring semantics from a presentation stem
from the fact that there are many to one mappings from presentation to
semantics and vice versa. For example the mathematical construct
"H multiplied by e" is often
encoded using an explicit operator as in
H × e. In different
presentational contexts, the multiplication operator might be
invisible "H e", or rendered
as the spoken word "times". Generally, many different
presentations are possible depending on the context and style
preferences of the author or reader. Thus, given
"H e" out of context it may be
impossible to decide if this is the name of a chemical or a
mathematical product of two variables H and
e. Mathematical presentation also varies across cultures
and geographical regions. For example, many notations for long
division are in use in different parts of the world today. Notations
may lose currency, for example the use of musical sharp and flat
symbols to denote maxima and minima [Chaundy1954]. A
notation in use in 1644 for the multiplication mentioned above was
 He [Cajori1928].
He [Cajori1928].
聴覚的または視覚的にどう表されるかを尊重せずに, 基本となる数学的構造を明確にコード化することで, 数学事象を意味的に処理するシステム間で, より正確な情報を交換することが可能です. 上のありふれた例では, そのようなシステムは, 変数Hとeに値を代入し, 計算結果を求めることが可能でしょう. 重要な応用分野は, 数式処理システム, 自動推論システム, 産業や科学での応用, 多言語の翻訳システム, 数学の研究, 対話方式の教科書を含みます.
By encoding the underlying mathematical structure explicitly, without regard to how it is presented aurally or visually, it is possible to interchange information more precisely between systems that semantically process mathematical objects. In the trivial example above, such a system could substitute values for the variables H and e and evaluate the result. Important application areas include computer algebra systems, automatic reasoning system, industrial and scientific applications, multi-lingual translation systems, mathematical search, and interactive textbooks.
この章の構成は次のとおりです. 第4.2節 式の構造をコード化するコンテントMathML要素では, 厳格なコンテントマークアップを構成する核となる要素の集合について説明します. 厳格なコンテントマークアップは, 一般的な式のツリー構造を有意義な論理的方法でコード化するのに十分です. それらは, 1対1でOpenMath要素の集合と対応します. OpenMathは, 拡張可能なコンテント辞書の利用を通して, 整然とした数学事象や意味を表現する標準です. 厳格なコンテントマークアップは, 正確な数学的意味と式のツリー構造を, OpenMathのコンテント辞書を参照することで結び付ける仕組みを定義しています. 次の2つの節は, 厳格なコンテントマークアップより目的によっては便利な, よりくだけた語彙の多いマークアップを導入します. 第4.3節 具体的な構造に対するコンテントMathMLでは, 積分や総和や総積の極限といった, 少ない数の数学用語を表現するマークアップを導入します. それらの構造は, おそらく厳格なコンテントマークアップの式として書き換えられ, 書き換えの決まりについても示します. 第4.4節 具体的な演算子と定数に対するコンテントMathMLでは, 一般的な関数, 演算子, 定数に対する要素を導入します. この節は, 同じ意味の厳格なコンテントマークアップの式を含め, たくさんの例を含んでいます. 第4.5節 非推奨のコンテント要素では, MathML1と2からの要素で現在は利用が推奨されないものを一覧にしています. 最後に, 第4.6節 厳格なコンテントMathMLへの変換は, 任意のコンテントマークアップを厳格なコンテントマークアップに変換するアルゴリズムを要約しています. 章の残りの部分を通して導入した一連の全ての書き換えの決まりをまとめています.
The organization of this chapter is as follows. In Section 4.2 Content MathML Elements Encoding Expression Structure, a core collection of elements comprising Strict Content Markup are described. Strict Content Markup is sufficient to encode general expression trees in a semantically rigorous way. It is in one-to-one correspondence with OpenMath element set. OpenMath is a standard for representing formal mathematical objects and semantics through the use of extensible Content Dictionaries. Strict Content Markup defines a mechanism for associating precise mathematical semantics with expression trees by referencing OpenMath Content Dictionaries. The next two sections introduce markup that is more convenient than Strict markup for some purposes, somewhat less formal and verbose. In Section 4.3 Content MathML for Specific Structures, markup is introduced for representing a small number of mathematical idioms, such as limits on integrals, sums and product. These constructs may all be rewritten as Strict Content Markup expressions, and rules for doing so are given. In Section 4.4 Content MathML for Specific Operators and Constants, elements are introduced for many common function, operators and constants. This section contains many examples, including equivalent Strict Content expressions. In Section 4.5 Deprecated Content Elements, elements from MathML 1 and 2 whose use is now discouraged are listed. Finally, Section 4.6 The Strict Content MathML Transformation summarizes the algorithm for translating arbitrary Content Markup into Strict Content Markup. It collects together in sequence all the rewrite rules introduced throughout the rest of the chapter.
4.1.2 コンテントMathMLの式の構造と範囲
The Structure and Scope of Content MathML Expressions
コンテントMathMLは, 式のツリー構造として数学事象を表現します. 一般的な式のツリー構造を構成する概念としては, 例えば, 演算子を変数などに適用することです. 例えば, 和"x+y"は, 足し算の演算子を2つの引数xとyに適用するものと考えることができます. また, 式"cos(π)"は, 余弦関数を数πに適用するものと考えられます.
Content MathML represents mathematical objects as expression trees. The notion of constructing a general expression tree is e.g. that of applying an operator to sub-objects. For example, the sum "x+y" can be thought of as an application of the addition operator to two arguments x and y. And the expression "cos(π)" as the application of the cosine function to the number π.
一般的な決まりとして, ツリー構造の末端の要素は, 数字, 変数, 四則演算子などの基本となる数学の対象物です. ツリー構造の中間の要素は, 関数の適用や複合したものを組み立てる他の数学の構造を表します. 関数の適用は, 最も重要な例を提供します. 中間の要素は, その引数自身が中間の要素の下の要素によって表される関数かもしれない, いくつかの引数への関数の適用を表すものもあるでしょう.
As a general rule, the terminal nodes in the tree represent basic mathematical objects such as numbers, variables, arithmetic operations and so on. The internal nodes in the tree represent function application or other mathematical constructions that build up a compound objects. Function application provides the most important example; an internal node might represent the application of a function to several arguments, which are themselves represented by the nodes underneath the internal node.
一般的な数式の意味は, 意見が合致する問題ではありません. 数学のほとんどを体系的にコード化することは, 膨大な作業となるでしょう. その作業は完了することはないでしょう. その代わり, MathMLは, 膨大な数の応用事例の中から十分なように注意深く選んだ, 比較的小さな数のごく普通の数学的構造を明確にしています. 加えて, MathMLは, 基本的な集合の外にある数学的概念を, それらを適切に表現することを認めることで, 参照する仕組みを提供しています.
The semantics of general mathematical expressions is not a matter of consensus. It would be an enormous job to systematically codify most of mathematics – a task that can never be complete. Instead, MathML makes explicit a relatively small number of commonplace mathematical constructs, chosen carefully to be sufficient in a large number of applications. In addition, it provides a mechanism for referring to mathematical concepts outside of the base collection, allowing them to be represented, as well.
コンテント要素の基本的な集合は, アメリカ合衆国の幼稚園から高校まで利用する, 場合によってはさらに大学の最初の2年間を通じて利用する, ほとんどの公式を単純にコード化するのに十分なものを選びました. それらの公式は, ヨーロッパでのAレベル(訳注:イギリスの大学入学資格として認められる統一試験)または大学入試レベルに当たります.
The base set of content elements is chosen to be adequate for simple coding of most of the formulas used from kindergarten to the end of high school in the United States, and probably beyond through the first two years of college, that is up to A-Level or Baccalaureate level in Europe.
MathMLコンテント要素の集合の第一の役割は, 式の数学的構造を, それらを表現するのに使われる表記とは独立して, コード化することですが, 描画の課題は無視できません. コンテントMathMLの式を描画するには, MathML要素を直接実装することから, 表記の定義の宣言やXSLTスタイルシートに至るまでの, 様々な方法があります. コンテントMathMLの描画の必要事項は多岐に渡ることから, MathML3は, 描画のための標準の仕様を提供していません. その代わり, 典型的な描画を例示する方法で提案しています.
While the primary role of the MathML content element set is to directly encode the mathematical structure of expressions independent of the notation used to present the objects, rendering issues cannot be ignored. There are different approaches for rendering Content MathML formulae, ranging from native implementations of the MathML elements to declarative notation definitions, to XSLT style sheets. Because rendering requirements for Content MathML vary widely, MathML 3 does not provide a normative specification for rendering. Instead, typical renderings are suggested by way of examples.
4.1.3 厳格なコンテントMathML
Strict Content MathML
MathML3では, コンテントMathMLの部分集合もしくは概要である厳格なコンテントMathMLが定義されています. これは, 最小の, ただし十分な, 均一の構造で数学の意味を表現する要素の集合です. 完全なコンテントMathMLの文法は, MathML2との下位互換性のためであり, また, 冗長性と整然性の実用的なバランスを取ることに大まかに挑戦しています.
In MathML 3, a subset, or profile, of Content MathML is defined: Strict Content MathML. This uses a minimal, but sufficient, set of elements to represent the meaning of a mathematical expression in a uniform structure, while the full Content MathML grammar is backward compatible with MathML 2.0, and generally tries to strike a more pragmatic balance between verbosity and formality.
コンテントMathMLは, 巨大な数の空要素としてコード化される定義済の関数(例えば, sin, logなど)や複合したものを形作る様々な構造(例えば, set, intervalなど)を提供しています. 対照的に, 厳格なコンテントMathMLは, 全ての関数を表す外部のコンテント辞書の外部定義を指し示す属性と単独の要素(csymbol)を使用して, 複合したものを組み立てるのにapplyとbindのみを使用します. ciやcnといった素子要素も, 厳格なコンテントMathMLの一部と見なされますが, 属性の種類と文字列の内容がより制限されています.
Content MathML provides a large number of predefined functions
encoded as empty elements (e.g. sin, log, etc.)
and a variety of constructs for forming compound objects
(e.g. set, interval, etc.). By contrast, Strict
Content MathML uses a single element (csymbol) with an
attribute pointing to an external definition in extensible content
dictionaries to represent all functions, and uses only
apply and bind for building up compound
objects. The token elements such as ci and cn are
also considered part of Strict Content MathML, but with a more
restricted set of attributes and with content restricted to
text.
厳格なコンテントMathMLは, OpenMath(すなわち, [OpenMath2004]の見解によるOpenMathオブジェクトのXMLコード化)と互換性があるように設計されています. OpenMathは, 外部のコンテント辞書の利用を通して, 整然とした数学事象と意味を表現するための標準です. 下の表は, OpenMathオブジェクトのOpenMath XMLコード化と厳格なコンテントMathMLの要素の対応を示しています.
Strict Content MathML is designed to be compatible with OpenMath (in fact it is an XML encoding of OpenMath Objects in the sense of [OpenMath2004]). OpenMath is a standard for representing formal mathematical objects and semantics through the use of extensible Content Dictionaries. The table below gives an element-by-element correspondence between the OpenMath XML encoding of OpenMath objects and Strict Content MathML.
| 厳格なコンテントMathML Strict Content MathML |
OpenMath OpenMath |
|---|---|
cn |
OMI, OMF |
csymbol |
OMS |
ci |
OMV |
cs |
OMSTR |
apply |
OMA |
bind |
OMBIND |
bvar |
OMBVAR |
share |
OMR |
semantics |
OMATTR |
annotation,
annotation-xml |
OMATP, OMFOREIGN |
cerror |
OME |
cbytes |
OMB |
MathML3において, 公式な意味のコンテントMathMLの式は, 等しい厳格なコンテントMathMLの式を指定することで示されます. 厳格なコンテントMathMLの式は全て, OpenMathコンテント辞書によって与えられる注意深く定義された意味を持っていることから, 全てのコンテントMathMLの式は, この方法で明確に決められた意味を継承します. 対応を確実なものにするため, 厳格でないコンテントMathMLの構造を, 同じ意味の厳格なコンテントMathMLに書き換えるのに適用される変換の決まりについて, アルゴリズムが示されます. 個々の決まりは, この章の文章の中で紹介されています. 第4.6節 厳格なコンテントMathMLへの変換では, 全体としてのアルゴリズムについて述べています.
In MathML 3, formal semantics Content MathML expressions are given by specifying equivalent Strict Content MathML expressions. Since Strict Content MathML expressions all have carefully-defined semantics given in terms of OpenMath Content Dictionaries, all Content MathML expressions inherit well-defined semantics in this way. To make the correspondence exact, an algorithm is given in terms of transformation rules that are applied to rewrite non-Strict MathML constructs into a strict equivalents. The individual rules are introduced in context throughout the chapter. In Section 4.6 The Strict Content MathML Transformation, the algorithm as a whole is described.
ほとんどの変換の決まりは, 似た引数の構造を持つMathML要素の種類に関係しており, それらの種類を定義している第4.3.4節 演算子の種類で紹介しています. 特定の要素に対する特別な状況の決まりは, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで示しているものもあります. 第4.2節 式の構造をコード化するコンテントMathML要素での変換は, 核となるコンテントMathMLの厳格でない利用にとって重要です. 第4.3節 具体的な構造に対するコンテントMathMLでの変換には, 厳格なコンテントMathMLでは直接対応していない追加の構造の書き換えに重要なものもあります.
As most transformation rules relate to classes of MathML elements that have similar argument structure, they are introduced in Section 4.3.4 Operator Classes where these classes are defined. Some special case rules for specific elements are given in Section Section 4.4 Content MathML for Specific Operators and Constants. Transformations in Section 4.2 Content MathML Elements Encoding Expression Structure concern non-Strict usages of the core Content MathML elements, those in Section 4.3 Content MathML for Specific Structures concern the rewriting of some additional structures not directly supported in Strict Content MathML.
第4.6節 厳格なコンテントMathMLへの変換で説明する完全なアルゴリズムは, 全てのコンテントMathMLの式に厳格なコンテントMathMLによって特定の意味を与える上で完璧です. このことは, そのアルゴリズムが, 意味がMathML2で不十分に指定されていた式に, 特定の厳格な実装を与えなければならないことを意味しています. このアルゴリズムの意図は, 数学的直観に忠実であることです. ただし, アルゴリズムの標準の実装が, 直観より前に破綻するかもしれない余地は残るでしょう.
The full algorithm described inSection 4.6 The Strict Content MathML Transformation is complete in the sense that it gives every Content MathML expression a specific meaning in terms of a Strict Content MathML expression. This means it has to give specific strict interpretations to some expressions whose meaning was insufficiently specified in MathML2. The intention of this algorithm is to be faithful to mathematical intuitions. However edge cases may remain where the normative interpretation of the algorithm may break earlier intuitions.
適合したMathML処理ソフトウェアは, 変換を実装する必要はありません. それらの変換の決まりの存在は, ソフトウェアが等しい式を同一と扱わなければならないことを意味しません. 特に, ソフトウェアは, 変換の決まりが数学的に同一であると示されている式に対して, 異なった表現の描画をするかもしれません.
A conformant MathML processor need not implement this transformation. The existence of these transformation rules does not imply that a system must treat equivalent expressions identically. In particular systems may give different presentation renderings for expressions that the transformation rules imply are mathematically equivalent.
4.1.4 コンテント辞書
Content Dictionaries
数学の本質的特徴から, 数式の意味を形式化するどの方法も拡張可能でなければなりません. 拡張性の鍵は, 数学の論説の分野を広げるために, 新しい関数や他の記号を定義することが可能であることです. これを実現するには, 2つのことが必要です. コンテントMathMLによって既に定義されたものでない記号を表す仕組み, および, 特定の数学的意味と記号をあいまいでない手段で結び付ける方法が必要です. MathML3では, csymbol要素は, コンテント辞書が数学的意味を説明する手段である限り, 新しい記号を表す方法を提供します. その結び付けは, csymbol要素のコンテント辞書の定義を指し示す属性を介して成し遂げられます. それらの属性の構文と利用方法は第4.2.3節 コンテントマークアップの記号 <csymbol>で詳しく説明しています.
Due to the nature of mathematics, any method for formalizing
the meaning of the mathematical expressions must be
extensible. The key to extensibility is the ability to define
new functions and other symbols to expand the terrain of
mathematical discourse. To do this, two things are required: a
mechanism for representing symbols not already defined by
Content MathML, and a means of associating a specific
mathematical meaning with them in an unambiguous way. In MathML
3, the csymbol element provides the means to represent
new symbols, while Content Dictionaries are the way
in which mathematical semantics are described. The association
is accomplished via attributes of the csymbol element
that point at a definition in a CD. The syntax and usage of
these attributes are described in detail in Section 4.2.3 Content Symbols <csymbol>.
コンテント辞書は, 数学的概念の定義を構造化した文書であり, OpenMath標準[OpenMath2004]を参照して下さい. 部品化と再利用を最大限行うために, コンテント辞書は, 密接に関係する概念に対する定義の比較的小さな集合を典型的に含んでいます. OpenMath協会は, MathMLで定義済みの記号の実装を含んでいるMathMLコンテント辞書を含む, 公式のコンテント辞書の巨大な集合を管理しています. 個々に開発されたコンテント辞書を, 開示や利用を容易にしているOpenMath協会の辞書に登録するよう提案する流れがあります. MathML3は, ほとんどの場合に, 全ての利用者のソフトウェアで利用可能な公式のコンテント辞書を参照することによって, 意味のマークアップの目標を満たすことが最良であろうにも関わらず, コンテント辞書を公に利用できることを必要としてはいません.
Content Dictionaries are structured documents for the definition of mathematical concepts; see the OpenMath standard, [OpenMath2004]. To maximize modularity and reuse, a Content Dictionary typically contains a relatively small collection of definitions for closely related concepts. The OpenMath Society maintains a large set of public Content Dictionaries including the MathML CD group that including contains definitions for all pre-defined symbols in MathML. There is a process for contributing privately developed CDs to the OpenMath Society repository to facilitate discovery and reuse. MathML 3 does not require CDs be publicly available, though in most situations the goals of semantic markup will be best served by referencing public CDs available to all user agents.
後の文章のとおり, 定義済のMathML記号に対する意味の説明は, OpenMath協会がW3C数学作業部会と共同で開発したコンテント辞書を参照しています. ただし, この情報は有益ですが, 標準ではないことに注意することが重要です. 一般に定義済の記号の正確な数学的意味は, 完全にMathML3勧告で指定されている訳ではなく, 記号の意味についての標準の内容は, この章の文章に存在する内容のみです. OpenMath"コンテント"コンテント辞書により提供される意味の定義は, ほとんどのソフトウェアにとって十分なものを意図されており, MathML2.0勧告の類似した構造を特定している意味と一般に互換性があります. しかしながら, とても正確な意味が必要とされる状況(例えば, 数式処理システムの間の通信, 定理の証明といった整然としたシステムなど)で, OpenMathコンテント辞書により適切に提供された定義を, 確かめたり検証したり置き換えたりすることは, 実装を行う関係団体の責任です.
In the text below, descriptions of semantics for predefined MathML symbols refer to the Content Dictionaries developed by the OpenMath Society in conjunction with the W3C Math Working Group. It is important to note, however, that this information is informative, and not normative. In general, the precise mathematical semantics of predefined symbols are not not fully specified by the MathML 3 Recommendation, and the only normative statements about symbol semantics are those present in the text of this chapter. The semantic definitions provided by the OpenMath Content CDs are intended to be sufficient for most applications, and are generally compatible with the semantics specified for analogous constructs in the MathML 2.0 Recommendation. However, in contexts where highly precise semantics are required (e.g. communication between computer algebra systems, within formal systems such as theorem provers, etc.) it is the responsibility of the relevant community of practice to verify, extend or replace definitions provided by OpenMath CDs as appropriate.
4.1.5 コンテントMathMLの概念
Content MathML Concepts
コンテントMathMLの式の組み立ての基本となる種類は, 数字, 識別子, 記号です. これらの基本となる種類は, 関数の適用やまとめる演算子を利用して組合せられます. これらの鍵となる数学的概念の基本的な理解を持つことや, どのようにコンテントMathMLの設計に反映するかは重要です. 読者に便利なように, これらの概念をここで反復します.
The basic building blocks of Content MathML expressions are numbers, identifiers and symbols. These building blocks are combined using function applications and binding operators. It is important to have a basic understanding of these key mathematical concepts, and how they are reflected in the design of Content MathML. For the convenience of the reader, these concepts are reviewed here.
式"x+y"において, xは数学の変数で, 固定の値でない量を表す識別子を意味しています. このxは整数であるといった別の特性も持っているかもしれませんが, その値は固定された特性ではありません. 対照的に, プラス記号は, 固定された外部で定義されたもので, すなわち加算の関数を表します. このような識別子は, 変数と区別するために記号と呼ばれます. 一般的な初等関数と演算子は全て固定の外部の定義を持っており, それゆえに記号です。コンテントMathMLは, 変数を表すのにci要素を, 記号を表すのにcsymbol要素を使用します.
In the expression "x+y",
x is a mathematical variable, meaning an identifier that
represents a quantity with no fixed value. It may have other
properties, such as being an integer, but its value is not a fixed
property. By contrast, the plus sign is an identifier that represents a
fixed and externally defined object, namely the addition function.
Such an identifier is termed a symbol, to distinguish it
from a variable. Common elementary functions and operators all have
fixed, external definitions, and are hence symbols. Content MathML
uses the ci element to represent variables, and the
csymbol to represent symbols.
記号と変数を組合せる最も基本的な方法は, 関数の適用です. コンテントMathMLは, 関数自身(正弦関数といった記号やfといった変数)と, 引数に関数を適用した結果の間の, 決定的な意味の区別を行います. apply要素は, 関数と引数を構造上まとめ, 引数に関数を適用した場合に返される式を表します.
The most fundamental way in which symbols and variables are
combined is function application. Content MathML makes a crucial
semantic distinction between a function itself (a symbol such as the
sine function, or a variable such as f) and the result of
applying the function to arguments. The apply element groups the function
with its arguments syntactically, and represents the expression
resulting from applying that function to its arguments.
数学的に, 変数は, 束縛変数と自由変数に分けられます. 束縛変数は, ある適用範囲の中で束縛する演算子によって特別な役割を与えられた変数です. 例えば, 総和の中の添え字変数が束縛変数です. それらは, 式の根底の意味を変えることなく, 決められた範囲の中でいつも変化するという特性を持っている変数として, 特徴付けられます. 束縛されていない変数は, 自由変数と呼ばれています. 束縛変数と自由変数の間の論理的な区別は, 明確な意味で重要なことから, コンテントMathMLは, 例えばf(x)といった自由変数への関数の適用と, 適用範囲の中で束縛変数の演算を区別します. bind要素は, 束縛する範囲を表すのに利用され, 束縛する演算子と束縛変数を, bvar要素で示されているようにまとめます.
Mathematically, variables are divided into bound and
free variables. Bound variables are variables that are
assigned a special role by a binding operator within a certain scope.
For example, the index variable within a summation is a bound
variable. They can be characterized as variables with the property
that they can be renamed consistently throughout the binding scope
without changing the underlying meaning of the expression. Variables
that are not bound are termed free variables.
Because the logical distinction between bound and free variables is
important for well-defined semantics, Content MathML differentiates
between the application of a function to a free variable,
e.g. f(x) and the operation of binding a
variable within a scope. The bind element is used the delineate
the binding scope, and group the binding operator with its bound
variables, which are indicated by the bvar element.
厳格なコンテントマークアップにおいて, bind要素は, 変数を束縛した状態にする唯一の方法です. ただし, 厳格でない利用では, コンテントマークアップは, 総和や積分の"limit"といった, よく知られた慣用表現にとてもよく似たものを提供します. それらの構成は, 積分変数や総和の添え字変数といった具合に, よく暗に変数を束縛します. MathMLは, それらの構造で必要な極限といった補助データを表すのに利用される要素を, 修飾要素と呼びます.
In Strict Content markup, the bind element is the only way
of performing variable binding. In non-Strict usage, however, markup
is provided that more closely resembles well-known idiomatic
notations, such as the "limit" notations for sums and
integrals. These constructs often implicitly bind variables, such as
the variable of integration, or the index variable in a sum. MathML
terms the elements used to represent the auxiliary data such as limits
required by these constructions qualifier elements.
修飾要素を含む式は, それぞれが同じような束縛する演算子の種類に適用される, 少ない数の慣用的なパターンの1つに従います. 例えば, 総和と総積は, 同じパターンに従う添え字変数を使用することから同じ種類です. コンテントMathMLの演算子の種類は第4.3.4節 演算子の種類で詳しく説明されています.
Expressions involving qualifiers follow one of a small number of idiomatic patterns, each of which applies to class of similar binding operators. For example, sums and products are in the same class because they use index variables following the same pattern. The Content MathML operator classes are described in detail in Section 4.3.4 Operator Classes.
コンテントMathMLの各要素は, 要素について鍵となる情報を要約した表で始まる, 後の方の節で説明されます. 例えば, それらは, 異なる厳格な利用と厳格でない利用を持っており, それらの構文の表は明確に2つの状況を区分するために, 分割されています. 要素の内容としては, 付録A MathMLの処理のMathMLスキーマにリンクしている, 内容の例で示されます. 属性と属性値の行は同じようにスキーマをリンクしています. 適用可能な種類の行は, 演算子の種類を指定しており, どのくらいの数の引数がその要素を表現する演算子に必要かを示し, 多くの場合に第4.3.4節 演算子の種類で述べるように, 厳格なコンテントMathMLへの対応付けを決めています. 最後に, 修飾要素の行は, 演算子が修飾要素であるかどうか明確にしています. 種類と修飾要素は, applyの中の演算子要素にどれくらいの兄弟要素が続くのか, または入れ物となる要素の子要素を指定することに注意して下さい. 詳しくは, 第4.2.5節 関数の適用<apply>と第4.3.3節 修飾要素を参照して下さい.
Each Content MathML element is described in a section below that
begins with a table summarizing the key information about the element.
For elements that have different Strict and non-Strict
usage, these syntax tables are divided to clearly separate the two cases. The element's content
model is given in the Content row, linked to the MathML
Schema in Appendix A Parsing MathML. The Attributes, and
Attribute Values rows similarly link to the schema. Where
applicable, the Class row specifies the operator class, which
indicate how many arguments the operator represented by this element
takes, and also in many cases determines the mapping to Strict Content
MathML, as described in Section 4.3.4 Operator Classes. Finally,
the Qualifiers row clarifies whether the operator takes
qualifiers and if so, which. Note Class
and Qualifiers specify how many siblings may follow
the operator element in an apply, or the children of the
element for container elements; see Section 4.2.5 Function Application <apply> and Section 4.3.3 Qualifiers for
details).
4.2 式の構造をコード化するコンテントMathML要素
Content MathML Elements Encoding Expression Structure
この節では, コンテントMathMLの式の構造をコード化するための要素について紹介します. それらの要素は, 厳格なコンテントMathMLのコード化で使用される唯一のものです. 具体的に言うと次のものです.
In this section we will present the elements for encoding the structure of content MathML expressions. These elements are the only ones used for the Strict Content MathML encoding. Concretely, we have
-
基本の式, すなわち, 数字, 文字列, バイト列, 記号, 識別子.
basic expressions, i.e. Numbers, string literals, encoded bytes, Symbols, and Identifiers.
-
derived expressions, i.e. function applications and binding expressions, and
完全なコンテントMathMLは, さらに第4.3節 具体的な構造に対するコンテントMathMLと第4.4節 具体的な演算子と定数に対するコンテントMathMLで表された要素を含み, この節で表現するより豊かな内容モデルを持ちます. 厳格な利用と厳格でない利用は, それぞれの後で示す厳格な要素を論じる節で, 強調して表します.
Full Content MathML allows further elements presented in Section 4.3 Content MathML for Specific Structures and Section 4.4 Content MathML for Specific Operators and Constants, and allows a richer content model presented in this section. Differences in Strict and non-Strict usage of are highlighted in the sections discussing each of the Strict element below.
4.2.1 数字 <cn>
Numbers <cn>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|||
|---|---|---|---|---|
| 種類 Class |
Cn | Cn | ||
| 属性 Attributes |
CommonAtt, type | CommonAtt, DefEncAtt, type?, base? | ||
type属性の値type Attribute Values
|
"integer" | "real" | "double" | "hexdouble" |
"integer" |
"real" |
"double" |
"hexdouble" |
"e-notation" |
"rational" |
"complex-cartesian" |
"complex-polar" |
"constant" | 文字列 text |
既定値はreal ddefault is real |
|
base属性の値base Attribute Values
|
integer | 既定値は10 default is 10 |
||
| 内容 Content |
文字列 text |
(文字列 | mglyph | sep | PresentationExpression)* text |
||
cn要素は数字を表すのに使用されるコンテントMathML要素です. 厳格なコンテントMathMLは, 整数, 実数, 倍精度浮動小数点数に対応しています. 数字のこれらの型において, cnの中身は文字列です. 加えて, cnは, sep要素を利用して別々の部分に分けられた有理数や複素数に対応しています. sepを利用した構造は, 厳格なコンテントMathMLにおいては, 後で述べるapplyを使用した構造に書き換えられるでしょう.
The cn element is the Content MathML element used to
represent numbers. Strict Content MathML supports integers, real numbers,
and double precision floating point numbers. In these types of numbers,
the content of cn is text. Additionally, cn
supports rational numbers and complex numbers in which the different
parts are separated by use of the sep element. Constructs
using sep may be rewritten in Strict Content MathML as
constructs using apply as described below.
type属性は, cn要素の中でどの種類の数字が表されているか指定します. 既定値は"real"です. 各型は, 中身が後で述べるある形式であることを示します.
The type attribute specifies which kind of number is
represented in the cn element. The default value is
"real". Each type implies that the content be of
a certain form, as detailed below.
4.2.1.1 数字を表す<cn>,<sep/>の描画
Rendering <cn>,<sep/>-Represented Numbers
cnの中身の文字列の通常の描画は, プレゼンテーション要素mnのものと同じで, 下で一覧にするように, 使用されている属性, またはsepの状況に応じて提示される異なった形式があります.
The default rendering of the text content of cn is the same as that of the Presentation element mn, with suggested variants in the
case of attributes or sep being used, as listed below.
4.2.1.2 <cn>の厳格な利用
Strict uses of <cn>
厳格なコンテントMathMLでは, type属性は, 値"integer", "real", "hexdouble", "double"のみが使用されるでしょう.
In Strict Content MathML, the type attribute is mandatory, and may only take the values
"integer", "real", "hexdouble" or
"double":
- integer
- 整数は, 必須でない符号とそれに続く1つ以上の10進数の"数字"で表されます.
An integer is represented by an optional sign followed by a string of one or more decimal "digits". - real
- 実数は, 基数表記法で表されます. 基数表記法は, 必須ではない符号("+"または"-")と, それに続く小数点で整数部分と小数部分に分けられるであろう数字の文字列で構成されます. 例としては, 0.3, 1, -31.56があります.
A real number is presented in radix notation. Radix notation consists of an optional sign ("+" or "-") followed by a string of digits possibly separated into an integer and a fractional part by a decimal point. Some examples are 0.3, 1, and -31.56. - double
- この型は, IEEE754標準書式[IEEE754]で表現できる倍精度浮動小数点数を記述するのに使用されます. この型は, (数学の)実数の集合, 負のゼロ, 正負の無限, "非数"値の集合を含みます. IEEE倍精度浮動小数点数として
cnの文字列の中身を解釈するときの語彙の決まりは, XMLスキーマ第2部:データ型第2版[XMLSchemaDatatypes]の第3.1.2.5節に従います. 例えば, -1E4, 1267.43233E12, 12.78e-2, 12 , -0, 0, INF(無限)は, 全てこの書式で有効な倍精度浮動小数点数です.
This type is used to mark up those double-precision floating point numbers that can be represented in the IEEE 754 standard format [IEEE754]. This includes a subset of the (mathematical) real numbers, negative zero, positive and negative real infinity and a set of "not a number" values. The lexical rules for interpreting the text content of acnas an IEEE double are specified by Section 3.1.2.5 of XML Schema Part 2: Datatypes Second Edition [XMLSchemaDatatypes]. For example, -1E4, 1267.43233E12, 12.78e-2, 12 , -0, 0 and INF are all valid doubles in this format. - hexdouble
-
この型は, IEEE754倍精度浮動小数点数の64ビットを16進数として直接表現するのに使用します. よって, その数字は, 仮数, 指数, 符号を, 最下位ビットから順番に一番下から一番上のビットに向かって表します. この型は, 0-9, A-Fの16個の数字の文字列から構成されます. 次の例は, NaN(非数)値を表しています. 例のNaN(非数)といったIEEE倍精度浮動小数点数を, "double"型に対する語彙的な書式で表すことはできません.
This type is used to directly represent the 64 bits of an IEEE 754 double-precision floating point number as a 16 digit hexadecimal number. Thus the number represents mantissa, exponent, and sign from lowest to highest bits using a least significant byte ordering. This consists of a string of 16 digits 0-9, A-F. The following example represents a NaN value. Note that certain IEEE doubles, such as the NaN in the example, cannot be represented in the lexical format for the "double" type.
<cn type="hexdouble">7F800000</cn>
表示例
Sample Presentation
<mn>0x7F800000</mn>
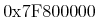
4.2.1.3 <cn>の厳格でない利用
Non-Strict uses of <cn>
base属性は, どのように中身が処理されるかを指定するのに利用されます. 属性値は, cnの中身が解釈される際の基数の値を示す10進数の正の整数です. base属性は, 要素の型が"integer"または"real"の場合のみ利用されるべきです. cn要素の他の型でのbase属性の利用は非推奨です. baseの既定値は"10"です.
The base attribute is used to specify how the content is
to be parsed. The attribute value is a base 10 positive integer
giving the value of base in which the text content of the cn
is to be interpreted. The base attribute should only be
used on elements with type "integer" or
"real". Its use on cn elements of other type
is deprecated. The default value for base is
"10".
type属性の追加の値は, e-notationsに対応するもの, 実数, 有理数, 複素数, 選ばれた重要な定数に対するものです. "integer", "real", "double", "hexdouble"型の場合, それらの各型は, 中身がどの形式かを示しています. type属性が省略された場合, 既定値は"real"です.
Additional values for the type attribute element for supporting
e-notations for real numbers, rational numbers, complex numbers and selected important
constants. As with the "integer", "real",
"double" and "hexdouble" types, each of these types
implies that the content be of a certain form. If the type attribute is
omitted, it defaults to "real".
- integer
-
整数は, 10でない基数に対応したものを表現できます.
baseが存在するなら, (10進数の)baseは, 数字をコード化する際の基数を指定します. よって,base='16'は, 16進数でのコード化を指定します.base> 10の場合, ラテン文字(A-Z, a-z)が, アルファベット順で数字として用いられます. 数字として用いられる文字の状態は記号ではありません. 次の例は, 10進数の32736をコード化したものです.Integers can be represented with respect to a base different from 10: If
baseis present, it specifies (in base 10) the base for the digit encoding. Thusbase='16' specifies a hexadecimal encoding. Whenbase> 10, Latin letters (A-Z, a-z) are used in alphabetical order as digits. The case of letters used as digits is not significant. The following example encodes the base 10 number 32736.<cn base="16">7FE0</cn>
表示例
Sample Presentation
<msub><mn>7FE0</mn><mn>16</mn></msub>
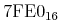
base> 36の場合, 整数の中には, 数字とアルファベットで表すことができないものもあります. 例えば, 次の例です.When
base> 36, some integers cannot be represented using numbers and letters alone. For example, while<cn base="1000">10F</cn>
これは, ほぼ問題なく, 10進数で1,000,015と書いた数字を表しています. 10進数で1,000,037と書く数字は,
baseが1000のとき, アルファベットと数字だけでは表せません. 結果として,base> 36のとき, (もしある場合に)数字として用いられる追加の文字の対応は, ソフトウェア次第です.arguably represents the number written in base 10 as 1,000,015, the number written in base 10 as 1,000,037 cannot be represented using letters and numbers alone when
baseis 1000. Consequently, support for additional characters (if any) that may be used for digits whenbase> 36 is application specific. - real
- 実数は, 10と異なる基数に関して表現することができます.
base属性が存在するなら, 1つ1つの数字は, ("integer"型で述べたものと同じ方法で)基数に応じて計算された数字として解釈されます.
Real numbers can be represented with respect to a base different than 10. If abaseattribute is present, then the digits are interpreted as being digits computed relative to that base (in the same way as described for type "integer"). - e-notation
-
実数は, この型を利用した特定の表記で表現されることもあるでしょう. そのような数字は,
<sep/>要素で区切られた2つの部分(仮数部と指数部)を持ちます. 1つ目の部分は実数で, 一方, 2つ目の部分は, 基数の累乗を示す整数の指数です.A real number may be presented in scientific notation using this type. Such numbers have two parts (a significand and an exponent) separated by a
<sep/>element. The first part is a real number, while the second part is an integer exponent indicating a power of the base.例えば,
<cn type="e-notation">12.3<sep/>5</cn>は, 12.3掛ける105を表します. この例の通常の表示は, 12.3e5です. この型はMathML2との下位互換性における使い勝手を第一としていますが, ほとんどの場合に, 数字がIEEE倍精度浮動小数点数の範囲ならば, "double"型を使用することが好まれることに注意して下さい.For example,
<cn type="e-notation">12.3<sep/>5</cn>represents 12.3 times 105. The default presentation of this example is 12.3e5. Note that this type is primarily useful for backwards compatibility with MathML 2, and in most cases, it is preferable to use the "double" type, if the number to be represented is in the range of IEEE doubles: - rational
-
有理数は, 比としての分子と分母として用いられる2つの整数として示されます. 分子と分母は
<sep/>で区切られます.A rational number is given as two integers to be used as the numerator and denominator of a quotient. The numerator and denominator are separated by
<sep/>.<cn type="rational">22<sep/>7</cn>
表示例
Sample Presentation
<mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow>
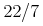
- complex-cartesian
-
直交座標系の複素数は, 実部と虚部を指定する2つの数字で示されます. 実部と虚部は
<sep/>要素で区切られ, それぞれの部分は前に述べた実数の形式を持ちます.A complex cartesian number is given as two numbers specifying the real and imaginary parts. The real and imaginary parts are separated by the
<sep/>element, and each part has the format of a real number as described above.<cn type="complex-cartesian"> 12.3 <sep/> 5 </cn>
表示例
Sample Presentation
<mrow> <mn>12.3</mn><mo>+</mo><mn>5</mn><mo>⁢<!--INVISIBLE TIMES--></mo><mi>i</mi> </mrow>
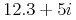
- complex-polar
-
極座標表示の複素数は, 絶対値と角度を指定する2つの数字で示されます. 絶対値と角度は
<sep/>で区切られ, それぞれの部分は前に述べた実数の形式を持ちます.A complex polar number is given as two numbers specifying the magnitude and angle. The magnitude and angle are separated by the
<sep/>element, and each part has the format of a real number as described above.<cn type="complex-polar"> 2 <sep/> 3.1415 </cn>
表示例
Sample Presentation
<mrow> <mn>2</mn> <mo>⁢<!--INVISIBLE TIMES--></mo> <msup> <mi>e</mi> <mrow><mi>i</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mn>3.1415</mn></mrow> </msup> </mrow>
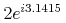
<mrow> <mi>Polar</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mn>2</mn><mn>3.1415</mn></mfenced> </mrow>
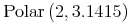
- constant
-
typeの値が"constant"の場合, 中身は, よく知られた定数のユニコード表現であるべきです. 重要な定数やそれらのユニコード表現については, いくつか後で一覧にしています.If the value
typeis "constant", then the content should be a Unicode representation of a well-known constant. Some important constants and their common Unicode representations are listed below.この
cnの型は, MathML1.0との下位互換性を主目的としています. MathML2.0は, 定数を表す<pi/>といった, たくさんの空要素を導入しました. そして, それらの表現や厳格なcsymbolの表現を使用する方が好まれます.This
cntype is primarily for backward compatibility with MathML 1.0. MathML 2.0 introduced many empty elements, such as<pi/>to represent constants, and using these representations or a Strict csymbol representation is preferred.
type属性の追加の値に加えて, cn要素の中身は, (厳格なコンテントMathMLで認められたsepに加えて)現在ユニコードで利用できない文字を参照するmglyph要素, または描画に利用される(第4.1.2節 コンテントMathMLの式の構造と範囲参照)一般的な構造のプレゼンテーションマークアップ(第3.1.9節 プレゼンテーション要素の概要参照)を含むことができます.
In addition to the additional values of the type attribute, the
content of cn element can contain (in addition to the
sep element allowed in Strict Content MathML) mglyph
elements to refer to characters not currently available in Unicode, or
a general presentation construct (see Section 3.1.9 Summary of Presentation Elements),
which is used for rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions).
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
base属性が存在するなら, base属性は, 両方の整数の数字のコード化に使われる基数を指定します. 有理数"rational"と一緒にbaseを使用することは非推奨です.
If a base attribute is present, it specifies the base used for the digit
encoding of both integers. The use of base with
"rational" numbers is deprecated.
書き換え: cn sep
Rewrite: cn sep
cnの子要素sepがあるとき, 現れた文字列はcn要素として書き換えられるでしょう. sepを含むcn要素がbase属性も持っている場合, base属性は, 下で示すように, 書き換え後の記号の各引数cnに複写されます.
If there are sep children of the cn,
then intervening text may be rewritten as cn
elements. If the cn element containing sep
also has a base attribute, this is copied to each
of the cn arguments of the resulting symbol, as
shown below.
<cn type="" base=""><sep/></cn>
この式は次のように書き換えられます.
is rewritten to
<apply><csymbol cd=""></csymbol> <cn type="integer" base=""></cn> <cn type="integer" base=""></cn> </apply>
書き換え後に使用される記号は, type属性に応じて次の表のようになります.
The symbol used in the result depends on the type attribute according to the following table:
| type属性 type attribute |
OpenMath記号 OpenMath Symbol |
|---|---|
| e-notation | bigfloat |
| rational | rational |
| complex-cartesian | complex_cartesian |
| complex-polar | complex_polar |
注意: bigfloatの場合, 記号は3つの引数を持ち, <cn type="integer">10</cn>が, 使われている指数の底を示すのに, 2番目の引数として挿入されるべきです.
Note: In the case of bigfloat the symbol
takes three arguments, <cn type="integer">10</cn> should be inserted as the second argument, denoting the base of the exponent used.
type属性が別の値を持つか, 複数の<sep/>要素がある場合, 現れた式は上のように変換されますが, 関数の適用における最初の引数に対する, ソフトウェア固有の記号の選択がされなければなりません.
If the type attribute has a different value,
or if there is more than one <sep/> element,
then the intervening expressions are converted as above,
but a system-dependent choice of symbol for the head of the application must be used.
base属性が使われている場合, 書き換えられた式は, 厳格なコンテントMathMLではなく, 各引数は再帰的に処理される必要があります.
If a base attribute has been used then the resulting expression is not Strict Content MathML, and each of the arguments needs to be recursively processed.
書き換え: cn based_integer
Rewrite: cn based_integer
10以外のbase属性の付いたcn要素は, 次のように書き換えられます.
A cn element with a base attribute other than 10 is rewritten as follows. (A base attribute with value 10 is simply removed) .
<cn type="" base=""></cn>
<apply><csymbol cd="nums1"></csymbol> <cn type="integer"></cn> <cs></cs> </apply>
元々の要素がtype属性に"integer"を指定していたり, type属性が無いが, 要素の内容が単に文字[a-zA-Z0-9]と空白で構成されていたりする場合, 書き換えられた関数の適用の先頭で使われる記号は, 示したようにbased_integerであるべきです. そうでない場合, based_floatが使われるべきです.
If the original element specified type "integer" or if there is no type attribute, but the content of the element just consists of the characters [a-zA-Z0-9] and white space then the symbol used as the head in the resulting application should be based_integer as shown. Otherwise it should be should be based_float.
書き換え: cn constant
Rewrite: cn constant
厳格なコンテントMathMLでは, 定数はcsymbol要素を使用して表現すべきです. 数々の重要な定数がnums1コンテント辞書で定義されています. 書き方の例は次のとおりです.
In Strict Content MathML, constants should be represented using
csymbol elements. A number of important constants are defined in the
nums1 content dictionary. An expression of the form
<cn type="constant"></cn>これと等価の厳格なコンテントMathMLは次のとおりです.
has the Strict Content MathML equivalent
<csymbol cd="nums1"></csymbol>cに対応するc2は, 次の表で指定されているとおりです.
where c2 corresponds to c as specified in the following table.
| 内容 Content |
説明 Description |
OpenMath記号 OpenMath Symbol |
|---|---|---|
U+03C0 (π)
|
三角法の通常のπ. およそ3.141592653... The usual π of trigonometry: approximately 3.141592653... |
pi |
U+2147 (ⅇ or ⅇ)
|
自然対数の底. およそ2.718281828... The base for natural logarithms: approximately 2.718281828... |
e |
U+2148 (ⅈ or ⅈ)
|
-1の平方根 Square root of -1 |
i |
U+03B3 (γ)
|
オイラーの定数. およそ0.5772156649... Euler's constant: approximately 0.5772156649... |
gamma |
U+221E (∞ or &infty;)
|
無限. 適切な解釈は文脈によって変わる Infinity. Proper interpretation varies with context |
infinity |
書き換え: cn プレゼンテーションMathML
Rewrite: cn presentation mathml
cnがプレゼンテーションMathMLのマークアップを含んでいる場合, 構築要素の引数が提供されたプレゼンテーションMathMLを付加したci要素になるという, 上の決まりの変形した形式を用いて, 厳格なコンテントMathMLに書き換えられます.
If the cn contains Presentation MathML markup, then it may
be rewritten to Strict MathML using variants of the rules above where
the arguments of the constructor are ci elements annotated
with the supplied Presentation MathML.
文字列でない内容の次の形式のcnの式があるとします.
A cn expression with non-text content of the form
<cn type=""> <sep/> </cn>
この式は, 次のように書き換えることで厳格なコンテントMathMLに変換されます.
is transformed to Strict Content MathML by rewriting it to
<apply><csymbol cd=""></csymbol> <semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics> <semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics> </apply>
識別子が名付けられる場合, (文字列でなければならない)pとqは, プレゼンテーションMathMLの内容から, ソフトウェアが定義した方法で, ひょっとしたら上の例のように要素のマークアップを無視した要素の文字データを使用して, 決められるべきでしょう. そのような書き換えを行うソフトウェアは, 同じプレゼンテーションMathMLの内容を使用した構造が同じciを用いたsemantics要素に書き換えられることを確実にすべきです. 逆に言えば, (プレゼンテーション要素が同じ文字データを持っていたとしても)異なるMathMLを使用した構造は, 違う識別子に書き換えられるべきです.
Where the identifier names, p and q, (which have to be a text string) should be
determined from the presentation MathML content, in a system defined way, perhaps as
in the above example by taking the character data of the element ignoring any element
markup. Systems doing such rewriting should ensure that constructs using the same
Presentation MathML content are rewritten to semantics elements using the
same ci, and that conversely constructs that use different MathML should be
rewritten to different identifier names (even if the Presentation MathML has the same character data).
関連する特別な例として, cn要素が厳格なコンテントMathMLの利用で認められていない文字データ, 例えば数字やアルファベットでない文字を含んでいる場合が挙げられます. 概念上, このことは, プレゼンテーションマークアップのmtext要素を含むcn要素に類似しており, そのため書き換えることができます. しかしながら, 書き換えられた付加情報は, 追加の描画情報を含まないであろうことから, そのようなデータは, semantics構造としてよりも, 直接ci要素として書き換えられるべきです.
A related special case arises when a cn element
contains character data not permitted in Strict Content MathML
usage, e.g. non-digit, alphabetic characters. Conceptually, this is
analogous to a cn element containing a presentation
markup mtext element, and could be rewritten accordingly.
However, since the resulting annotation would contain no additional
rendering information, such instances should be rewritten directly
as ci elements, rather than as a semantics
construct.
4.2.2 コンテントマークアップの識別子 <ci>
Content Identifiers <ci>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Ci | Ci |
| 属性 Attributes |
CommonAtt, type? | CommonAtt, DefEncAtt, type? |
type属性の値type Attribute Values
|
"integer"| "rational"| "real"| "complex"| "complex-polar"| "complex-cartesian"| "constant"| "function"| "vector"| "list"| "set"| "matrix" | 文字列 string |
| 修飾要素 Qualifiers |
BvarQ, DomainQ, degree, momentabout, logbase | |
| 内容 Content |
文字列 text |
文字列 | mglyph | PresentationExpression text |
コンテントMathMLは, ("コンテントマークアップの識別子"の覚えやすい略称である)ci要素を, 変数を構築するのに使用します. コンテントマークアップの識別子は, 特性を持つが値は持たない"数学変数"を表します. 例えば, xやyは, 式"x+y"の中の変数で, 変数xは次のように表されるでしょう.
Content MathML uses the ci element (mnemonic for "content
identifier") to construct a variable. Content identifiers
represent "mathematical variables" which have
properties, but no fixed value. For example, x and y are variables
in the expression "x+y", and the variable
x would be represented as
<ci>x</ci>
MathMLでは, 変数は, 固定の外部の定義を持ち, csymbol要素で表される記号とは区別されています.
In MathML, variables are distinguished from symbols, which have fixed, external definitions, and are represented by the csymbol element.
空白の(正規化)処理の後, ci要素の中身は, それ自身を識別する名前として解釈されます. 2つの変数の名前が同一のもので, 同じ適用範囲(議論については第4.2.6節 束縛と束縛変数 <bind>と<bvar>参照)にある場合, それらの変数が等しいと見なされます.
After white space normalization the content of a ci element is interpreted as a
name that identifies it. Two variables are considered equal, if and only if their names
are identical and in the same scope (see Section 4.2.6 Bindings and Bound Variables <bind>
and <bvar> for a
discussion).
4.2.2.1 <ci>の厳格な利用
Strict uses of <ci>
ci要素は, 自身が表現する数学的事象の基本の型を指定するために, type属性を使用します. 厳格なコンテントMathMLでは, 利用できる値の集合は, "integer", "rational", "real", "complex", "complex-polar", "complex-cartesian", "constant", "function", vector, list, set, matrixです. それらの値は, mathmltypesコンテント辞書の記号integer_type, rational_type, real_type, complex_polar_type, complex_cartesian_type, constant_type, fn_type, vector_type, list_type, set_type, matrix_typeに対応しています. この点で, 次の2つの式は等しいと見なされます.
The ci element uses the type attribute to specify the basic type of
object that it represents. In Strict Content MathML, the set of permissible values is
"integer", "rational", "real",
"complex", "complex-polar",
"complex-cartesian", "constant", "function",
vector, list, set, and matrix. These values correspond
to the symbols
integer_type,
rational_type,
real_type,
complex_polar_type,
complex_cartesian_type,
constant_type,
fn_type,
vector_type,
list_type,
set_type, and
matrix_type in the
mathmltypes Content Dictionary: In this sense the following two expressions are considered equivalent:
<ci type="integer">n</ci>
<semantics>
<ci>n</ci>
<annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content">
<csymbol cd="mathmltypes">integer_type</csymbol>
</annotation-xml>
</semantics>"complex"は"complex-cartesian"の別名と見なされるべきで, 同じcomplex_cartesian_type記号に書き換えられることに注意して下さい. 直交座標系の形式と極座標系の形式の区別は, 実際のところcnでのコード化された文字列の解釈にのみ影響するので, "complex"は, ひょっとしたらciで利用される自然な型かもしれません.
Note that "complex" should be considered
an alias for "complex-cartesian" and rewritten to the
same complex_cartesian_type
symbol. It is perhaps a more natural type name for use with
ci as the distinction between cartesian and polar form really
only affects the interpretation of literals encoded with cn.
4.2.2.2 <ci>の厳格でない利用
Non-Strict uses of <ci>
ci要素は, type属性にどんな文字列の値でも利用できます. 特に, 何らかのMathML入れ物要素の名前やそれらの型の値を利用できます.
The ci element allows any string value for the type
attribute, in particular any of the names of the MathML container elements or their type
values.
型のより発達した取扱いとしては, type属性は不適当です. 発達した型は, それ自身固有の有意義な構造(例えば, vector(complex))を必要とし, 数学的事象としておそらく最も良く構築されており, そのため, semantics要素の利用を通してMathMLの式と結び付けられます. より多くの例については, [MathML型情報]を参照して下さい.
For a more advanced treatment of types, the type attribute is
inappropriate. Advanced types require significant structure of their own (for example,
vector(complex)) and are probably best constructed as mathematical objects and
then associated with a MathML expression through use of the semantics
element. See [MathMLTypes] for more examples.
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
書き換え: ci type付加情報
Rewrite: ci type annotation
厳格なコンテントマークアップでは, type属性は, 意味付加情報を通して表現されます. 次の形式の式があるとします.
In Strict Content, type attributes are represented via semantic attribution. An expression of the form
<ci type=""></ci>
この式は次のように書き換えられます.
is rewritten to
<semantics> <ci></ci> <annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content"> <ci></ci> </annotation-xml> </semantics>
ci要素は, 現在ユニコードで利用できない文字を参照するmglyph要素, または描画に利用される(第4.1.2節 コンテントMathMLの式の構造と範囲参照)一般的な構造のプレゼンテーションマークアップ(第3.1.9節 プレゼンテーション要素の概要参照)を含むことができます.
The ci element can contain
mglyph elements to refer to characters not currently available in Unicode, or a
general presentation construct (see Section 3.1.9 Summary of Presentation Elements), which is used for
rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions).
書き換え: ci プレゼンテーションMathML
Rewrite: ci presentation mathml
文字列でない内容の次の形式のciの式があるとします.
A ci expression with non-text content of the form
<ci> </ci>この式は, 次のように書き換えることで厳格なコンテントMathMLに変換されます.
is transformed to Strict Content MathML by rewriting it to
<semantics> <ci></ci> <annotation-xml encoding="MathML-Presentation"> </annotation-xml> </semantics>
識別子が名付けられる場合, (文字列でなければならない)pとqは, プレゼンテーションMathMLの内容から, ソフトウェアが定義した方法で, ひょっとしたら上の例のように要素のマークアップを無視した要素の文字データを使用して, 決められるべきでしょう. そのような書き換えを行うソフトウェアは, 同じプレゼンテーションMathMLの内容を使用した構造が同じciを用いたsemantics要素に書き換えられることを確実にすべきです. 逆に言えば, (プレゼンテーション要素が同じ文字データを持っていたとしても)異なるMathMLを使用した構造は, 違う識別子に書き換えられるべきです.
Where the identifier name, p, (which has to be a text string) should be
determined from the presentation MathML content, in a system defined way, perhaps as
in the above example by taking the character data of the element ignoring any element
markup. Systems doing such rewriting should ensure that constructs using the same
Presentation MathML content are rewritten to semantics elements using the
same ci, and that conversely constructs that use different MathML should be
rewritten to different identifier names (even if the Presentation MathML has the same character data).
次の例は, 視覚的にC2を表示させる微小な記号をコード化したもので, 内容の目的に応じて単独の記号として扱われます.
The following example encodes an atomic symbol that displays visually as C2 and that, for purposes of content, is treated as a single symbol
<ci> <msup><mi>C</mi><mn>2</mn></msup> </ci>
これと等価な厳格なコンテントMathMLは次のとおりです.
The Strict Content MathML equivalent is
<semantics>
<ci>C2</ci>
<annotation-xml encoding="MathML-Presentation">
<msup><mi>C</mi><mn>2</mn></msup>
</annotation-xml>
</semantics>表示例
Sample Presentation
<msup><mi>C</mi><mn>2</mn></msup>
4.2.2.3 コンテント要素の識別子の描画
Rendering Content Identifiers
ci要素の中身がプレゼンテーションMathMLで構成されている場合, そのプレゼンテーションMathMLが使用されます. そのようなタグ付けがされていない場合, 中身の文字列が, mi要素の中身であるかのように表現されます. ソフトウェアが双方向の文字列の描画に対応している場合, 描画は, ユニコードの双方向の描画に従います.
If the content of a ci element consists of Presentation MathML, that
presentation is used. If no such tagging is supplied then the text
content is rendered as if it were the content of an mi element. If an
application supports bidirectional text rendering, then the rendering follows the
Unicode bidirectional rendering.
type属性は, 描画の情報を提供すると解釈されます. 例えば, 次の例があるとします.
The type attribute can be interpreted to
provide rendering information. For example in
<ci type="vector">V</ci>
描画ソフトウェアは, ベクトルとして太字のVを表示するでしょう.
a renderer could display a bold V for the vector.
4.2.3 コンテントマークアップの記号 <csymbol>
Content Symbols <csymbol>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Csymbol | Csymbol |
| 属性 Attributes |
CommonAtt, cd | CommonAtt, DefEncAtt, type?, cd? |
| 内容 Content |
SymbolName | 文字列 | mglyph | PresentationExpression text |
| 修飾要素 Qualifiers |
BvarQ, DomainQ, degree, momentabout, logbase |
csymbolは, 特定の, 数学的に定義された概念を外部定義と一緒に参照するのに使用されます. 式"x+y"では, プラス記号は, 特定の, 外部定義を持つ記号, つまり加算の関数です. MathML3は, そのような識別子を記号と呼びます. 初等関数と一般的な数学の演算子は全て, 記号の例です. "記号"という用語は, ここでは抽象的な意味で用いられ, 画面や紙に構築される, どの特定の表現とも関係がないことに注意して下さい.
A csymbol is used to refer to a specific,
mathematically-defined concept with an external definition. In the
expression "x+y", the plus sign is
a symbol since it has a specific, external definition, namely the addition function.
MathML 3 calls such an identifier a
symbol. Elementary functions and common mathematical
operators are all examples of symbols. Note that the term
"symbol" is used here in an abstract sense and has no
connection with any particular presentation of the construct on screen
or paper.
4.2.3.1 <csymbol>の厳格な利用
Strict uses of <csymbol>
csymbolは, 属性を通して特定の数学的概念の定義を参照することで表される, 自身の概念を指定します. 概念上, 外部定義への参照は単にURI, すなわち, 定義を唯一のものとして指定する名前です. ただし, 利用者のソフトウェア間の通信に使い勝手が良いように, 外部定義は共有されなければなりません.
The csymbol identifies the specific mathematical concept
it represents by referencing its definition via attributes.
Conceptually, a reference to an external definition is merely a URI,
i.e. a label uniquely identifying the definition. However, to be
useful for communication between user agents, external definitions
must be shared.
この理由から, 様々な長年続いている努力は, 定型的な, 数学的定義の公式な保管場所を開発するために続けられてきました. それらの中で最も注目すべきことは, コンテント辞書(CDs)のOpenMath協会の保管場所が, 規模が大きく, 開かれていて活動的なことです. MathML3では, OpenMath CDsは, 外部定義の好ましい情報源です. 特に, 既に定義されたMathML3の演算子と関数の定義は, OpenMath CDsによって示されています.
For this reason, several longstanding efforts have been organized to develop systematic, public repositories of mathematical definitions. Most notable of these, the OpenMath Society repository of Content Dictionaries (CDs) is extensive, open and active. In MathML 3, OpenMath CDs are the preferred source of external definitions. In particular, the definitions of pre-defined MathML 3 operators and functions are given in terms of OpenMath CDs.
MathML3は, 外部定義またはコンテント辞書を参照する2つの仕組みを提供しています. 1つ目は, cd属性を利用するもので, OpenMathにより確立された, 特にCDsを参照する慣習に従います. 2つ目は, definitionURL属性を利用するもので, MathML2との下位互換性のためのもので, URIで指定されるであろうCDsまたは何らかの他の定義の情報を参照するのに利用できます. このことについては, 次の節で説明します.
MathML 3 provides two mechanisms for referencing external definitions or content
dictionaries. The first, using the cd attribute, follows conventions
established by OpenMath specifically for referencing CDs. This is the
form required in Strict Content MathML. The second, using the
definitionURL attribute, is backward compatible with MathML 2, and can be used
to reference CDs or any other source of definitions that can be
identified by a URI. It is described in the following section
OpenMath CDsを参照するとき, 好ましい方法は, 次のようにcd属性を利用することです. 概念上は, OpenMathの記号の定義は, 同じ名前のCDsのあいまいさを無くすURIである3つの値, 記号の名前, CDの名前, 基となるCDによって指定されます. その3つの値とcsymbolを結び付けるため, csymbolの中身は記号の名前を指定し, コンテント辞書の名前はcd属性を用いて示されます. 基となるCDは, csymbolを含むmath要素を埋め込んでいる文書から, その文書によって示される仕組み, ソフトウェアの既定値, 囲っているmath要素によって指定されている場合もあるcdgroup属性のいずれかによって決められます. 第2.2.1節 属性を参照して下さい. 指定されている情報が無い場合, http://www.openmath.org/cdが, 全てのcsymbol要素, annotation, annotation-xmlに対する基となるCDと見なされます. これは, OpenMath協会によって参照されている標準のCDsの集合に対する基となるCDです.
When referencing OpenMath CDs, the preferred method is to use the cd
attribute as follows. Abstractly, OpenMath symbol definitions are identified by a triple
of values: a symbol name, a CD name, and a CD base,
which is a URI that disambiguates CDs of the same name. To associate such a triple with a
csymbol, the content of the csymbol specifies the symbol name, and the
name of the Content Dictionary is given using the cd attribute. The CD base is
determined either from the document embedding the math element which contains the
csymbol by a mechanism given by the embedding document format, or by system
defaults, or by the cdgroup attribute , which is optionally specified on the
enclosing math element; see Section 2.2.1 Attributes. In the absence
of specific information http://www.openmath.org/cd is assumed as the CD base
for all csymbol elements annotation, and annotation-xml. This
is the CD base for the collection of standard CDs maintained by the OpenMath Society.
cdgroupは, OpenMath CDグループファイルのURLを指定します. CDグループファイルの書式の詳細な説明については, [OpenMath2004]の第4.4.2節(CDグループ)を参照して下さい. 概念上, CDグループファイルは, CDの名前と対応する基となるCDの組の一覧です. csymbolがcd属性を用いてCDの名前を参照しているとき, その名前はCDグループファイルの中を検索され, 結び付けられた基となるCDの値がそのcsymbolに使用されます. CDグループファイルが指定されているが, 参照しているCDの名前がグループファイルの中で見つからない場合, またはグループファイルを検索する際にエラーが生じた場合, 参照しているcsymbolは定義されません. しかしながら, エラーが生じた場合の取り扱いは定義されておらず, 利用者のソフトウェアの責務です.
The cdgroup specifies a URL to an OpenMath CD Group file. For a detailed
description of the format of a CD Group file, see Section 4.4.2 (CDGroups)
in [OpenMath2004]. Conceptually, a CD group file is a list of
pairs consisting of a CD name, and a corresponding CD base. When a csymbol
references a CD name using the cd attribute, the name is looked up in the CD
Group file, and the associated CD base value is used for that csymbol. When a CD
Group file is specified, but a referenced CD name does not appear in the group file, or
there is an error in retrieving the group file, the referencing csymbol is not
defined. However, the handling of the resulting error is not defined, and is the
responsibility of the user agent.
外部定義への参照はURIであるにも関わらず, CDファイルは, URIをURLとして解釈して得られた場所で検索可能であることが強く推奨されます. 特に, 記号の定義された他の特性は, 指定されたコンテント辞書を詳しく調べることで利用できるでしょう. それらは, 記号の定義のみを含むのではなく, 例や他の公式な特性も含んでいます. ただし, OpenMathコンテント辞書には複数のコード化手法があり, CDを検索するときのコードを正確に決めるのは, 利用者のソフトウェア次第です.
While references to external definitions are URIs, it is strongly recommended that CD files be retrievable at the location obtained by interpreting the URI as a URL. In particular, other properties of the symbol being defined may be available by inspecting the Content Dictionary specified. These include not only the symbol definition, but also examples and other formal properties. Note, however, that there are multiple encodings for OpenMath Content Dictionaries, and it is up to the user agent to correctly determine the encoding when retrieving a CD.
4.2.3.2 <csymbol>の厳格でない利用
Non-Strict uses of <csymbol>
上で説明した形式に加えて, csymbol要素は, 現在ユニコードで利用できない文字を参照するmglyph要素, または描画に利用される(第4.1.2節 コンテントMathMLの式の構造と範囲参照)一般的な構造のプレゼンテーションマークアップ(第3.1.9節 プレゼンテーション要素の概要参照)を含むことができます. この場合に, 厳格なコンテントMathMLを書くときは, csymbolはci要素として扱われるべきで, 書き換え: ci プレゼンテーションMathMLを用いて書き換えられるべきです.
In addition to the forms described above, the csymbol and element can contain
mglyph elements to refer to characters not currently available in Unicode, or a
general presentation construct (see Section 3.1.9 Summary of Presentation Elements), which is used for
rendering (see Section 4.1.2 The Structure and Scope of Content MathML Expressions). In this case, when
writing to Strict Content MathML, the csymbol should be treated as a
ci element, and rewritten using Rewrite: ci presentation mathml.
(OpenMath CDsまたは他の)外部定義は, definitionURL属性を用いて直接csymbolに対して指定されることもあるでしょう. OpenMath記号の定義を参照するのに用いられるときは, (記号の名前, CDの名前, 基となるCDの)3つの概念が, 次のように完全な形のURIに対応付けられるでしょう.
External definitions (in OpenMath CDs or elsewhere) may also be specified directly for
a csymbol using the definitionURL attribute. When used to reference
OpenMath symbol definitions, the abstract triple of (symbol name, CD name, CD base) is
mapped to a fully-qualified URI as follows:
URI =基となるCD+ '/' +CDの名前+ '#' +記号の名前URI =cdbase+ '/' +cd-name+ '#' +symbol-name
例えば, 次の3つの概念があるとします.
For example,
(plus, arith1, http://www.openmath.org/cd)
これらは次のように対応付けられます.
is mapped to
http://www.openmath.org/cd/arith1#plus結果として生じるURIが, definitionURL属性の値として指定されます.
The resulting URI is specified as the value of the definitionURL attribute.
参照の形は, MathML2との下位互換性のために使い勝手が良く, (セマンティックウェブのRDF[rdf]またはOMDoc [OMDoc1.2]といった)URIに基づいた枠組みのなかでのコンテントMathMLの利用を容易にします. 他の恩恵としては, CDの記号の名前がcsymbol要素の中身と一致する必要がないことです. ただし, 一般にこの方法は, とても長いMathMLデータになります. また, CDsが開発中の状況では, CDグループファイルの利用は, マークアップを変えることなく, CDsの場所の変更を可能にします。definitionURLの3つめの不利な点としては. cd属性とは違い, OpenMathコンテント辞書の記号の定義を参照しているとは限らないことです. よって, 一般に, 利用者のプログラムが, 文脈や, MathMLデータが現れた場所の共通の慣習についての詳細な情報無しに, definitionURLの値の適切な解釈を自分で決めることは困難です.
This form of reference is useful for backwards compatibility with MathML2 and to
facilitate the use of Content MathML within URI-based frameworks (such as RDF [rdf] in the Semantic Web or OMDoc [OMDoc1.2]). Another benefit is
that the symbol name in the CD does not need to correspond to the content of the
csymbol element. However, in general, this method results in much longer MathML
instances. Also, in situations where CDs are under development, the use of a CD Group
file allows the locations of CDs to change without a change to the markup. A third
drawback to definitionURL is that unlike the cd attribute, it is not
limited to referencing symbol definitions in OpenMath content dictionaries. Hence, it is
not in general possible for a user agent to automatically determine the proper
interpretation for definitionURL values without further information about the
context and community of practice in which the MathML instance occurs.
外部参照のcdとdefinitionURL両方の仕組みが, 単独のMathMLデータの中で使われているかもしれません. ただし, cdとdefinitionURL属性の両方が, 単独のcsymbolで指定されている場合, cd属性が優先されます.
Both the cd and definitionURL mechanisms of external reference
may be used within a single MathML instance. However, when both a cd and a
definitionURL attribute are specified on a single csymbol, the
cd attribute takes precedence.
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
厳格でない利用では, csymbolはtype属性を利用できます.
In non-Strict usage csymbol allows the use of
a type attribute.
書き換え: csymbol type付加情報
Rewrite: csymbol type annotation
厳格なコンテントMathMLでは, type属性は, 意味付加情報を通して表現されます. 次の形式の式があるとします.
In Strict Content, type attributes are represented via semantic attribution. An expression of the form
<csymbol type="">symbolname</csymbol>この式は次のように書き換えられます.
is rewritten to
<semantics>
<csymbol>symbolname</csymbol>
<annotation-xml cd="mathmltypes" name="type" encoding="MathML-Content">
<ci></ci>
</annotation-xml>
</semantics>4.2.3.3 記号の描画
Rendering Symbols
csymbol要素の中身がプレゼンテーションMathMLで構成されている場合, そのプレゼンテーションMathMLが使用されています. そのようなタグ付けがされていない場合, 中身の文字列が, mi要素の中身であるかのように表現されます. ソフトウェアが双方向の文字列の描画に対応している場合, 描画は, ユニコードの双方向の描画に従います.
If the content of a csymbol element is tagged using presentation tags,
that presentation is used. If no such tagging is supplied then the text
content is rendered as if it were the content of an mi element. In
particular if an application supports bidirectional text rendering, then the
rendering follows the Unicode bidirectional rendering.
4.2.4 文字列<cs>
String Literals <cs>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Cs | Cs |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
文字列 text |
文字列 text |
cs要素は, コンテントMathMLの式で用いられるであろう"文字列"をコード化します.
The cs element encodes "string literals"
which may be used in Content MathML expressions.
csの中身は文字列です. プレゼンテーションMathMLの構成は, 厳格でないマークアップであっても何ら認められていません. とりわけ, csはmglyph要素を含まないでしょうし, その中身は空白の(正規化)処理を受けません.
The content of cs is text; no
Presentation MathML constructs are allowed even when used in
non-strict markup. Specifically, cs may not contain
mglyph elements, and the content does not undergo white space
normalization.
コンテントMathML
Content MathML
<set> <cs>A</cs><cs>B</cs><cs> </cs> </set>
表示例
Sample Presentation
<mrow>
<mo>{</mo>
<ms>A</ms>
<mo>,</mo>
<ms>B</ms>
<mo>,</mo>
<ms> <!--NO-BREAK SPACE--> <!--NO-BREAK SPACE--></ms>
<mo>}</mo>
</mrow>4.2.5 関数の適用 <apply>
Function Application <apply>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Apply | Apply |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
ContExp+ | ContExp+ | (ContExp, BvarQ, Qualifier?, ContExp*) |
数学の複雑な事象を組み立てる最も基本的な方法は, 関数や演算子を引数に適用することです.
The most fundamental way of building a compound object in mathematics is by applying a function or an operator to some arguments.
4.2.5.1 厳格なコンテントMathML
Strict Content MathML
MathMLでは, apply要素が, その引数に関数や演算子を適用することを表す式のツリー構造を組み立てるのに利用されます. 生じたツリー構造は, 完全な数式に対応します. ざっくり言うと, このツリー構造は, かっこや意味を変えることのない"論理的なかっこ"で囲まれた数学の一部分を意味します.
In MathML, the apply element is used to build an expression tree that
represents the application a function or operator to its arguments. The
resulting tree corresponds to a complete mathematical expression. Roughly
speaking, this means a piece of mathematics that could be surrounded by
parentheses or "logical brackets" without changing its meaning.
例えば, (x + y)は次のようにコード化されるでしょう.
For example, (x + y) might be encoded as
<apply><csymbol cd="arith1">plus</csymbol><ci>x</ci><ci>y</ci></apply>
applyの開始タグと終了タグは, 何らかの演算子や関数の適用範囲を正確に指定します. 最も典型的なapplyの使い方は単純で再帰的です. 記号で, 内容モデルは次のように説明できます.
The opening and closing tags of apply specify exactly the scope of any
operator or function. The most typical way of using apply is simple and
recursive. Symbolically, the content model can be described as:
<apply> op [ a b ...] </apply>
被演算子 a, b, ... は, MathMLの式のツリー構造自身であり, opは, 演算子や関数を表すMathMLの式のツリー構造です. applyの構造は, 任意の深さまで入れ子にできることに注意して下さい.
where the operands a, b, ... are MathML
expression trees themselves, and op is a MathML expression tree that
represents an operator or function. Note that apply constructs can be
nested to arbitrary depth.
applyは, 原則としていくつでも被演算子を持ちます. 例えば, (x + y + z)は次のようにコード化できます.
An apply may in principle have any number of operands. For example,
(x + y + z) can be encoded as
<apply><csymbol cd="arith1">plus</csymbol> <ci>x</ci> <ci>y</ci> <ci>z</ci> </apply>
MathMLは, 被演算子の無い関数の適用も, 例えば, random(), またはcurrent-date()のような関数を表すものも認めています.
Note that MathML also allows applications without operands, e.g. to represent functions like random(), or current-date().
演算を混合したものを意味するMathMLの式は, 入れ子になって出現するapplyとなります. 例えば, a x + bは次のようにコード化されるでしょう.
Mathematical expressions involving a mixture of operations result in nested
occurrences of apply. For example, a x + b
would be encoded as
<apply><csymbol cd="arith1">plus</csymbol>
<apply><csymbol cd="arith1">times</csymbol>
<ci>a</ci>
<ci>x</ci>
</apply>
<ci>b</ci>
</apply>式を正確に処理するために, かっこを導入したり, また, 演算子の優先順位で並び替える必要はありません. applyタグは, 他の構造の中で式を再利用するために, 適切なグループ化を提供します. apply要素で囲まれた何らかの式は, 周囲の文脈にその解釈が依存しない, 明確で密着した事象です. このことは, 同じ式が違う文脈でとても違った意味を持つかもしれないプレゼンテーションマークアップと鮮明に対比されます. 例えば, (F+G)(x)といった視覚的描画の式は, 次のような積かもしれません.
There is no need to introduce parentheses or to resort to
operator precedence in order to parse expressions correctly. The
apply tags provide the proper grouping for the re-use
of the expressions within other constructs. Any expression
enclosed by an apply element is well-defined, coherent
object whose interpretation does not depend on the surrounding
context. This is in sharp contrast to presentation markup,
where the same expression may have very different meanings in
different contexts. For example, an expression with a visual
rendering such as (F+G)(x)
might be a product, as in
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>もしくは, この式は, 関数F + Gを引数xに適用することを示しているかもしれません. この場合, 次のように和を構築することで示されます.
or it might indicate the application of the function F + G to the argument x. This is indicated by constructing the sum
<apply><csymbol cd="arith1">plus</csymbol><ci>F</ci><ci>G</ci></apply>
そして, この和が次のように引数xに適用されます.
and applying it to the argument x as in
<apply>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>F</ci>
<ci>G</ci>
</apply>
<ci>x</ci>
</apply>どちらの場合も, 外側のapplyの解釈は明確であいまいさが無く, 式がどこで使われるかに関わらず, 変わりません.
In both cases, the interpretation of the outer apply is
explicit and unambiguous, and does not change regardless of
where the expression is used.
前の例は, applyの構造の中で, 関数と引数両方とも, 単純な識別子, または, より複雑な式かもしれないことを説明しています.
The preceding example also illustrates that in an
apply construct, both the function and the arguments
may be simple identifiers or more complicated expressions.
apply要素は, 概念的に関数または演算子とそれらの利用時のデータを区別する必要があります. 関数を0以上の引数に適用することで構築される式は, いつも関数の変域内の要素です. 適切な利用方法は, 適用される演算子に依存します. 例えば, plus演算子は, 0以上の引数を持つでしょうが, minus演算子は, 適切な例とするために1つまたは2つの引数を必要とします.
The apply element is conceptually necessary in order to distinguish
between a function or operator, and an instance of its use. The expression
constructed by applying a function to 0 or more arguments is always an element from
the codomain of the function. Proper usage depends on the operator that is being
applied. For example, the plus operator may have zero or more arguments,
while the minus operator requires one or two arguments in order to be properly
formed.
4.2.5.2 関数の適用の描画
Rendering Applications
厳格なMathMLでの関数の適用は, 数学関数の適用として描画されます. が の描画を, が の描画を示しているとすると, 単純な関数の適用の描画例は, 次のようになります.
Strict Content MathML applications are rendered as mathematical
function applications. If
denotes the rendering of
and
the rendering of
, the the sample
rendering of a simple application is as follows:
コンテントMathML
Content MathML
<apply> </apply>
表示例
Sample Presentation
<mrow> <mo>⁡</mo> <mrow> <mo fence="true">(</mo> <mo separator="true">,</mo> <mo separator="true">,</mo> <mo separator="true">,</mo> <mo fence="true">)</mo> </mrow> </mrow>
厳格でないMathMLでの関数の適用は, 修飾要素と一緒に用いられることもあるでしょう. よく知られた演算子に対する何らかのより明確な描画の決まりがないことから, 描画は, sumの典型的な表現によって説明できる下記の表示例に従うべきです. は の描画であり, は の描画であるなどとします. その場合, 次のようになります.
Non-Strict MathML applications may also be used with qualifiers. In the absence of
any more specific rendering rules for well-known operators, rendering
should follow the sample presentation below, motivated by the typical
presentation for sum. Let
denote the rendering of
,
the rendering of
, and so on. Then:
コンテントMathML
Content MathML
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
表示例
Sample Presentation
<mrow> <munder> <mrow> <mo>∈</mo><!--ELEMENT OF--> </mrow> </munder> <mo>⁡</mo><!--FUNCTION APPLICATION--> <mrow> <mo fence="true">(</mo> <mo fence="true">)</mo> </mrow> </mrow>
4.2.6 束縛と束縛変数 <bind>と<bvar>
Bindings and Bound Variables <bind>
and <bvar>
たくさんの複雑な数式は, 束縛変数の利用により構築され, 束縛変数は, 論理言語や形式言語で重要な概念です. 変数は, 量化記号の利用を通して, 式の適用範囲に束縛されます. 形式ばらずに, それらは, 積分, 総和, 総積, 論理量化記号"全称記号"と"存在記号"といった式の"ダミー変数"と見なされます. 束縛変数は, 体系的に変数の名前を(式に他に現れていない名前に)変更することが, 式の意味を変更しないという特性によって特徴付けられます.
Many complex mathematical expressions are constructed with the use of bound variables, and bound variables are an important concept of logic and formal languages. Variables become bound in the scope of an expression through the use of a quantifier. Informally, they can be thought of as the "dummy variables" in expressions such as integrals, sums, products, and the logical quantifiers "for all" and "there exists". A bound variable is characterized by the property that systematically renaming the variable (to a name not already appearing in the expression) does not change the meaning of the expression.
4.2.6.1 束縛
Bindings
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Bind | Bind |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
ContExp, BvarQ*, ContExp | ContExp, BvarQ*, Qualifier*, ContExp+ |
式の束縛は, bind要素を用いたMathMLの式のツリー構造として表されます. その最初の子要素は束縛する演算子を表す, 例えば積分記号といったMathMLの式です. この後に, 束縛変数を示すbvarの空で無い一覧が続き, その最後の子要素は, 束縛される本体として知られる一般的なコンテントMathMLの式です.
Binding expressions are represented as MathML expression trees using the bind
element. Its first child is a MathML expression that represents a binding operator, for
example integral operator. This is followed by a non-empty list of bvar
elements denoting the bound variables, and then the final child which is a general
Content MathML expression, known as the body of the binding.
4.2.6.2 束縛変数
Bound Variables
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
BVar | BVar |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
ci | semantics-ci | (ci | semantics-ci), degree? | degree?, (ci | semantics-ci |
bvar要素は, 例えば, 総和, 総積, 量化記号または利用者が定義した関数の中で, 式を束縛する際の束縛変数を表すのに用いられます.
The bvar element is used to denote the bound variable of a binding
expression, e.g. in sums, products, and quantifiers or user defined functions.
bvarの中身は, 付加情報の付いた変数, すなわち, ci要素によって表されるコンテントマークアップの識別子, または, 最初の子要素が付加情報の付いた変数であるsemantics要素です. 2種類目の付加情報の付いた変数の名前は, 最初の子要素の名前です. 束縛変数の名前は, bvar要素の中の付加情報の付いた変数の名前です.
The content of a bvar element is an annotated variable,
i.e. either a content identifier represented by a ci element or a
semantics element whose first child is an annotated variable. The
name of an annotated variable of the second kind is the name of its first
child. The name of a bound variable is that of the annotated variable
in the bvar element.
束縛変数は, それらの名前を比較することで特定されます. このような特定は, bvar要素の中のci要素にidを置き, 全ての他のデータからxref属性を用いて参照することで明確にできます. この方法の例は次のとおりです.
Bound variables are identified by comparing their names. Such
identification can be made explicit by placing an id on the ci
element in the bvar element and referring to it using the xref
attribute on all other instances. An example of this approach is
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci id="var-x">x</ci></bvar>
<apply><csymbol cd="relation1">lt</csymbol>
<ci xref="var-x">x</ci>
<cn>1</cn>
</apply>
</bind>このidを基にした方法は, 束縛変数を含む構造が入れ子になっているときに, 特に助けになります.
This id based approach is especially helpful when constructions
involving bound variables are nested.
ときどき, 追加の情報を束縛変数に結び付ける必要があります. その情報は, 詳細な数学の型のようなもの, 代わりの表現やコード, 関数を適用する定義域かもしれません. そのような結び付けは, (ちょうどbvar要素の中の)ci要素を,ciと追加の情報の両方を含むsemantics要素で置き換える標準的な方法で成し遂げられます. 束縛変数のデータの評価は, それでもsemantics要素または含まれているci以外の何らかの要素ではなく, 実際のci要素に基づきます. 上で示したidに基づいた方法もまた利用できるでしょう.
It is sometimes necessary to associate additional
information with a bound variable. The information might be
something like a detailed mathematical type, an alternative
presentation or encoding or a domain of application. Such
associations are accomplished in the standard way by replacing
a ci element (even inside the bvar element)
by a semantics element containing both the ci
and the additional information. Recognition of an instance of
the bound variable is still based on the actual ci
elements and not the semantics elements or anything
else they may contain. The id based-approach
outlined above may still be used.
次の例は, forall x. x+y=y+xをコード化しています.
The following example encodes forall x. x+y=y+x.
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="relation1">eq</csymbol>
<apply><csymbol cd="arith1">plus</csymbol><ci>x</ci><ci>y</ci></apply>
<apply><csymbol cd="arith1">plus</csymbol><ci>y</ci><ci>x</ci></apply>
</apply>
</bind>厳格でないコンテントマークアップでは, bvar要素は, 数々の慣用的な構成の中で用いられます. それらについては, 第4.3.3節 修飾要素と第4.4節 具体的な演算子と定数に対するコンテントMathMLで述べています.
In non-Strict Content markup, the bvar element is used in
a number of idiomatic constructs. These are described in Section 4.3.3 Qualifiers and Section 4.4 Content MathML for Specific Operators and Constants.
4.2.6.3 束縛変数の名前の変更
Renaming Bound Variables
束縛変数の親要素であるbind要素の適用範囲の中でいつでも名前を変えられることが, 束縛変数の定義された特性です. ときどきα変換とし知られるこの操作は, 式の意味を保持します.
It is a defining property of bound variables that they can be renamed
consistently in the scope of their parent bind element.
This operation, sometimes known as α-conversion,
preserves the semantics of the expression.
束縛変数xは, そのxが束縛された範囲, またはその束縛変数xの何らかの付加情報で, 自由変数としてyが現れなければ, もしくは, yが後で現れる束縛変数でなければ, yに名前を変えることができるでしょう.
A bound variable x may be renamed to say y so long as y does not occur free in the body of the binding, or in any annotations of the bound variable, x to be renamed, or later bound variables.
束縛変数xに名前が変わる場合, bindの中のbvar要素, それに続く何らかのbvar子要素の付加情報の中や, bindの中身の式の中で, 自由変数として現れる全てのxは名前を変えられるべきです.
If a bound variable x is renamed, all free occurrences of
x in annotations in its bvar element,
any following bvar children of the bind
and in the expression in the body of the bind should be renamed.
前の節の例の中で, xをzに名前を変更することが, どのように等価な式forall z. z+y=y+zが提供されるか注意して下さい. 一方で, 束縛された範囲の中でyが自由変数として入力されるかもしれず, 元の式と等価でない式forall y. y+y=y+yを提供することから, xはyに名前を変更できないことに注意して下さい.
In the example in the previous section, note how renaming x to z produces the equivalent expression forall z. z+y=y+z, whereas x may not be renamed to y, as y is free in the body of the binding and would be captured, producing the expression forall y. y+y=y+y which is not equivalent to the original expression.
4.2.6.4 束縛する構成の描画
Rendering Binding Constructions
と がプレゼンテーションMathMLの式 と を描画するコンテントMathMLの式である場合, 束縛する要素の描画例は次のとおりです.
If
and
are Content MathML expressions
that render as the Presentation MathML expressions
and
then the sample rendering of a binding element is as follows:
コンテントMathML
Content MathML
<bind> <bvar> </bvar> <bvar> </bvar> <bvar> </bvar> </bind>
表示例
Sample Presentation
<mrow> <mrow> <mo separator="true">,</mo> <mo separator="true">,</mo> </mrow> <mo separator="true">.</mo> </mrow>
4.2.7 構造の共有 <share>
Structure Sharing <share>
XMLコードの中の領域を保つために, MathMLの式のツリー構造は, 構造の共有を利用することができます.
To conserve space in the XML encoding, MathML expression trees can make use of structure sharing.
4.2.7.1 share要素
The share element
| 構文 Schema Fragment |
|
|---|---|
| 種類 Class |
Share |
| 属性 Attributes |
CommonAtt, src |
src属性の値src Attribute Values
|
URI |
| 内容 Content |
なし Empty |
share要素は, MathMLの式のツリー構造を参照するのに使われるhref属性を持っています. href属性の値は, 式のツリー構造のルート要素のid属性を指定するURIです. MathMLの式のツリー構造を組み立てるとき, share要素は, href属性で参照したMathMLの式のツリー構造のコピーと等価です. このコピーは構造的に等しいが, 参照されている要素と同一ではないことに注意して下さい. shareの値は, よく相対的なURI参照となり, その場合, share要素を含む文書の基となるURIを利用して解決されます.
The share element has an href attribute used to
to reference a MathML expression tree. The value of the
href attribute is a URI specifying the id
attribute of the root node of the expression tree. When building a
MathML expression tree, the share element is equivalent to a copy of the MathML
expression tree referenced by the href attribute. Note that this copy is
structurally equal, but not identical to the element referenced. The
values of the share will often be relative URI references, in which case they
are resolved using the base URI of the document containing the share element.
例えば, 数学的事象f(f(f(a,a),f(a,a)),f(f(a,a),f(a,a)))は, 次に示す表現のいずれか1つとして(さらにそれらの中間的な形として)コード化できます.
For instance, the mathematical object f(f(f(a,a),f(a,a)),f(f(a,a),f(a,a))) can be encoded as either one of the following representations (and some intermediate versions as well).
<apply><ci>f</ci>
<apply><ci>f</ci>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply>
<apply><ci>f</ci>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<apply><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
</apply>
</apply>
|
<apply><ci>f</ci>
<apply id="t1"><ci>f</ci>
<apply id="t11"><ci>f</ci>
<ci>a</ci>
<ci>a</ci>
</apply>
<share href="#t11"/>
</apply>
<share href="#t1"/>
</apply>
|
4.2.7.2 非循環の制限
An Acyclicity Constraint
ある要素が, その子要素とそれらを構成している全ての要素から成り立っているとします. また, share要素がその対象, すなわちhref属性によって示されたid属性を持つ要素から成り立っているとします. 例えば, 前に示した右の表現において, id="t1"のapply要素と, (href="t11"の)2番目のshareの両方が, id="t11"のapply要素から成り立っています.
Say that an element dominates all its children and all
elements they dominate. Say also that a
share element dominates its target, i.e. the element that carries the
id attribute pointed to by the href attribute. For instance in the
representation on the right above, the apply element with id="t1" and also the
second share (with href="t11") both dominate the
apply element with id="t11".
share要素の出現は, 次に示す全体の非循環の制限に従わなければなりません. 要素は, 自分自身を含むことができないでしょう. 例えば, 次の表現は, この制限に違反しています.
The occurrences of the share element must obey the following global
acyclicity constraint: An element may not dominate itself. For example, the
following representation violates this constraint:
<apply id="badid1"><csymbol cd="arith1">divide</csymbol>
<cn>1</cn>
<apply><csymbol cd="arith1">plus</csymbol>
<cn>1</cn>
<share href="#badid1"/>
</apply>
</apply>ここで, id="badid1"のapply要素は, id="badid1"の要素を対象とするshare要素から成り立っている3番目の子要素から成り立っています. そのため, 変換によってこの要素は自分自身から成り立っています. 非循環の制限によって, この例は, 有効なMathMLの式のツリー構造ではありません. 連分数 の解釈としてそのような式が与えられるだろうと主張されるかもしれません. ただし,
の解釈としてそのような式が与えられるだろうと主張されるかもしれません. ただし, share要素を置き換えることによって, 式のツリー構造を組み立てる方法は, そのような式を終わらせず, よって, そのような式はコンテントMathMLによって認められていません.
Here, the apply element with id="badid1" dominates its third child,
which dominates the share element, which dominates its target: the element with
id="badid1". So by transitivity, this element dominates itself. By the
acyclicity constraint, the example is not a valid MathML expression tree. It
might be argued that such an expression could be given the interpretation of the continued fraction
 .
However, the procedure of building an expression tree by replacing
.
However, the procedure of building an expression tree by replacing
share element does not terminate for such an
expression, and hence such expressions are not allowed by Content MathML.
非循環の制限は, そのような単純な場合に限定されず, 次の例のように示される場合もあることに注意して下さい.
Note that the acyclicity constraints is not restricted to such simple cases, as the following example shows:
<apply id="bar"> <apply id="baz"> <csymbol cd="arith1">plus</csymbol> <csymbol cd="arith1">plus</csymbol> <cn>1</cn> <cn>1</cn> <share href="#baz"/> <share href="#bar"/> </apply> </apply>
ここで, id="bar"のapplyは, その3番目の子要素, href="#baz"のshareから成り立っています. この要素は, その対象である, 今度は自身の3番目の子要素としてhref="#bar"のshareを含んでいる(id="baz"の)applyから成り立っています. 最終的に, href="#bar"のshareは, その対象であるid="bar"の元々のapplyから成り立っています. そのため, この表現の組は, 結局は非循環の制限に違反しています.
Here, the apply with id="bar" dominates its third child, the
share with href="#baz". That element dominates its target apply
(with id="baz"), which in turn dominates its third child, the share
with href="#bar". Finally, the share with
href="#bar" dominates its target, the original
apply element with id="bar". So this pair of representations
ultimately violates the acyclicity constraint.
4.2.7.3 共有と束縛の構造
Structure Sharing and Binding
share要素は, 構文上の参照の仕組みであることに注意して下さい. share要素は, それが差し示す実際の要素としてふるまいます. 特に, 参照は, 変数の捕捉と呼ばれる現象が起こることを認めているので, 意味的に直観的な方法では束縛と相互作用しません. 次の例を考えます.
Note that the share element is a syntactic referencing mechanism:
a share element stands for the exact element it points to. In particular,
referencing does not interact with binding in a semantically intuitive way, since it
allows a phenomenon called variable capture to
occur. Consider an example:
<bind id="outer"><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><ci>f</ci>
<bind id="inner"><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<share id="copy" href="#orig"/>
</bind>
<apply id="orig"><ci>g</ci><ci>x</ci></apply>
</apply>
</bind>この例は, 式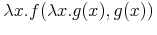 を表しており, この式は,
を表しており, この式は, 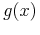 から成る2つの項, (はっきりと表現されている)
から成る2つの項, (はっきりと表現されている)id="orig"のものと, share要素によって表現されているid="copy"のものを持ちます. 元々のはっきりと表現されている項において, 変数xは外側の bind要素により束縛されています. しかしながら, コピーの方では, 変数xは内側の bind要素によって束縛されています. ここで, 内側のbindは, 変数xを補足していると言われます.
This represents a term
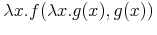 which has two sub-terms of the form
which has two sub-terms of the form
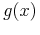 ,
one with
,
one with id="orig"
(the one explicitly represented) and one with id="copy",
represented by the share element.
In the original, explicitly-represented term,
the variable x is bound by the
outer bind element.
However, in the copy, the variable x is
bound by the inner bind element.
One says that the inner bind
has captured the variable x.
この方法で意味を補足する参照の利用は, 簡単に表示のエラーに結び付き, 推奨されません. 例えば, α変換を利用して内側に現れるxをyに名前を変えることは, 意味的に等価な式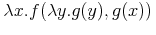 を生み出します. しかしながら, この形式において, もはや式
を生み出します. しかしながら, この形式において, もはや式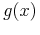 を共有することはできません.
を共有することはできません. share要素を置き換えること無しに, 内側のbvarのxをyに置き換えることは, 意味の上で変更したことになります.
Using references that capture variables in this way can easily lead to representation
errors, and is not recommended. For instance, using
α-conversion to rename the inner occurrence of x
into, say, y leads to the semantically equivalent expression
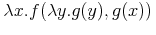 .
However, in this form, it is no longer possible to share the expression
.
However, in this form, it is no longer possible to share the expression
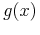 .
Replacing x with y in the inner
.
Replacing x with y in the inner
bvar without replacing the share element results in a change
in semantics.
4.2.7.4 構造を共有した式の描画
Rendering Expressions with Structure Sharing
share要素に対するいくつかの無難な描画があります. それらの描画は, 参照された要素へのハイパーリンクとして要素を描画することや, href属性により参照されている要素の描画を用いることが含まれます.
There are several acceptable renderings for the share element. These include rendering the element
as a hypertext link to the referenced element and using the rendering of the element referenced by the
href attribute.
4.2.8 semanticsによる付加情報
Attribution via semantics
コンテント要素は, semantics要素によって追加の情報を付加されるでしょう. MathMLは, semantics要素を, 付加される要素と, 付加情報自体を表しているannotation-xmlとannotationを包み込むのに用います. semantics, annotation, annotation-xmlの利用については, 第5章 数式に対するマークアップ言語の混在で詳しく説明しています.
Content elements can be annotated with additional information via the
semantics element. MathML uses the
semantics element to wrap the annotated element and the
annotation-xml and annotation elements used for representing the
annotations themselves. The use of the semantics, annotation and
annotation-xml is described in detail Chapter 5 Mixing Markup Languages for Mathematical Expressions.
semantics要素は, プレゼンテーションMathMLとコンテントMathMLの両方の一部と見なされています. MathMLは, semantics要素の最初の子要素が(厳格な)コンテントMathMLであるなら, そのsemantics要素を(厳格な)コンテントMathMLと見なします.
The semantics element is be considered part of both
presentation MathML and Content MathML. MathML considers a semantics element
(strict) Content MathML, if and only if its first child is (strict) Content MathML.
4.2.9 エラーマークアップ <cerror>
Error Markup <cerror>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Error | Error |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
csymbol, ContExp* | csymbol, ContExp* |
コンテントMathMLのエラー表現は, csymbolとそれに続く0個以上の一連のMathMLの式で作られます. 最初の式は, エラーの種類を示すcsymbolでなければなりません. その後の一連の子要素は, 存在するなら, エラーが起こった文脈を示します.
A content error expression is made up of a csymbol
followed by a sequence of zero or more MathML expressions. The
initial expression must be a csymbol indicating the kind of
error. Subsequent children, if present, indicate the context in
which the error occurred.
cerror要素は, 直接の数学的意味を持ちません. 式のツリー構造において行われた何らかの動作の結果としてエラーが起こったとき, 何らかのエラーが, いつ起こったかのみが実際に注目されます. エラーは, 他の事象の中で起こったかもしれず, また, 他のエラーの中で起こったかもしれません.
The cerror element has no direct mathematical meaning.
Errors occur as the result of some action performed on an expression
tree and are thus of real interest only when some sort of
communication is taking place. Errors may occur inside other objects
and also inside other errors.
例えば, ゼロ除算エラーをコード化するために, 次に示す式のように, DivisionByZero記号を含むaritherrorコンテント辞書を使用するとします.
As an example, to encode a division by zero error, one might
employ a hypothetical aritherror Content Dictionary
containing a DivisionByZero symbol, as in the following
expression:
<cerror> <csymbol cd="aritherror">DivisionByZero</csymbol> <apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply> </cerror>
エラーのマークアップは, 一般に最小限の間違った式のみを囲むべきであることに注意して下さい. よって, cerrorは大きな式の一部の式にたびたびなります. 例えば, 次のようにです.
Note that error markup generally should enclose only the smallest
erroneous sub-expression. Thus a cerror will often be a sub-expression of
a bigger one, e.g.
<apply><csymbol cd="relation1">eq</csymbol>
<cerror>
<csymbol cd="aritherror">DivisionByZero</csymbol>
<apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply>
</cerror>
<cn>0</cn>
</apply>cerror要素の通常の表現は, 最初の子要素がエラー記号を表し, その後の一連の子要素が, cerrorの残りの子要素の通常の表現を表す, merrorの式です. 特に, cerrorの残りの子要素の一部がプレゼンテーションMathMLの式であるなら, 文字どおりmerrorに囲まれた中で使用されるでしょう.
The default presentation of a cerror element is an
merror expression whose first child is a presentation of the
error symbol, and whose subsequent children are the default
presentations of the remaining children of the cerror. In
particular, if one of the remaining children of the cerror is
a presentation MathML expression, it is used literally in the
corresponding merror.
<cerror> <csymbol cd="aritherror">DivisionByZero</csymbol> <apply><csymbol cd="arith1">divide</csymbol><ci>x</ci><cn>0</cn></apply> </cerror>
表示例
Sample Presentation
<merror> <mtext>DivisionByZero: </mtext> <mfrac><mi>x</mi><mn>0</mn></mfrac> </merror>
エラーが起こった文脈が無意味で, その通常の表現が使い勝手が悪い場合, ソフトウェアはエラーの文脈の代わりの表現を提供するかもしれません. 例えば, 次のようにです.
Note that when the context where an error occurs is so nonsensical that its default presentation would not be useful, an application may provide an alternative representation of the error context. For example:
<cerror> <csymbol cd="error">Illegal bound variable</csymbol> <cs> <bvar><plus/></bvar> </cs> </cerror>
4.2.10 コード化されたバイト列 <cbytes>
Encoded Bytes <cbytes>
| (厳格な)構文 Schema Fragment (Strict) |
(完全な)構文 Schema Fragment (Full) |
|
|---|---|---|
| 種類 Class |
Cbytes | Cbytes |
| 属性 Attributes |
CommonAtt | CommonAtt, DefEncAtt |
| 内容 Content |
base64 | base64 |
cbytesの中身は, Base64でコード化された一連の文字列としてバイト列を表します. これは, [XMLスキーマデータ型]で定義されたbase64Binaryデータ型と一致します. 全ての空白は無視されます.
The content of cbytes represents a stream of bytes as a
sequence of characters in Base64 encoding, that is it matches the
base64Binary data type defined in [XMLSchemaDatatypes]. All white space is ignored.
cbytes要素は, 主にOpenMathとの互換性のために利用されますが, OpenMathでのように, MathMLでコード化するのが難しい, ソフトウェアの内部状態に関係したバイナリデータや画像データといったソフトウェアの出力を包み込むために利用されるかもしれません.
The cbytes element is mainly used for OpenMath
compatibility, but may be used, as in OpenMath, to encapsulate output
from a system that may be hard to encode in MathML, such as binary
data relating to the internal state of a system, or image data.
cbytesの描画は, 内容を表すことが期待されておらず, 提案されている描画は, 空のmrowです. 典型的にcbytesは, annotation-xmlの中で使用されたり, プレゼンテーションMathMLに付加されたりするので, 通常の描画は稀に利用されるべきです.
The rendering of cbytes is not expected to represent the
content and the proposed rendering is that of an empty
mrow. Typically cbytes is used in an
annotation-xml or is itself annotated with Presentation
MathML, so this default rendering should rarely be used.
4.3 具体的な構造に対するコンテントMathML
Content MathML for Specific Structures
前の節で説明した厳格なコンテントMathMLの要素は, 論理的主張や式の構造をコード化するのに十分であり, 数学の基礎となる数学論理の標準構造を綿密に形作る方法によってコード化します. 結果として, 厳格なマークアップは, 数学の全てを表現するのに利用でき, 全てのコンテントMathMLの式に一貫した数学的意味を提供するのに理想的です.
The elements of Strict Content MathML described in the previous section are sufficient to encode logical assertions and expression structure, and they do so in a way that closely models the standard constructions of mathematical logic that underlie the foundations of mathematics. As a consequence, Strict markup can be used to represent all of mathematics, and is ideal for providing consistent mathematical semantics for all Content MathML expressions.
同時に, たくさんの数学の自然な表記方法は, 厳格なコンテントMathMLで直接表現するには, すっきりリしたものではありません. 例えば, 総和, 積分, 集合, 区分的関数や他の一般的な構造のための標準的な表記方法は, 厳格なマークアップを用いて厳密にコード化しようとすると, ラムダ関数の導入といった技術的な工夫が必要です. 結果として, コンテントMathMLを使いやすくするためには, 追加の要素の集合が, そのような慣用的な構造をより直接コード化するために提供されます. この節では, そのような慣用的な構造を一般的な利用形式やそれらと等価な厳格なコンテントMathMLについて議論しています. 特定の構成は, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで詳細を議論しています.
At the same time, many notational idioms of mathematics are not straightforward to represent directly with Strict Content markup. For example, standard notations for sums, integrals, sets, piecewise functions and many other common constructions require non-obvious technical devices, such as the introduction of lambda functions, to rigorously encode them using Strict markup. Consequently, in order to make Content MathML easier to use, a range of additional elements have been provided for encoding such idiomatic constructs more directly. This section discusses the general approach for encoding such idiomatic constructs, and their Strict Content equivalents. Specific constructions are discussed in detail in Section 4.4 Content MathML for Specific Operators and Constants.
コンテントMathMLが処理するほとんどの慣用的な構造は, たくさんの種類に及びます. 入れ物要素といったように, それらの種類の中には, 固有の構文を持っているものもあります. 同じように, 厳格でない構造の中には少し, 例えばpartialdiffといった例外的な構文を持つ単独の要素も含まれます. それらの例外的な要素は, 第4.4節 具体的な演算子と定数に対するコンテントMathMLの中で状況に応じて議論されています. しかしながら, 構造の大部分は, 全て修飾要素の個々の利用で共通の演算子要素の種類から成ります. それらの演算子の種類は, 第4.3.4節 演算子の種類で説明されています.
Most idiomatic constructions which Content markup addresses fall
into about a dozen classes. Some of these classes, such as container elements, have
their own syntax. Similarly, a small number of non-Strict
constructions involve a single element with an exceptional syntax,
for example partialdiff. These exceptional elements are
discussed on a case-by-case basis in Section 4.4 Content MathML for Specific Operators and Constants. However, the majority of constructs consist of
classes of operator elements which all share a particular usage of
qualifiers.
These classes of operators are described in Section 4.3.4 Operator Classes.
全ての場合に, 厳格でない式は, 厳格なマークアップのみを用いて書き換えられるでしょう. 変換は, 完全にアルゴリズムとして確立されており, 自動で行われるかもしれません. 厳格でないマークアップの情報に対する書き換えの決まりは, この節の後の方で紹介し議論しています. 単独の要素を含む例外的な構造に対する書き換えの決まりは, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで示されています. 任意のコンテントMathMLを厳格なコンテントマークアップに書き換えるための完全なアルゴリズムは, この章の最後, 第4.6節 厳格なコンテントMathMLへの変換の中で要約されています.
In all cases, non-Strict expressions may be rewritten using only Strict markup. In most cases, the transformation is completely algorithmic, and may be automated. Rewrite rules for classes of non-Strict constructions are introduced and discussed later in this section, and rewrite rules for exceptional constructs involving a single operator are given in Section 4.4 Content MathML for Specific Operators and Constants. The complete algorithm for rewriting arbitrary Content MathML as Strict Content markup is summarized at the end of the Chapter in Section 4.6 The Strict Content MathML Transformation.
4.3.1 入れ物マークアップ
Container Markup
たくさんの数学構造が, 部分的な式や変数によって構築されています. 刺激的な例は集合です. 形式ばらずに, 一連の要素を含む数学事象の種類を集合と考えるでしょう. よって, 集合のマークアップにとって, XMLの意味合いで, 集合を構築している要素に対するマークアップを含んでいるのが直観的に自然です. マークアップは, 含んでいる要素を列挙したり, 暗に決まりに従って修飾要素を使用したりすることで, 集合要素を定義するかもしれません. ただし, どちらの場合も, 要素に対するマークアップは, 集合に対するマークアップの中に含まれ, 結果として, この表現の形式は, MathMLにおける入れ物マークアップと呼ばれます. 対照的に厳格なマークアップは, 集合のデータを, 関数または構築子記号を引数に適用した結果として表します. 厳格なマークアップの形式では, 集合構造に対するマークアップは, 囲っているapply要素の中の集合要素に対するマークアップの兄弟要素です.
Many mathematical structures are constructed from subparts or
parameters. The motivating example is a set. Informally, one
thinks of a set as a certain kind of mathematical object that
contains a collection of elements. Thus, it is intuitively natural
for the markup for a set to contain, in the XML sense, the markup
for its constituent elements. The markup may define the set
elements explicitly by enumerating them, or implicitly by rule,
using qualifier elements. However, in either case, the markup for
the elements is contained in the markup for the set, and
consequently this style of representation is termed
container markup in MathML. By contrast, Strict
markup represents an instance of a set as the result of applying a
function or constructor symbol to arguments. In this
style of markup, the markup for the set construction is a sibling
of the markup for the set elements in an enclosing apply
element.
2つの手法が正式に等価であるにも関わらず, 入れ物マークアップは, 一般に, 熟練していない利用者にとって, 利用するのにより直観的です. 厳格なマークアップが, 意味的な厳格さが最大限必要な文脈では好ましいにも関わらずです. 加えて, MathML2は, 入れ物マークアップに頼っていて, そのため, 入れ物マークアップは, 下位互換性が必要な場合に必要です.
While the two approaches are formally equivalent, container markup is generally more intuitive for non-expert authors to use, while Strict markup is preferable is contexts where semantic rigor is paramount. In addition, MathML 2 relied on container markup, and thus container markup is necessary in cases where backward compatibility is required.
MathMLは, 次の数学構造, 集合, リスト, 区間, ベクトル, 行列(2つの要素), 区分的関数(3つの要素), ラムダ関数に対する入れ物マークアップを提供します. 厳格なマークアップの束縛記号に対応するラムダ関数を除いて, それら入れ物マークアップの1つ1つに対応する厳格なマークアップの構築子記号があります. MathML2では, "入れ物マークアップ"という用語は, 素子要素, 非推奨のdeclare, fn, relnを含んでいましたが, MathML3は, その用語の利用を上で示した構造に限定しています.
MathML provides container markup for the following mathematical
constructs: sets, lists, intervals, vectors, matrices (two
elements), piecewise functions (three elements) and lambda
functions. There are corresponding constructor symbols in Strict
markup for each of these, with the exception of lambda functions,
which correspond to binding symbols in Strict markup. Note that in
MathML 2, the term "container markup" was also taken to include
token elements, and the deprecated declare, fn
and reln elements, but MathML 3 limits usage of the term
to the above constructs.
入れ物マークアップから等価な厳格なコンテントマークアップを得る書き換えの決まりは, 含まれている個々の演算子の種類に依存します. 特定の入れ物マークアップの詳細について, 第4.4節 具体的な演算子と定数に対するコンテントMathMLでの, その要素に対する構文の表や議論を調べることで, 演算子の種類(や何らかの適用可能な特別な状況の情報)を付けられます. そして, 第4.3.4節 演算子の種類で説明されている具体的な演算子の種類に対する書き換えの決まりが適用されます.
The rewrite rules for obtaining equivalent Strict Content markup from container markup depend on the operator class of the particular operator involved. For details about a specific container element, obtain its operator class (and any applicable special case information) by consulting the syntax table and discussion for that element in Section 4.4 Content MathML for Specific Operators and Constants. Then apply the rewrite rules for that specific operator class as described in Section 4.3.4 Operator Classes.
4.3.1.1 構築要素の記号に対する入れ物マークアップ
Container Markup for Constructor Symbols
構築要素に対応する入れ物要素の引数は, 一連の子要素として明確に与えられるか, 修飾要素を利用する決まりによって特定されるかのどちらかです. 例外は, 区分的定義を伴う関数で利用されるpiecewise, piece, otherwise要素のみです. それらの要素の引数は, いつも明確に指定されなければなりません.
The arguments to container elements corresponding to
constructors may either be explicitly given as a sequence of child
elements, or they may be specified by a rule using qualifiers. The
only exceptions are the piecewise, piece, and
otherwise elements used for representing functions with
piecewise definitions. The
arguments of these elements must always be specified
explicitly.
ここに, 明確に指定された引数を含む入れ物マークアップの例があります.
Here is an example of container markup with explicitly specified arguments:
<set><ci>a</ci><ci>b</ci><ci>c</ci></set>
この式は, 次の厳格なコンテントMathMLの式と等価です.
This is equivalent to the following Strict Content MathML expression:
<apply><csymbol cd="set1">set</csymbol><ci>a</ci><ci>b</ci><ci>c</ci></apply>
入れ物マークアップの他の例があります. 引数の一覧は, 間接的に束縛変数の式として与えられます. 偶数の集合に対する入れ物マークアップは次のとおりです.
Another example of container markup, where the list of arguments is given indirectly as an expression with a bound variable. The container markup for the set of even integers is:
<set> <bvar><ci>x</ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><times/><cn>2</cn><ci>x</ci></apply> </set>
この式は, 厳格なコンテントMathMLで次のように書き換えられます.
This may be written as follows in Strict Content MathML:
<apply><csymbol cd="set1">map</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="arith1">times</csymbol>
<cn>2</cn>
<ci>x</ci>
</apply>
</bind>
<csymbol cd="setname1">Z</csymbol>
</apply>4.3.1.2 束縛する構築要素に対する入れ物マークアップ
Container Markup for Binding Constructors
lambda要素は, fns1コンテント辞書のlambda記号に対応する入れ物要素です. しかしながら, 前の節の入れ物要素と異なり, 引数から数学事象を純粋に構築するlambda要素は, 束縛変数としてふるまいます. よって, lambdaの子要素は, 別々の役割を持っています. 特に, lambda要素は, 最終的に, 1つのbvar子要素, それに続く必須でない修飾要素, それに続くコンテントMathML要素を持たなければなりません. lambda入れ物要素と他の構築子入れ物要素の基本的な違いは, それらの対応するOpenMath記号に反映されています. 構築子記号は, "関数の適用"のOpenMathの役割を持っている一方, ラムダ記号は, "束縛"の役割を持っています.
The lambda element is a container element
corresponding to the lambda symbol
in the fns1 Content Dictionary. However, unlike the
container elements of the preceding section, which purely
construct mathematical objects from arguments, the lambda
element performs variable binding as well. Therefore, the child
elements of lambda have distinguished roles. In
particular, a lambda element must have at least one
bvar child, optionally followed by qualifier elements, followed by a
Content MathML element. This basic difference between the
lambda container and the other constructor container
elements is also reflected in the OpenMath symbols to which they
correspond. The constructor symbols have an OpenMath role of
"application", while the lambda symbol has a role of "bind".
次の例は, lambda入れ物要素の使用方法と厳格なコンテント要素で等価なbindの使用方法を示しています.
This example shows the use of lambda container element and the equivalent use of bind in Strict Content MathML
<lambda><bvar><ci>x</ci></bvar><ci>x</ci></lambda>
<bind><csymbol cd="fns1">lambda</csymbol> <bvar><ci>x</ci></bvar><ci>x</ci> </bind>
4.3.2 <apply>による束縛
Bindings with <apply>
MathMLは, bind要素の代わりに厳格でない構造で, 変数を束縛するように働くapply要素の利用を認めています. この利用方法は, MathML2との下位互換性を維持するものです. このことは, 後で示すように束縛変数と修飾要素を伴ういくつかの構造をコード化するのを単純にします.
MathML allows the use of the apply element to perform
variable binding in non-Strict constructions instead of
the bind element. This usage conserves backwards
compatibility with MathML 2. It also simplifies the encoding of
several constructs involving bound variables with qualifiers as
described below.
変数を束縛するのにapply要素を利用することは, 2つの場合に認められています. 1つは, 適用する演算子が束縛する演算子自体のときで, apply要素は単にbind要素の代わりに用いられます. 論理量化要素<forall/>, <exists/>, 入れ物要素lambdaが, この形式の主な例です.
Use of the apply element to bind variables is allowed
in two situations. First, when the operator to be applied is
itself a binding operator, the apply element merely
substitutes for the bind element. The logical quantifiers
<forall/>, <exists/> and the
container element lambda are the primary examples of this
type.
2つ目は, 適用される演算子が修飾要素と一緒に束縛変数を利用することを認めている場合です. 最も一般的な例は, 総和と積分です. それらの場合のほとんどで, 変数は, 表記の中で暗黙のうちに何らかの範囲に束縛され, 等価な厳格な表現は, 形式の正しさのために, ラムダ式といった補助的な構造を必要とします.
The second situation arises when the operator being applied allows the use of bound variables with qualifiers. The most common examples are sums and integrals. In most of these cases, the variable binding is to some extent implicit in the notation, and the equivalent Strict representation requires the introduction of auxiliary constructs such as lambda expressions for formal correctness.
修飾要素と一緒に束縛変数を利用する式は, 通常慣用的で, いつも本当に変数を束縛している訳ではないので, 全ての場合に表記を維持したまま, applyと一緒の"束縛"変数の定型的な名前の変更(アルファ変換)が期待できます. この場合の例としては, bvarの項が技術的に全く束縛されていないdiff要素があります.
Because expressions using bound variables with qualifiers are
idiomatic in nature, and do not always involve true variable
binding, one cannot expect systematic renaming (alpha-conversion)
of variables "bound" with apply to preserve meaning in
all cases. An example for this is the diff element where
the bvar term is technically not bound at all.
次の例は, 束縛する演算子と一緒にapplyを利用する例を説明しています. これらの場合において, 対応する等価な厳格な表現は, 単にapply要素をbind要素で置き換えます.
The following example illustrates the use of apply
with a binding operator. In these cases, the corresponding Strict
equivalent merely replaces the apply element with a
bind element:
<apply><forall/> <bvar><ci>x</ci></bvar> <apply><geq/><ci>x</ci><ci>x</ci></apply> </apply>
対応する等価な厳格な表現は次のとおりです.
The equivalent Strict expression is:
<bind><csymbol cd="logic1">forall</csymbol> <bvar><ci>x</ci></bvar> <apply><csymbol cd="relation1">geq</csymbol><ci>x</ci><ci>x</ci></apply> </bind>
この例では, sum演算子自体は束縛する演算子ではありませんが, 修飾要素と一緒の束縛変数は, 厳格でないマークアップで反映された標準的な表記の中で暗黙のものです. 等価な厳格な表現は, 被加数をラムダ式に変換し, 修飾要素を引数の式として役割を変える必要があります.
In this example, the sum operator is not itself a binding operator, but bound variables with qualifiers are implicit in the standard notation, which is reflected in the non-Strict markup. In the equivalent Strict representation, it is necessary to convert the summand into a lambda expression, and recast the qualifiers as an argument expression:
<apply><sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
対応する等価な厳格な表現は次のとおりです.
The equivalent Strict expression is:
<apply><csymbol cd="arith1">sum</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol>
<ci>x</ci>
<ci>i</ci>
</apply>
</bind>
</apply>4.3.3 修飾要素
Qualifiers
たくさんの一般的な数学的構造は, 演算子と一緒に追加の情報を含んでいます. 追加の情報は, 束縛変数といった従来の表記法に暗に含まれるか, 定積分の範囲の場合のように演算子の一部と思われているかのどちらかです. MathML3は, 修飾要素を, このような場合に追加の情報を表現するために使用します.
Many common mathematical constructs involve an operator together with some additional data. The additional data is either implicit in conventional notation, such as a bound variable, or thought of as part of the operator, as is the case with the limits of a definite integral. MathML 3 uses qualifier elements to represent the additional data in such cases.
修飾要素は, いつも演算子や入れ物要素と結び付けられて使用されます. それらの意味は慣用的で, 使用される文脈に依存します. 演算子と一緒に用いられる場合, 修飾要素は, いつも演算子の後に続き, 存在するどの引数より前に来ます. 全ての場合において, 複数の修飾要素が存在する場合, それらは, bvar, lowlimit, uplimit, interval, condition, domainofapplication, degree, momentabout, logbaseの順で現れます.
Qualifier elements are always used in conjunction with operator or container
elements. Their meaning is idiomatic, and depends on the context in which they are
used. When used with an operator, qualifiers always follow the operator and precede
any arguments that are present. In all cases, if more than one qualifier is present,
they appear in the order bvar, lowlimit, uplimit,
interval, condition, domainofapplication, degree,
momentabout, logbase.
修飾要素の正確な機能は, それらが修飾している演算子や入れ物要素に依存します. 使用例の大半は, 後で議論するいくつかの種類のうちの1つに落とし込めます. そして, 具体的な演算子や修飾要素に対する利用上の注意は, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで示されています.
The precise function of qualifier elements depends on the operator or container that they modify. The majority of use cases fall into one of several categories, discussed below, and usage notes for specific operators and qualifiers are given in Section 4.4 Content MathML for Specific Operators and Constants.
4.3.3.1 <domainofapplication>, <interval>, <condition>, <lowlimit>, <uplimit>の利用
Uses of
<domainofapplication>,
<interval>,
<condition>,
<lowlimit> and
<uplimit>
| 種類 Class |
qualifier |
|---|---|
| 属性 Attributes |
CommonAtt |
| 内容 Content |
ContExp |
(intervalの構文については, 第4.4.1.1節 範囲 <interval>を参照して下さい.)
(For the syntax of interval see Section 4.4.1.1 Interval <interval>.)
domainofapplication, interval, uplimit, lowlimit, conditionの主な利用目的は, 束縛変数の値を限定することです. 最も一般的な修飾要素は, domainofapplicationです. この要素は, 演算が行われる上での(場合によっては, 順番や測定基準といった追加の構造を持つ)集合を指定するのに用いられます. interval修飾要素や, lowlimitとuplimitの組みは, 特別な場合として, 束縛変数をそれらの組が表す区間内に制限します. condition修飾要素は, domainofapplicationのように, 一般的な要素で, 束縛変数を任意の集合の中に制限するのに利用できます. ただし, 他の修飾要素とは異なり, この要素は, 束縛変数に対するブール値の関数を指定することで, 束縛変数を制限します. よって, condition修飾要素は, いつも束縛変数のデータを含んでおり, 他の修飾要素では必要のない前に来るbvarを必要とします. 他の修飾要素は, 例えば, 関数の定義域を一部に制限するといった, 変数が何ら束縛されていない時にさえ利用されるでしょう.
The primary use of domainofapplication, interval,
uplimit, lowlimit and condition is to
restrict the values of a bound variable. The most general qualifier
is domainofapplication. It is used to specify a set (perhaps
with additional structure, such as an ordering or metric) over which
an operation is to take place. The interval qualifier, and
the pair lowlimit and uplimit also restrict a bound
variable to a set in the special case where the set is an
interval. The condition qualifier, like
domainofapplication, is general, and can be used to restrict
bound variables to arbitrary sets. However, unlike the other
qualifiers, it restricts the bound variable by specifying a
Boolean-valued function of the bound variable. Thus,
condition qualifiers always contain instances of the bound
variable, and thus require a preceding bvar, while the other
qualifiers do not. The other qualifiers may even be used when no
variables are being bound, e.g. to indicate the restriction of a
function to a subdomain.
ほとんどの場合に, 影響範囲を表現できるどの修飾要素も, 交換可能なものとして利用されています. 最も一般的な修飾要素はdomainofapplicationで, そのため特別な役割を持っています. この要素は, 例えば積分の極限といった他の修飾要素の1つを利用する特に慣用的な理由が無い限り, 好ましい形式です. MathML3では, 他の形式は, それらが全て等価なdomainofapplicationの構造に書き換えられることから, domainofapplicationの簡潔な表記として扱われます. この書き換えの決まりは後で示します. 他の修飾要素は, 一般的な表記に合致し, よく知られた用語により簡単に結び付くことから提供されています. よって, それらの要素が自然に現れる状況では, それらの要素は, domainofapplicationより便利で直接的でしょう.
In most cases, any of the qualifiers capable of representing the
domain of interest can be used interchangeably. The most general
qualifier is domainofapplication, and therefore has a
privileged role. It is the preferred form, unless there are
particular idiomatic reasons to use one of the other qualifiers,
e.g. limits for an integral. In MathML 3, the other forms are treated
as shorthand notations for domainofapplication because they
may all be rewritten as equivalent domainofapplication
constructions. The rewrite rules to do this are given below. The other
qualifier elements are provided because they correspond to common
notations and map more easily to familiar presentations. Therefore,
in the situations where they naturally arise, they may be more
convenient and direct than domainofapplication.
この考え方を説明するために, 定積分の代わりの表現を示す次の例を考えます. Cは0から1までの区間を表し, f(x) = x2です. このとき, domainofapplicationは, 区間Cでの関数fの積分を次の形で表すように用いられます.
To illustrate these ideas, consider the following examples showing alternative
representations of a definite integral. Let C denote the interval from 0 to 1,
and f(x) = x2. Then
domainofapplication could be used express the integral of a
function f over
C in this way:
<apply><int/>
<domainofapplication>
<ci type="set">C</ci>
</domainofapplication>
<ci type="function">f</ci>
</apply>このコードの中に何ら明確な束縛変数は確認されず, 被積分関数は関数の表記であることに注意して下さい. その代わりに, interval修飾要素は, 明確な束縛変数を伴って用いられます.
Note that no explicit bound variable is identified in this
encoding, and the integrand is a function. Alternatively, the
interval qualifier could be used with an explicit bound variable:
<apply><int/> <bvar><ci>x</ci></bvar> <interval><cn>0</cn><cn>1</cn></interval> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
lowlimitとuplimitの組みも用いられます. この方法は, ひょっとしたら定積分で最も"標準的な"表現かもしれません.
The pair lowlimit and uplimit can also be used.
This is perhaps the most "standard" representation of this integral:
<apply><int/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>1</cn></uplimit> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
最終的に, ここに, 束縛変数に対してconditionを用いて表現した同じ定積分を示します.
Finally, here is the same integral, represented using
a condition on the bound variable:
<apply><int/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>x</ci></apply>
<apply><leq/><ci>x</ci><cn>1</cn></apply>
</apply>
</condition>
<apply><power/><ci>x</ci><cn>2</cn></apply>
</apply>conditionの式と一緒に明確な束縛変数を利用していることに注意して下さい. また, 束縛変数が用いられるとき, 非積分関数は, 関数の表記ではなく, 束縛変数の式の表記であることに注意して下さい.
Note the use of the explicit bound variable within the
condition term. Note also that when a bound
variable is used, the integrand is an expression in the bound
variable, not a function.
domainofapplicationと一緒にcondition要素を用いる一般的な手法はとても強力です. 例えば, 前に示した例を多変数の範囲に拡張するのに, 追加の束縛変数と, デカルト積に対応する関数の範囲を利用するかもしれません.
The general technique of using a condition element
together with domainofapplication is quite powerful. For
example, to extend the previous example to a multivariate domain, one
may use an extra bound variable and a domain of application
corresponding to a cartesian product:
<apply><int/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<domainofapplication>
<set>
<bvar><ci>t</ci></bvar>
<bvar><ci>u</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>t</ci></apply>
<apply><leq/><ci>t</ci><cn>1</cn></apply>
<apply><leq/><cn>0</cn><ci>u</ci></apply>
<apply><leq/><ci>u</ci><cn>1</cn></apply>
</apply>
</condition>
<list><ci>t</ci><ci>u</ci></list>
</set>
</domainofapplication>
<apply><times/>
<apply><power/><ci>x</ci><cn>2</cn></apply>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>
</apply>内側と外側の束縛変数の順番は意味があることに注意して下さい.
Note that the order of the inner and outer bound variables is significant.
厳格なコンテントMathMLへの対応付け
Mappings to Strict Content MathML
式を厳格なコンテントMathMLに書き換えるとき, 修飾要素はこの節で説明する一連の決まりによって取り除かれます. 修飾要素を含むMathMLの式を書き換えるための一般的なアルゴリズムは, 2段階で行われます. まず, interval, condition, uplimit, lowlimit修飾要素を使用している構造を, domainofapplicationのみを使用している構造に変換します. 続いて, domainofapplicationの式を厳格なコンテントマークアップに書き換えます.
When rewriting expressions to Strict Content MathML, qualifier
elements are removed via a series of rules described in this section.
The general algorithm for rewriting a MathML expression involving
qualifiers proceeds in two steps. First, constructs using the
interval, condition, uplimit and
lowlimit qualifiers are converted to constructs using only
domainofapplication. Second, domainofapplication
expressions are then rewritten as Strict Content markup.
書き換え: interval 修飾要素
Rewrite: interval qualifier
<apply> <bvar> </bvar> <lowlimit> </lowlimit> <uplimit> </uplimit> </apply>
<apply> <bvar> </bvar> <domainofapplication> <apply><csymbol cd="interval1"></csymbol> </apply> </domainofapplication> </apply>
この変換で使用される記号は, ここでは で表記している, 適用する関数の最初のものに依存します. 通常, 最初の式の意味が, より特定の区間の記号によって決められたり, そのような記号を示していたりする場合を除いて, intervalが使用されるべきです. 特に, 様々なコンテントMathML要素が, より特定の区間の記号と共に使用されるべきです. 最初の式がintの場合, oriented_intervalが用いられます. 最初の式が, sumまたはproductの場合, integer_intervalが使用されるべきです.
The symbol used in this translation depends on the head of the
application, denoted by
here. By default interval should be
used, unless the semantics of the head term can be determined and
indicate a more specific interval symbols. In particular, several
predefined Content MathML element should be used with more specific
interval symbols. If the head is int then oriented_interval is used. When the head term
is sum or product, integer_interval should be used.
lowlimitとuplimit修飾要素をdomainofapplication要素で置き換える上の手法は, interval修飾要素を置き換えるときにも用いらます.
The above technique for replacing lowlimit and uplimit qualifiers
with a domainofapplication element is also used for replacing the
interval qualifier.
condition修飾要素は, 大きな適用範囲でのブール値の式を指定することや, 与えられた値が制限された適用範囲の中かどうか指定することで, 束縛変数を制限します. condition要素は, 真値である条件を表す単独の子要素を含んでいます. 複雑な条件は, 条件の中で, andのようなブール値の演算子を適用することで形作ります.
The condition qualifier restricts a bound variable by specifying a
Boolean-valued expression on a larger domain, specifying whether a given value is in the
restricted domain. The condition element contains a single child that represents
the truth condition. Compound conditions are formed by applying Boolean operators such as
and in the condition.
書き換え: condition
Rewrite: condition
condition修飾要素を使用している式を, domainofapplicationを使用する式に書き換えるには次のようにします.
To rewrite an expression using the condition
qualifier as one using domainofapplication,
<bvar> </bvar> <bvar> </bvar> <condition> </condition>
この式は次のように書き換えられます.
is rewritten to
<bvar> </bvar> <bvar> </bvar> <domainofapplication> <apply><csymbol cd="set1">suchthat</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> <bvar> </bvar> </bind> </apply> </domainofapplication>
applyが, (ひょっとしたら元々はintervalまたはuplimit/lowlimitの組みとして表されていた)domainofapplicationを持っているとして, それらは を用いて表されます. 一方で は, 存在するなら第4.2.2.2節 <ci>の厳格でない利用で指定された, 束縛変数のtype属性によって決められる集合です. typeが指定されていない場合, 変換は, コンテント要素の識別子<ci>R</ci>として指定されている適用範囲を導入します.
If the apply has a domainofapplication (perhaps originally expressed as
interval or an uplimit/lowlimit pair) then that is used for
. Otherwise is a set determined by the type attribute
of the bound variable as specified in Section 4.2.2.2 Non-Strict uses of <ci>, if that is
present. If the type is unspecified, the translation introduces an unspecified domain via
content identifier <ci>R</ci>.
上の決まりを適用することで, interval, condition, uplimit, lowlimitを用いた式は, domainofapplicationのみを用いて書き換えられるでしょう. 一度domainofapplicationが得られたならば, 厳格なマークアップへの最終的な結び付けは, 次の決まりを用いて成し遂げられます.
By applying the rules above, expression using the
interval, condition, uplimit and
lowlimit can be rewritten using only
domainofapplication. Once a domainofapplication has
been obtained, the final mapping to Strict markup is accomplished
using the following rules:
書き換え: 制限
Rewrite: restriction
(束縛変数を伴わないapplyで表される)domainofapplication修飾要素によって修飾された関数の適用は, restriction記号によって構成される関数の適用の式に変換されます.
An application of a function that is qualified by the
domainofapplication qualifier (expressed by an apply element without
bound variables) is converted to an application of a function term constructed with the
restriction symbol.
<apply> <domainofapplication> </domainofapplication> </apply>
この式は次のように書き換えられるでしょう.
may be written as:
<apply>
<apply><csymbol cd="fns1">restriction</csymbol>
</apply>
</apply>一般に, 束縛変数や(おそらく)domainofapplicationを含む関数の適用は, 適用範囲を関数の最初に位置する引数とし, 変数の束縛をコード化するのにラムダ式を使用する, 次に示す決まりを用いて書き換えられます. この種類の演算子は, 後で説明する代わりの決まりが適用されます.
In general, an application involving bound variables and (possibly)
domainofapplication is rewritten using the following rule,
which makes the domain the first positional argument of the application,
and uses the lambda symbol to encode the variable bindings.
Certain classes of operator have alternative rules, as described below.
書き換え: apply bvar domainofapplication
Rewrite: apply bvar domainofapplication
束縛変数やdomainofapplicationを含むコンテントMathMLの式があるとします.
A content MathML expression with bound variables and
domainofapplication
<apply> <bvar> </bvar> ... <bvar> </bvar> <domainofapplication> </domainofapplication> ... </apply>
この式は次のように書き換えられます.
is rewritten to
<apply> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> ... <bvar> </bvar> </bind> ... <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> ... <bvar> </bvar> </bind> </apply>
1つもdomainofapplication修飾要素が無い時, 子要素 は省略されます.
If there is no domainofapplication qualifier the child is
omitted.
4.3.3.2 <degree>の利用
Uses of <degree>
| 種類 Class |
qualifier |
|---|---|
| 属性 Attributes |
CommonAtt |
| 内容 Content |
ContExp |
degree要素は, 演算の"次数"または"階数"を指定するのに使用される修飾要素です. MathMLは, degree要素を3つの文脈においてこの方法で使用します. 根号の次数や積率を指定するときや, 様々な微分係数の中でです. これらの各利用方法に対する特別な要素を導入する代わりに, MathMLは, 3つの状況全てに, 単独の一般的な構造degree要素を提供しています.
The degree element is a qualifier used to specify the
"degree" or "order" of an operation. MathML uses the
degree element in this way in three contexts: to specify the degree of a
root, a moment, and in various derivatives. Rather than introduce special elements for
each of these families, MathML provides a single general construct, the
degree element in all three cases.
degree修飾要素は, 前の方で議論した修飾要素と同じ意味合いで, 束縛変数を制限するのに使用しないことに注意して下さい. 実際に, 根号や積率と一緒に, 束縛変数が明確にも暗黙のうちにも何ら含まれることはありません. 微分の場合には, degree要素はbvarと結合されて用いられますが, この場合でさえ, 変数は純粋には束縛されていないでしょう.
Note that the degree qualifier is not used to restrict a bound variable in
the same sense of the qualifiers discussed above. Indeed, with roots and moments, no
bound variable is involved at all, either explicitly or implicitly. In the case of
differentiation, the degree element is used in conjunction with a
bvar, but even in these cases, the variable may not be genuinely bound.
rootやmoment演算子とのdegreeの利用については, 後で示すそれらの演算子の議論を参照して下さい. 微分でのdegreeの利用はより複雑です. 一般に, degree要素は, 変数に関する微分係数の階数を示します. degree要素は, 微分係数が適用される変数に対して変数を同一視するbvar要素の2番目の子要素として利用できます. ここに, degree修飾要素を使用した2階微分の例を示します.
For the usage of degree with the root and moment operators, see the discussion of those
operators below. The usage of degree in differentiation is more complex. In
general, the degree element indicates the order of the derivative with
respect to that variable. The degree element is allowed as the second child of a
bvar element identifying a variable with respect to which the derivative is
being taken. Here is an example of a second derivative using the degree
qualifier:
<apply><diff/>
<bvar>
<ci>x</ci>
<degree><cn>2</cn></degree>
</bvar>
<apply><power/><ci>x</ci><cn>4</cn></apply>
</apply>詳細については, 第4.4.4.2節 微分 <diff/>と第4.4.4.3節 偏微分 <partialdiff/>を参照して下さい.
For details see Section 4.4.4.2 Differentiation <diff/> and Section 4.4.4.3 Partial Differentiation <partialdiff/>.
4.3.3.3 <momentabout>と<logbase>の利用
Uses of <momentabout> and <logbase>
修飾要素momentaboutとlogbaseは, それぞれmomentやlog演算子と明確に一緒に利用される特別な要素です. それらの利用方法については, 後で示すそれらの演算子の説明を参照して下さい.
The qualifiers momentabout and logbase are
specialized elements specifically for use with the moment
and log operators
respectively. See the descriptions of those operators below for their usage.
4.3.4 演算子の種類
Operator Classes
次の節で詳細について説明されているコンテントMathML要素は, 大まかにいくつかの演算子の種類に分けられます. 各要素の演算子の種類は, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで要素を紹介している構文の表で示しています. その種類は, 要素の一般的に意図された数学的な利用方法を暗示したり, 構文によって決められる利用方法を決定したりもします. その種類によって, 厳格なコンテントMathMLに対応させるための, 適用可能な書き換えの決まりも決定されます. この節は, 演算子の種類に対する書き換えの決まりについて述べます.
The Content MathML elements described in detail in the next section may be broadly separated into classes. The class of each element is shown in the syntax table that introduces the element in Section 4.4 Content MathML for Specific Operators and Constants. The class gives an indication of the general intended mathematical usage of the element, and also determines its usage as determined by the schema. The class also determines the applicable rewrite rules for mapping to Strict Content MathML. This section presents the rewrite rules for each of the operator classes.
この節の決まりは, 具体的な演算子の種類に適用できる利用形態を網羅しています. 個々の要素に対する特別な場合の書き換えの決まりは, 後の節で議論しています. ただし, 最も一般的な利用方法の形態は典型的で, ほとんど全ての種類の演算子で利用されます. このことは, apply要素を用いて演算子を引数の明確な一覧に適用することで成り立ちます. それらの場合には, 厳格なコンテントMathMLに書き換えることは, 空要素を第4.4節 具体的な演算子と定数に対するコンテントMathMLの構文の表で一覧にした適切なcsymbolで置き換えることです. このことは, 次に示す決まりに要約されます.
The rules in this section cover the use cases applicable to
specific operator classes. Special-case rewrite rules for individual
elements are discussed in the sections below. However, the most
common usage pattern is generic, and is used by operators from almost all
operator classes. It consists of applying an operator to an explicit list
of arguments using an apply element. In these cases,
rewriting to Strict Content MathML is simply a matter of replacing the
empty element with an appropriate csymbol, as listed in the
syntax tables in Section 4.4 Content MathML for Specific Operators and Constants. This is summarized in
the following rule.
書き換え: 要素
Rewrite: element
例えば, 次の式があるとします.
For example,
この式は, 次の厳格な形式と等価です.
is equivalent to the Strict form
<csymbol cd=""></csymbol>
MathML2では, definitionURL属性が, 演算子要素の意味を再定義または修正するのに使われていたでしょう. definitionURL属性が存在する場合, csymbolのcd属性の値は, 可能な限りdefinitionURLの値によって決定されるべきです. cdの値とdefinitionURLの値の間の対応は, 第4.2.3.2節 <csymbol>の厳格でない利用で説明しています.
In MathML 2, the definitionURL attribute could be
used to redefine or modify the meaning of an operator element. When the definitionURL
attribute is present, the value for the cd attribute on the csymbol should be
determined by the definitionURL value if possible. The correspondence between cd and definitionURL values is described Section 4.2.3.2 Non-Strict uses of <csymbol>.
4.3.4.1 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)
N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor)
たくさんのMathML演算子は, 任意の数の引数と一緒に利用されるかもしれません. それらの種類の要素に対応するOpenMath記号も, 任意の数の引数を必要とします. 全てのそのような場合に, applyまたはbind要素の子要素として, 引数が明確に示されるか, もしくは, 修飾要素の利用を通じて, 一覧が暗に指定されるかするでしょう.
Many MathML operators may be used with an arbitrary number of
arguments. The corresponding OpenMath symbols for elements in these classes
also take an arbitrary number of arguments.
In all such cases, either the arguments my be given
explicitly as children of the apply or bind element, or
the list may be specified implicitly via the use of qualifier
elements.
4.3.4.1.1 構文形式
Schema Patterns
複数項の演算子を表す要素は, 付録A MathMLの処理のnary-arith.class, nary-functional.class, nary-logical.class, nary-linalg.class, nary-set.class, nary-constructor.classといった構文形式で指定されます.
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-arith.class, nary-functional.class, nary-logical.class, nary-linalg.class, nary-set.class, nary-constructor.class.
4.3.4.1.2 厳格なコンテントMathMLへの書き換え
Rewriting to Strict Content MathML
引数の一覧が明確に示されるならば, 書き換え: 要素の決まりが適用されます.
If the argument list is given explicitly, the Rewrite: element rule applies.
どの修飾要素の利用も, 次の決まりで示したapply_to_list記号を用いて, 引数の一覧に関数をはっきりと適用することによって, 厳格なコンテントMathMLで表されます. 前に説明したようにdomainofapplication以外の修飾要素はdomainofapplicationに書き換えられることから, この決まりは, domainofapplication修飾要素のみを考慮しています.
Any use of qualifier elements is expressed in Strict Content
MathML, via explicitly applying the function to a list of arguments
using the apply_to_list symbol as shown
in the following rule. The rule only considers the
domainofapplication qualifier as other qualifiers may be
rewritten to domainofapplication as described earlier.
書き換え: 複数項の演算子 domainofapplication
Rewrite: n-ary domainofapplication
次に示す形式の式で, は, 関数の種類を表す何らかの要素で, は, 束縛変数を含む任意の式です.
An expression of the following form,
where represents any
element of the relevant class and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
この式は, 次のように書き換えられます.
is rewritten to
<apply><csymbol cd="fns2">apply_to_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
上の決まりは, 一覧にされた演算子の種類の全ての記号に適用されます. nary-set.classの場合, 使用されるコンテント辞書の選択は, 引数のtype属性に依存し, 通常はset1が, type="multiset"の場合はmultiset1が使用されるべきです.
The above rule applies to all symbols in the listed classes.
In the case of nary-set.class the choice of Content
Dictionary to use depends on the type attribute on the
arguments, defaulting to set1, but multiset1
should be used if type="multiset".
vectorといった, nary-constructor.classの中の要素は, 引数と修飾要素を, 囲っているapplyの子要素ではなく, その要素自身の子要素として示す構築要素の構文を使用することに注意して下さい. この場合, 上の決まりは, 類似した構文上の修飾と一緒に適用されます.
Note that the members of the nary-constructor.class, such
as vector, use constructor syntax where the arguments and
qualifiers are given as children of the element rather than as
children of a containing apply. In this case, the above rules apply
with the analogous syntactic modifications.
4.3.4.2 集合やリストに対する複数項の演算子(種類nary-setlist-constructor)
N-ary Constructors for set and list (class nary-setlist-constructor)
setとlistの利用は, 他の複数項の構築要素と同じ形式に従いますが, 厳格なコンテントMathMLに書き換えるとき, 前に示した決まりとは異なるものが用いられます. これは, map記号が暗に, 必要とされる集合やリストを構築しているためで, apply_to_listは, この場合に必要ありません.
The use of set and list follows the same format
as other n-ary constructors, however when rewriting to Strict
Content MathML a variant of the above rule is used. This is because the map
symbol implicitly constructs the required set or list, and apply_to_list is
not needed in this case.
4.3.4.2.1 構文形式
Schema Patterns
これらの複数項の演算子を表している要素は, nary-setlist-constructor.class構文形式で指定されます.
The elements representing these n-ary operators are specified in the schema pattern nary-setlist-constructor.class.
4.3.4.2.2 厳格なコンテントMathMLへの書き換え
Rewriting to Strict Content MathML
引数の一覧が明確に示されるならば, 書き換え: 要素の決まりが適用されます.
If the argument list is given explicitly, the Rewrite: element rule applies.
修飾要素が, 引数の一覧を指定するために利用される場合, 次の決まりが用いられます.
When qualifiers are used to specify the list of arguments, the following rule is used.
書き換え: 複数項の集合やリスト domainofapplication
Rewrite: n-ary setlist domainofapplication
次に示す形式の式で, は, 要素setまたはlistのどちらかで, は, 束縛変数を含む任意の式です.
An expression of the following form,
where is either of the elements set or list and
is an arbitrary expression involving the bound variable(s)
<bvar> </bvar> <domainofapplication> </domainofapplication>
この式は, 次のように書き換えられます.
is rewritten to
<apply><csymbol cd="">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
が既に入れ物要素に対する適切な型の集合またはリストであり, から創られたラムダ式が同一であるとき, 全ての入れ物要素は, 直接 として書き換えられるべきことに注意して下さい.
Note that
when is already a set
or list of the appropriate type for the container element, and the lambda function created
from is
the identity, the entire container element should be rewritten
directly as .
setの場合, コンテント辞書と記号の選択は, 引数のtype属性の値に依存します. 通常, set記号が用いられますが, 引数のどれかが"multiset"の値であるtype属性を持つならば, multiset記号が用いられます. "set"でも"multiset"でもない値のtype属性がある場合, set記号が使われるべきで, 引数は, 書き換え: 属性の決まりを使ってそれら自身のtype属性を書き換えた型が付加されるべきです.
In the case of set, the choice of Content
Dictionary and symbol depends on the value of the type attribute of the arguments. By default the set symbol is used, but if one of the arguments has
type attribute with value "multiset", the multiset symbol is used.
If there is a type attribute with value other than "set" or "multiset"
the set symbol should be used, and the arguments should be annotated with their type
by rewriting the type attribute using the rule
Rewrite: attributes.
4.3.4.3 複数項の関係演算子(種類nary-reln, nary-set-reln)
N-ary Relations (classes nary-reln, nary-set-reln)
MathMLは, a < b < c < dといった関係の"連鎖"に自然な式を与えるため, 複数の引数と一緒に利用される推移的な関係演算子を認めています. ただし, 算術演算子の場合と異なり, 厳格なコンテントMathMLで使われる基本となる記号は, 二項演算子に分類されます. そのため, 前の節で示したapply_to_listを利用することは不可能ですが, 代わりに類似した関数predicate_on_listが使用され, その意味は本来, 同時に2つの範囲の要素に述語を適用して結合することです.
MathML allows transitive relations to be used with multiple arguments, to give a natural expression to "chains" of relations such as a < b < c < d. However unlike the case of the arithmetic operators, the underlying symbols used in the Strict Content MathML are classed as binary, so it is not possible to use apply_to_list as in the previous section, but instead a similar function predicate_on_list is used, the semantics of which is essentially to take the conjunction of applying the predicate to elements of the domain two at a time.
4.3.4.3.1 構文形式
Schema Patterns
これらの複数項の演算子を表す要素は, 付録A MathMLの処理のnary-reln.class, nary-set-reln.classといった構文形式で指定されます.
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-reln.class, nary-set-reln.class.
4.3.4.3.2 厳格なコンテントMathMLへの書き換え
Rewriting to Strict Content MathML
書き換え: 複数項の関係演算子
Rewrite: n-ary relations
次の形式の式があるとします.
An expression of the form
<apply> </apply>
この式は, 次の厳格なコンテントMathMLに書き換えられます.
rewrites to Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">list</csymbol> </apply> </apply>
書き換え: 複数項の関係演算子 bvar
Rewrite: n-ary relations bvar
次の形式の式があるとします.
An expression of the form
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
が束縛変数を含む任意の式であるならば, この式は, 次の厳格なコンテントMathMLに書き換えられます.
where
is an arbitrary expression involving the bound variable, rewrites to the Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd=""></csymbol> <apply><csymbol cd="list1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
上の決まりは, 種類nary-reln.classとnary-set-reln.classの全ての記号に適用されます. 後者の場合には, 用いられるコンテント辞書の選択は, 記号のtype属性に依存し, 通常はset1が, type="multiset"の場合はmultiset1が使用されるべきです.
The above rules apply to all symbols in classes nary-reln.class
and nary-set-reln.class. In the latter case the choice of Content
Dictionary to use depends on the type attribute on the
symbol, defaulting to set1, but multiset1
should be used if type="multiset".
4.3.4.4 複数項または単一項の演算子(種類nary-minmax, nary-stats)
N-ary/Unary Operators (classes nary-minmax, nary-stats)
MathML要素max, min, およびmeanといった統計要素の中には, 前に示した種類の複数項の関数として使われるものもあるでしょう. しかしながら, 単独の引数が提供されている場合には, 特別な解釈が行われます. 単独の引数が提供された場合, 関数が引数によって表された要素に適用されます.
The MathML elements, max, min and some statistical
elements such as mean may be used as a n-ary function as in
the above classes, however a special interpretation is given in the
case that a single argument is supplied. If a single argument is
supplied the function is applied to the elements represented by the
argument.
これらの要素に対して厳格なコンテントMathMLで用いられる, 基本となる記号は単一項の演算子です. そのため, 0個もしくは複数の引数と一緒にMathMLが利用される場合, 関数は, 次に示す決まりによって明確に提供された引数から構築される集合に適用されます.
The underlying symbol used in Strict Content MathML for these elements is Unary and so if the MathML is used with 0 or more than 1 arguments, the function is applied to the set constructed from the explicitly supplied arguments according to the following rule.
4.3.4.4.1 構文形式
Schema Patterns
これらの複数項の演算子を表す要素は, 付録A MathMLの処理のnary-minmax.class, nary-stats.classといった構文形式で指定されます.
The elements representing these n-ary operators are specified in the following schema patterns in Appendix A Parsing MathML: nary-minmax.class, nary-stats.class.
4.3.4.4.2 厳格なコンテントMathMLへの書き換え
Rewriting to Strict Content MathML
書き換え: 複数項または単一項の演算子 集合
Rewrite: n-ary unary set
演算子の種類nary-statsまたはnary-minmaxの要素が, 0個, または2個, またはさらに多くの引数の明確な一覧 に適用される場合を考えます.
When an element,
, of class nary-stats or nary-minmax
is applied to an explicit
list of 0 or 2 or more arguments,
<apply> </apply>
この式は, <csymbol cd="set1" name="set"/>記号を用いて構築される引数の集合に対する, 要素の構文の表で指定された記号<csymbol cd="" name=""/>の単一項の関数の適用に変換されます.
It is is translated to the unary application of the symbol
<csymbol cd="" name=""/>
as specified in the syntax table for the element to the set of
arguments, constructed using the
<csymbol cd="set1" name="set"/>
symbol.
<apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">set</csymbol> </apply> </apply>
全てのMathMLの複数項の演算子のように, 引数の一覧は, 暗に修飾要素を用いて指定されるかもしれません. このことは, 次に示す決まりを用いて厳格なコンテントMathMLで表されます. その決まりは, 書き換え: 複数項の演算子 domainofapplicationの決まりに似ていますが, 引数で構築された集合に記号が直接適用される点で異なっており, apply_to_listを使用する必要がありません.
Like all MathML n-ary operators, The list of arguments may be specified implicitly using qualifier elements. This is expressed in Strict Content MathML using the following rule, which is similar to the rule Rewrite: n-ary domainofapplication but differs in that the symbol can be directly applied to the constructed set of arguments and it is not necessary to use apply_to_list.
書き換え: 複数項または単一項の演算子 domainofapplication
Rewrite: n-ary unary domainofapplication
次の形式の式があり, が何らかの関係演算子の種類の要素を表しており, は束縛変数を含む任意の式です.
An expression of the following form,
where represents any
element of the relevant class and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
この式は, 次のように書き換えられます.
is rewritten to
<apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">map</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply> </apply>
が明確に集合で, から構築されるラムダ式がいつも同じならば, domainofapplicationの項は, で直接書き換えられるべきことに注意して下さい.
Note that
when is already a set
and the lambda function created from is
the identity, the domainofapplication term should should be
rewritten directly
as .
要素が単独の引数に適用される場合, set記号は使われず, 要素に対する記号が直接引数に適用されます.
If the element is applied to a single argument the set symbol is not used and the symbol is applied directly to the argument.
書き換え: 複数項または単一項の演算子 単独の引数
Rewrite: n-ary unary single
種類nary-statsまたはnary-minmaxの要素が単独の引数に適用されるとします.
When an element,
, of class nary-stats or nary-minmax
is applied to a single argument,
<apply> </apply>
この式は, 要素の構文の表に基づいて, 単一項の記号の適用に変換されます.
It is is translated to the unary application of the symbol in the syntax table for the element.
<apply><csymbol cd=""></csymbol> </apply>
注意: MathMLの初期のバージョンは, この種類の要素の正確な解釈をはっきりさせておらず, max(X)といった式が, 単集合に対する最大関数の適用なのか, もしくは集合Xの最大値を意味するものと解釈されるべきか, 定義しないままにしていました. 書き換え: 複数項または単一項の演算子 単独の引数の決まりを, 提供された引数がスカラーなので適用できないと判断したソフトウェアは, エラーの回復のために書き換え: 複数項または単一項の演算子 集合の決まりを使おうとするかもしれません. より困難なことに, 統計関数の場合に用いられるコンテント辞書は, 明確なデータの集合または分布を表す確立変数としての, 引数の望まれた解釈に依存します.
Note: Earlier versions of MathML were not explicit about the correct interpretation of elements in this class, and left it undefined as to whether an expression such as max(X) was a trivial application of max to a singleton, or whether it should be interpreted as meaning the maximum of values of the set X. Applications finding that the rule Rewrite: n-ary unary single can not be applied as the supplied argument is a scalar may wish to use the rule Rewrite: n-ary unary set as an error recovery. As a further complication, in the case of the statistical functions the Content Dictionary to use in this case depends on the desired interpretation of the argument as a set of explicit data or a random variable representing a distribution.
4.3.4.5 二項演算子(種類 binary-arith, binary-logical, binary-reln, binary-linalg, binary-set)
Binary Operators (classes binary-arith, binary-logical, binary-reln, binary-linalg, binary-set)
二項演算子は2つの引数を伴い, 何らかの特別な書き換えの決まりを必要とせずに, 単純に書き換え: 要素の決まりによってOpenMath記号と結び付けられます. 二項の構築要素intervalは類似していますが, 引数が要素の子要素となる構築要素の構文を使用しており, 使用される記号は, Section 4.4.1.1 範囲 <interval>で述べられているtype属性に依存します.
Binary operators take two arguments and simply map to OpenMath
symbols via Rewrite: element
without the need of any special rewrite rules. The binary
constructor interval is similar but uses constructor syntax
in which the arguments are children of the element, and the symbol
used depends on the type element as described in Section 4.4.1.1 Interval <interval>
4.3.4.5.1 構文形式
Schema Patterns
これらの二項演算子を表す要素は, 付録A MathMLの処理のbinary-arith.class, binary-logical.class, binary-reln.class, binary-linalg.class, binary-set.classといった構文形式で指定されます.
The elements representing these binary operators are specified in the following schema patterns in Appendix A Parsing MathML: binary-arith.class, binary-logical.class, binary-reln.class, binary-linalg.class, binary-set.class.
4.3.4.6 単一項の演算子(種類unary-arith, unary-linalg, unary-functional, unary-set, unary-elementary, unary-veccalc)
Unary Operators (classes unary-arith, unary-linalg, unary-functional, unary-set, unary-elementary, unary-veccalc)
単一項の演算子は単独の引数を必要とし, 何らかの特別な書き換えの決まりを必要とせずに, 書き換え: 要素の決まりによってOpenMath記号と結び付けられます.
Unary operators take a single argument and map to OpenMath symbols via Rewrite: element without the need of any special rewrite rules.
4.3.4.6.1 構文形式
Schema Patterns
これらの単一項の演算子を表す要素は, 付録A MathMLの処理のunary-arith.class, unary-functional.class, unary-set.class, unary-elementary.class, unary-veccalc.classといった構文形式で指定されます.
The elements representing these unary operators are specified in the following schema patterns in Appendix A Parsing MathML: unary-arith.class, unary-functional.class, unary-set.class, unary-elementary.class, unary-veccalc.class.
4.3.4.7 定数(種類constant-arith, constant-set)
Constants (classes constant-arith, constant-set)
定数記号は, eや真値といった数学定数, また, 実数や整数といった集合の名前に関係します. 厳格なコンテントMathMLでは, それらは, 単純に第4.4.10節 定数要素と記号要素のそれらの要素の構文の表で一覧にした対応する記号に書き換えられます.
Constant symbols relate to mathematical constants such as e and true and also to names of sets such as the Real Numbers, and Integers. In Strict Content MathML, they rewrite simply to the corresponding symbol listed in the syntax tables for these elements in Section 4.4.10 Constant and Symbol Elements.
4.3.4.7.1 構文形式
Schema Patterns
それらの定数を表す要素は, constant-arith.classとconstant-set.classの構文形式で指定されます.
The elements representing these constants are specified in the schema patterns constant-arith.class and constant-set.class.
4.3.4.8 量化記号(種類quantifier)
Quantifiers (class quantifier)
量化記号という演算子の種類は, 述語計算の全称記号と存在記号に使われます.
The Quantifier class is used for the forall and exists quantifiers of predicate calculus.
4.3.4.8.1 構文形式
Schema Patterns
量化記号を表す要素は, quantifier.class構造形式で指定されます.
The elements representing quantifiers are specified in the schema pattern quantifier.class.
4.3.4.8.2 厳格なコンテントMathMLへの書き換え
Rewriting to Strict Content MathML
bindと修飾要素無しで用いられる場合, 厳格なコンテントMathMLでの解釈は単純です. 一般に, applyまたは修飾要素と用いられる場合, 厳格なコンテントMathMLでの解釈は, 次の決まりを通して行われます.
If used with bind and no qualifiers,
then the interpretation in Strict Content MathML is simple. In general
if used with apply or qualifiers, the interpretation in
Strict Content MathML is via the following rule.
書き換え: 量化記号
Rewrite: quantifier
次の形式の式があり, が量化記号という演算子の種類の要素を示しており, は束縛変数を含む任意の式です.
An expression of following form where
denotes an element of
class quantifier and
is an arbitrary expression involving the bound variable(s)
<apply> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
この式は, 次のように書き換えられます.
is rewritten to an expression
<bind><csymbol cd=""></csymbol> <bvar> </bvar> <apply><csymbol cd=""></csymbol> <apply><csymbol cd="set1">in</csymbol> </apply> </apply> </bind>
ここで, 記号<csymbol cd=""></csymbol>と<csymbol cd=""></csymbol>は, 要素の構文の式で指定されたものです. (existsの場合にand, forallの場合にimpliesとなる追加の記号が必要です.) domainofapplicationが1つも存在しないならば, 論理的な結合は必要なく, 直接変換されます.
where the symbols
<csymbol cd=""></csymbol>
and
<csymbol cd=""></csymbol>
are as specified in the syntax table of the element.
(The additional symbol being
and in the case of exists and
implies in the case of forall.) When no
domainofapplication is present, no logical conjunction is necessary, and the translation
is direct.
4.3.4.9 他の演算子(種類lambda, interval, int, diff partialdiff, sum, product, limit)
Other Operators (classes lambda, interval, int, diff partialdiff, sum, product, limit)
特別な目的を持った演算子の種類が, 適切な要素に対する節で説明されています.
Special purpose classes, described in the sections for the appropriate elements
4.3.4.9.1 構文形式
Schema Patterns
この要素は, 付録A MathMLの処理のlambda.class, interval.class, int.class, partialdiff.class, sum.class, product.class, limit.classの構文形式で指定されます.
The elements are specified in the following schema patterns in Appendix A Parsing MathML: lambda.class, interval.class, int.class, partialdiff.class, sum.class, product.class, limit.class.
4.3.5 厳格でない属性
Non-strict Attributes
cnやintervalといった数々のコンテントMathMLの要素が, それらが表す事象の意味を専門に扱う属性を認めています. これらの場合に, 特別な書き換えの決まりが, 第4.4節 具体的な演算子と定数に対するコンテントMathMLでの, 基本となる状況に応じて与えられます. ただし, コンテントMathML要素はまた, 全てのMathML要素で利用される属性を受入れ, 文脈に応じて他の名前空間の属性を含むかもしれません. このような属性は, 厳格なコンテントマークアップの, 代わりの形式に書き換えられなければなりません.
A number of content MathML elements such as cn and
interval allow attributes to specialize the semantics of the
objects they represent. For these cases, special rewrite rules are
given on a case-by-case basis in Section 4.4 Content MathML for Specific Operators and Constants. However,
content MathML elements also accept attributes shared all MathML elements, and
depending on the context, may also contain attributes from other XML
namespaces. Such attributes must be rewritten in alternative form in
Strict Content Markup.
書き換え: 属性
Rewrite: attributes
例えば, 次の式があるとします.
For instance,
<ci class="" xmlns:other="" other:att=""></ci>
この式は次のように書き換えられます.
is rewritten to
<semantics> <ci></ci> <annotation cd="mathmlattr" name="class" encoding="text/plain"></annotation> <annotation-xml cd="mathmlattr" name="foreign" encoding="MathML-Content"> <apply><csymbol cd="mathmlattr">foreign_attribute</csymbol> <cs></cs> <cs></cs> <cs></cs> <cs></cs> </apply> </annotation-xml> </semantics>
厳格なコンテントMathMLで認められていないMathML属性に対し, コンテント辞書mathmlattrが参照されます. このコンテント辞書は, コンテントMathML要素で認められている全ての属性に対する記号を提供します.
For MathML attributes not allowed in Strict Content MathML the content dictionary mathmlattr is referenced, which provides symbols for all attributes allowed on content MathML elements.
4.4 具体的な演算子と定数に対するコンテントMathML
Content MathML for Specific Operators and Constants
この節は, 数学演算子, 関数, 定数の中心となる集合を表す要素を紹介します. ほとんどは空要素で, 微積分の段階までの標準的な数学の課程の事象を網羅しています. 残りの要素は, 集合, 範囲, ベクトルなどに対する入れ物要素です. 簡潔であるように, この節で定義する全ての要素は, ときどき演算子要素と呼ばれます.
This section presents elements representing a core set of mathematical operators, functions and constants. Most are empty elements, covering the subject matter of standard mathematics curricula up to the level of calculus. The remaining elements are container elements for sets, intervals, vectors and so on. For brevity, all elements defined in this section are sometimes called operator elements.
後の各小節は, 具体的な演算子要素について議論しており, その要素の演算子の種類を示す構文の表から始まります. 厳格なマークアップに書き換える特別な場合の決まりは, 必要に応じて紹介しています. ただし, ほとんどの場合に, 適切な演算子の種類に対する一般的な書き換えの決まりで十分です. 特に, 他の方法が示されていない限り, 要素は, 通常の書き換え: 要素の決まりを用いて書き換えられます. ただし, この節の全ての要素は, 厳格なコンテントマークアップで認められていないことから, 何らかの形式に書き換えられなければならないことに注意して下さい.
Each subsection below discusses a specific operator element, beginning with a syntax table, giving the elements operator class. Special case rules for rewriting as Strict Markup are introduced as needed. However, in most cases, the generic rewrite rules for the appropriate operator class is sufficient. In particular, unless otherwise indicated, elements are to be rewritten using the default Rewrite: element rule. Note, however, that all elements in this section must be rewritten in some fashion, since they are not allowed in Strict Content markup.
MathML2では, definitionURL属性は, 演算子要素の意味を再定義したり, 修正したりするのに用いられることができました. definitionURL属性のこの利用方法は, MathML3では非推奨です. 代わりに, csymbol要素が用いられるべきです. 一般に, csymbolのcd属性の値は, definitionURLの値に一致するでしょう.
In MathML 2, the definitionURL attribute could be
used to redefine or modify the meaning of an operator
element. This use of the definitionURL attribute is deprecated in MathML 3. Instead a
csymbol element should be used. In general, the value of
cd attribute on the csymbol will correspond to
the definitionURL value.
4.4.1 関数と逆関数
Functions and Inverses
4.4.1.1 範囲 <interval>
Interval <interval>
| 種類 Class |
interval |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt,closure? |
| 内容 Content |
ContExp,ContExp |
| OM記号 OM Symbols |
interval_cc, interval_oc, interval_co, interval_oo |
interval要素は, 実数の数直線の単純な範囲を表すのに用いられる入れ物要素です. この要素は, 既定値が"closed"の必須でない属性closureを伴います.
The interval element is a container element used to represent simple mathematical intervals of the
real number line. It takes an optional attribute closure, with a default value
of "closed".
コンテントMathML
Content MathML
<interval closure="open"><ci>x</ci><cn>1</cn></interval>
<interval closure="closed"><cn>0</cn><cn>1</cn></interval>
<interval closure="open-closed"><cn>0</cn><cn>1</cn></interval>
<interval closure="closed-open"><cn>0</cn><cn>1</cn></interval>
表示例
Sample Presentation
<mfenced><mi>x</mi><mn>1</mn></mfenced>
<mfenced open="[" close="]"><mn>0</mn><mn>1</mn></mfenced>
<mfenced open="(" close="]"><mn>0</mn><mn>1</mn></mfenced><mfenced open="[" close=")"><mn>0</mn><mn>1</mn></mfenced>
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
厳格なマークアップでは, interval要素は, interval1コンテント辞書の4つの記号の1つに対応付けられます. closureの値が"open"であれば, intervalはinterval_ooに対応付けられます. 値が"closed"ならintervalは記号interval_ccに, 値が"open-closed"ならinterval_ocに, 値が"closed-open" ならinterval_coに対応付けられます.
In Strict markup, the interval element corresponds to one
of four symbols from the interval1 content
dictionary. If closure has the value "open" then
interval corresponds to the
interval_oo.
With the value "closed"
interval corresponds to the symbol
interval_cc,
with value "open-closed" to
interval_oc, and with
"closed-open" to
interval_co.
4.4.1.2 逆関数 <inverse>
Inverse <inverse>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
inverse |
inverse要素は, 関数の機能的に逆となる一般的な式を構築するために, その関数に適用されます. inverse要素は, 引数に適用されるか, または単独で現れるかします. 単独で現れる場合, その要素は他の関数で結果的に反対のふるまいをする演算子を表します.
The inverse element is applied to a function in order to
construct a generic expression for the functional inverse of that
function. The inverse element may either be applied to
arguments, or it may appear alone, in which case it represents an
abstract inversion operator acting on other functions.
コンテントMathML
Content MathML
<apply><inverse/> <ci> f </ci> </apply>
表示例
Sample Presentation
<msup><mi>f</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup>
コンテントMathML
Content MathML
<apply> <apply><inverse/><ci type="matrix">A</ci></apply> <ci>a</ci> </apply>
表示例
Sample Presentation
<mrow> <msup><mi>A</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>a</mi></mfenced> </mrow>
4.4.1.3 ラムダ式 <lambda>
Lambda <lambda>
| 種類 Class |
lambda |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
BvarQ, DomainQ, ContExp |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
lambda |
lambda要素は, 式, 束縛変数, 修飾要素から利用者が定義した関数を構築するのに使われます. (0個でも良い)n個の束縛変数から構築されるラムダ式において, 最初のn個の子要素はbvar要素で, 実際の関数の値に相当する最後の子要素で, 仮引数として使われる変数を指定します. 束縛変数は, 必須でないdomainofapplication修飾要素か, その簡潔な表記によって制限できます. lambda構造の意味するところは, 束縛変数で各引数を置き換えた, 最後の子要素の中の式を返す複数項の演算子です.
The lambda element is used to construct a user-defined
function from an expression, bound variables, and qualifiers. In a
lambda construct with n (possibly 0) bound variables, the
first n children are bvar elements that identify
the variables that are used as placeholders in the last child for
actual parameter values. The bound variables can be restricted by an
optional domainofapplication qualifier or one of its
shorthand
notations. The meaning of the lambda construct is an
n-ary function that returns the expression in the last
child where the bound variables are replaced with the respective
arguments.
domainofapplication子要素は, 構築された関数の結果の取り得る値を制限します. 実際のところ, 次のlambda構造は, 整数の関数を表しています.
The domainofapplication child restricts the possible
values of the arguments of the constructed function. For instance, the
following lambda construct represents a function on
the integers.
<lambda> <bvar><ci> x </ci></bvar> <domainofapplication><integers/></domainofapplication> <apply><sin/><ci> x </ci></apply> </lambda>
lambda構造が束縛変数を含んでいない場合, そのlambda構造は, domainofapplication構造を含んでいない限り必要なく, 取り除かれるかもしれません. そのような場合, lambda構造の最後の子要素は, それ自身が関数で, 上の関数の別の表現である次の例のように, domainofapplicationがその機能的な式を制限します.
If a lambda construct does not contain bound variables, then
the lambda construct is superfluous and may be removed,
unless it also contains a domainofapplication construct.
In that case, if the last child of the lambda construct is
itself a function, then the domainofapplication restricts
its existing functional arguments, as in this example, which is
a variant representation for the function above.
<lambda> <domainofapplication><integers/></domainofapplication> <sin/> </lambda>
そうでない場合, lambda構造の最後の子要素は, 関数ではなく数字と見なされ, lambda構造は関数ではなく, 同じ数字で, どのdomainofapplicationも無視されます.
Otherwise, if the last child of the lambda construct is not a
function, say a number, then the lambda construct will not be
a function, but the same number, and any domainofapplication
is ignored.
コンテントMathML
Content MathML
<lambda>
<bvar><ci>x</ci></bvar>
<apply><sin/>
<apply><plus/><ci>x</ci><cn>1</cn></apply>
</apply>
</lambda>表示例
Sample Presentation
<mrow> <mi>λ<!--GREEK SMALL LETTER LAMDA--></mi> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mi>sin</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mrow><mo>(</mo><mi>x</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow> </mrow> </mfenced> </mrow>
<mrow> <mi>x</mi> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow> <mi>sin</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mrow><mo>(</mo><mi>x</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow> </mrow> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
書き換え: lambda
Rewrite: lambda
lambda要素が修飾要素を含んでいない場合, ラムダ式は, 直接bindの式に変換されます.
If the lambda element does not contain qualifiers, the
lambda expression is directly translated into a bind
expression.
<lambda> <bvar> </bvar><bvar> </bvar> </lambda>
この式は, 次の厳格なコンテントMathMLに書き換えられます.
rewrites to the Strict Content MathML
<bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar><bvar> </bvar> </bind>
書き換え: lambda domainofapplication
Rewrite: lambda domainofapplication
lambda要素が修飾要素を含んでいて, 修飾要素がdomainofapplicationに書き換えられる場合, ラムダ式は, lambdaで構成される関数の式に変換され, restrictionを用いて指定された範囲に制限されます.
If the lambda element does contain qualifiers, the
qualifier may be rewritten to domainofapplication
and then the lambda expression is translated to a
function term constructed with lambda
and restricted to the specified domain using
restriction.
<lambda> <bvar> </bvar><bvar> </bvar> <domainofapplication> </domainofapplication> </lambda>
この式は, 次の厳格なコンテントMathMLに書き換えられます.
rewrites to the Strict Content MathML
<apply><csymbol cd="fns1">restriction</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar><bvar> </bvar>
</bind>
</apply>4.4.1.4 関数の合成 <compose/>
Function composition <compose/>
| 種類 Class |
nary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
left_compose |
compose要素は, 関数の合成の演算子を表します. MathMLは, 合成される関数の定義域や値域について, 何も想定していないことに注意して下さい. 合成された関数の定義域は空集合かもしれません.
The compose element represents the function
composition operator. Note that MathML makes no assumption about the domain
and codomain of the constituent functions in a composition; the domain of the
resulting composition may be empty.
compose要素は, 交換法則を満たす複数項の演算子です. 結果として, この演算子は, 第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で説明されている修飾要素を用いて, (場合によっては無限の)集合が並んだ式の一覧で定義された, 合成された演算子に引き上げられるかもしれません.
The compose element is a commutative n-ary operator. Consequently, it may be
lifted to the induced operator defined on a collection of arguments indexed by a (possibly
infinite) set by using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
コンテントMathML
Content MathML
<apply><compose/><ci>f</ci><ci>g</ci><ci>h</ci></apply>
表示例
Sample Presentation
<mrow><mi>f</mi><mo>∘<!--RING OPERATOR--></mo><mi>g</mi><mo>∘<!--RING OPERATOR--></mo><mi>h</mi></mrow>
コンテントMathML
Content MathML
<apply><eq/>
<apply>
<apply><compose/><ci>f</ci><ci>g</ci></apply>
<ci>x</ci>
</apply>
<apply><ci>f</ci><apply><ci>g</ci><ci>x</ci></apply></apply>
</apply>表示例
Sample Presentation
<mrow> <mrow> <mrow><mo>(</mo><mi>f</mi><mo>∘<!--RING OPERATOR--></mo><mi>g</mi><mo>)</mo></mrow> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>x</mi></mfenced> </mrow> <mo>=</mo> <mrow> <mi>f</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced> <mrow> <mi>g</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>x</mi></mfenced> </mrow> </mfenced> </mrow> </mrow>
4.4.1.5 恒等関数 <ident/>
Identity function <ident/>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
identity |
ident要素は, 恒等関数を表します. MathMLは, 表現された恒等関数の定義域や値域について何も想定していないことに注意して下さい. それらは, 関数が使われた文脈に依存します.
The ident element represents the
identity function. Note that MathML makes no assumption about the
domain and codomain of the represented identity function, which
depends on the context in which it is used.
コンテントMathML
Content MathML
<apply><eq/>
<apply><compose/>
<ci type="function">f</ci>
<apply><inverse/>
<ci type="function">f</ci>
</apply>
</apply>
<ident/>
</apply>表示例
Sample Presentation
<mrow> <mrow> <mi>f</mi> <mo>∘<!--RING OPERATOR--></mo> <msup><mi>f</mi><mrow><mo>(</mo><mn>-1</mn><mo>)</mo></mrow></msup> </mrow> <mo>=</mo> <mi>id</mi> </mrow>
4.4.1.6 定義域 <domain/>
Domain <domain/>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
domain |
domain要素は, この要素が適用される関数の定義域を表します. 定義域は, 関数が定義されているところの値の集合です.
The domain element represents the domain of the
function to which it is applied. The domain is the set of values
over which the function is defined.
コンテントMathML
Content MathML
<apply><eq/> <apply><domain/><ci>f</ci></apply> <reals/> </apply>
表示例
Sample Presentation
<mrow> <mrow><mi>domain</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>f</mi></mfenced></mrow> <mo>=</mo> <mi mathvariant="double-struck">R</mi> </mrow>
4.4.1.7 値域 <codomain/>
codomain <codomain/>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
range |
codomain要素は, この要素が適用される関数の終域または値域を表します. 終域は, 関数の像と等しい必要は無く, 単に像を含む必要があるだけです.
The codomain represents the codomain, or range, of the function
to which is is applied. Note that the codomain is not necessarily
equal to the image of the function, it is merely required to contain
the image.
コンテントMathML
Content MathML
<apply><eq/> <apply><codomain/><ci>f</ci></apply> <rationals/> </apply>
表示例
Sample Presentation
<mrow> <mrow><mi>codomain</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>f</mi></mfenced></mrow> <mo>=</mo> <mi mathvariant="double-struck">Q</mi> </mrow>
4.4.1.8 像 <image/>
Image <image/>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
image |
image要素は, この要素が適用される関数の像を表します. 関数の像は, 関数によって得られる値の集合です. 像の全ての点は, 定義域の何らかの点に適用された関数によって生み出されます.
The image element represent the image of
the function to which it is applied. The image of a function is the
set of values taken by the function. Every point in the image is
generated by the function applied to some point of the domain.
コンテントMathML
Content MathML
<apply><eq/> <apply><image/><sin/></apply> <interval><cn>-1</cn><cn> 1</cn></interval> </apply>
表示例
Sample Presentation
<mrow> <mrow><mi>image</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>sin</mi></mfenced></mrow> <mo>=</mo> <mfenced open="[" close="]"><mn>-1</mn><mn>1</mn></mfenced> </mrow>
4.4.1.9 区分的関数の定義 <piecewise>, <piece>, <otherwise>
Piecewise declaration <piecewise>, <piece>, <otherwise>
piecewiseに対する構文の表Syntax Table for piecewise
|
pieceに対する構文の表Syntax Table for piece
|
otherwiseに対する構文の表Syntax Table for otherwise
|
piecewise, piece, otherwise要素は, "xが0未満のときH(x) = 0, それ以外のときH(x) = 1"という形の"区分的"関数の定義を表す場合に使用されます.
The piecewise, piece, and otherwise elements are used to
represent "piecewise" function definitions of the form "
H(x) = 0 if x less than 0, H(x) = 1
otherwise".
宣言は, piecewise要素を用いて構築されます. この宣言は, 0個以上のpiece要素と必須でない1個のotherwise要素を含みます. 各piece要素は, ちょうど2つの子要素を含みます. 最初の子要素は, 関連付けられた2番目のpiece子要素で指定された条件が真値の場合に, piecewiseの式が返す値を定義します. 1つもpiece要素やotherwise要素がない退廃した状況では, 定義域の全ての値に対し定義されていないものとして扱われます.
The declaration is constructed using the piecewise element. This contains
zero or more piece elements, and optionally one otherwise element. Each
piece element contains exactly two children. The first child defines the value
taken by the piecewise expression when the condition specified in the associated
second child of the piece is true. The degenerate case of no piece
elements and no otherwise element is treated as undefined for all values of the
domain.
otherwise要素は, どの条件(piece要素の2番目の子要素)も真値でない場合にpiecewise関数が返す値, すなわち既定値の指定を認めています.
The otherwise element allows the specification of a value to be taken by the
piecewise function when none of the conditions (second child elements of the
piece elements) is true, i.e. a default value.
何ら"実行の順序"は, piecewiseの中のpiece子要素の順番によって決められないことに注意すべきです. piece要素の2番目の子要素によって定義される関数の定義域がばらばらであることを, 確かなものにすることは利用者の責任です. また, それらが重なっていたとき, 一致する最初のpiece要素の子要素の値が使用されます. そうでない状況の場合, 式の意味は定義されていません.
It should be noted that no "order of execution" is implied by the
ordering of the piece child elements within piecewise. It is the
responsibility of the author to ensure that the subsets of the function domain defined by
the second children of the piece elements are disjoint, or that, where they
overlap, the values of the corresponding first children of the piece elements
coincide. If this is not the case, the meaning of the expression is
undefined.
ここに例を示します.
Here is an example:
コンテントMathML
Content MathML
<piecewise>
<piece>
<apply><minus/><ci>x</ci></apply>
<apply><lt/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<cn>0</cn>
<apply><eq/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<ci>x</ci>
<apply><gt/><ci>x</ci><cn>0</cn></apply>
</piece>
</piecewise>表示例
Sample Presentation
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd><mrow><mo>−<!--MINUS SIGN--></mo><mi>x</mi></mrow></mtd>
<mtd columnalign="left"><mtext> <!--NO-BREAK SPACE--> if  <!--NO-BREAK SPACE--></mtext></mtd>
<mtd><mrow><mi>x</mi><mo><</mo><mn>0</mn></mrow></mtd>
</mtr>
<mtr>
<mtd><mn>0</mn></mtd>
<mtd columnalign="left"><mtext> <!--NO-BREAK SPACE--> if  <!--NO-BREAK SPACE--></mtext></mtd>
<mtd><mrow><mi>x</mi><mo>=</mo><mn>0</mn></mrow></mtd>
</mtr>
<mtr>
<mtd><mi>x</mi></mtd>
<mtd columnalign="left"><mtext> <!--NO-BREAK SPACE--> if  <!--NO-BREAK SPACE--></mtext></mtd>
<mtd><mrow><mi>x</mi><mo>></mo><mn>0</mn></mrow></mtd>
</mtr>
</mtable>
</mrow>厳格なマークアップへの対応付け
Mapping to Strict Markup
厳格なコンテントMathMLでは, 入れ物要素piecewise, piece, otherwiseは, piece1コンテント辞書の同じ名前の構築子記号の適用に対応付けられます. これらの3つの要素(それぞれの記号)は一緒に使われるという事実とは関係なく, 厳格なマークアップへの対応付けは, すっきりしています.
In Strict Content MathML, the container elements
piecewise, piece and otherwise are mapped
to applications of the constructor symbols of the same names in the
piece1 CD. Apart from the fact that these three
elements (respectively symbols) are used together, the mapping to
Strict markup is straightforward:
コンテントMathML
Content MathML
<piecewise>
<piece>
<cn>0</cn>
<apply><lt/><ci>x</ci><cn>0</cn></apply>
</piece>
<piece>
<cn>1</cn>
<apply><gt/><ci>x</ci><cn>1</cn></apply>
</piece>
<otherwise>
<ci>x</ci>
</otherwise>
</piecewise>等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="piece1">piecewise</csymbol>
<apply><csymbol cd="piece1">piece</csymbol>
<cn>0</cn>
<apply><csymbol cd="relation1">lt</csymbol><ci>x</ci><cn>0</cn></apply>
</apply>
<apply><csymbol cd="piece1">piece</csymbol>
<cn>1</cn>
<apply><csymbol cd="relation1">gt</csymbol><ci>x</ci><cn>1</cn></apply>
</apply>
<apply><csymbol cd="piece1">otherwise</csymbol>
<ci>x</ci>
</apply>
</apply>4.4.2 算数, 代数, 論理
Arithmetic, Algebra and Logic
4.4.2.1 商 <quotient/>
Quotient <quotient/>
| 種類 Class |
binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
quotient |
quotient要素は, 整数の割り算演算子を表します. この演算子が整数の引数aとbに適用されたとき, 結果は, "a割るbの商"になります. つまり, 整数aとbの商は, a = b * q + rといた整数qで, |r|は|b|より小さく, a * rは正となるものです. 一般的な利用で, qは商と呼ばれ, rは余りと呼ばれます.
The quotient element represents the integer division
operator. When the operator is applied to integer arguments
a and b, the result is the "quotient of
a divided by b". That is, the quotient
of integers a and b, is the integer
q such that a = b * q +
r, with |r| less than |b| and
a * r positive. In common usage, q
is called the quotient and r is the remainder.
コンテントMathML
Content MathML
<apply><quotient/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mo>⌊<!--LEFT FLOOR--></mo><mi>a</mi><mo>/</mo><mi>b</mi><mo>⌋<!--RIGHT FLOOR--></mo></mrow>
4.4.2.2 階乗 <factorial/>
Factorial <factorial/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
factorial |
この要素は, 負でない整数での単一項の階乗演算子を表します.
This element represents the unary factorial operator on non-negative integers.
整数nの階乗は, n! = n*(n-1)* ... * 1で与えられます.
The factorial of an integer n is given by n! = n*(n-1)* ... * 1
コンテントMathML
Content MathML
<apply><factorial/><ci>n</ci></apply>
表示例
Sample Presentation
<mrow><mi>n</mi><mo>!</mo></mrow>
4.4.2.3 割り算 <divide/>
Division <divide/>
| 種類 Class |
binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
divide |
divide要素は, 数体での割り算演算子を表します.
The divide element represents the division operator in a
number field.
コンテントMathML
Content MathML
<apply><divide/> <ci>a</ci> <ci>b</ci> </apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>/</mo><mi>b</mi></mrow>
4.4.2.4 最大値 <max/>
Maximum <max/>
| 種類 Class |
nary-minmax |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| OM記号 OM Symbols |
max |
max要素は, この要素が適用された引数の中で最大のものを返す, 最大値関数を示します. それらの引数は, 明確にapply要素で囲まれて指定されるか, 第4.3.4.4節 複数項または単一項の演算子(種類nary-minmax, nary-stats)で説明した, 修飾要素を用いて指定されるかするでしょう. 数が無限である引数の集合に適用される場合, 最大の引数は存在しないであろうことに注意して下さい.
The max element denotes the maximum function, which
returns the largest of the arguments to which it is applied. Its
arguments may be explicitly specified in the enclosing
apply element, or specified using qualifier elements
as described in Section 4.3.4.4 N-ary/Unary Operators (classes nary-minmax, nary-stats). Note that when applied to
infinite sets of arguments, no maximal argument may exist.
コンテントMathML
Content MathML
<apply><max/><cn>2</cn><cn>3</cn><cn>5</cn></apply>
表示例
Sample Presentation
<mrow>
<mi>max</mi>
<mrow>
<mo>{</mo><mn>2</mn><mo>,</mo><mn>3</mn><mo>,</mo><mn>5</mn><mo>}</mo>
</mrow>
</mrow>コンテントMathML
Content MathML
<apply><max/>
<bvar><ci>y</ci></bvar>
<condition>
<apply><in/>
<ci>y</ci>
<interval><cn>0</cn><cn>1</cn></interval>
</apply>
</condition>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>表示例
Sample Presentation
<mrow>
<mi>max</mi>
<mrow>
<mo>{</mo><mi>y</mi><mo>|</mo>
<mrow>
<msup><mi>y</mi><mn>3</mn></msup>
<mo>∈<!--ELEMENT OF--></mo>
<mfenced open="[" close="]"><mn>0</mn><mn>1</mn></mfenced>
</mrow>
<mo>}</mo>
</mrow>
</mrow>4.4.2.5 最小値 <min/>
Minimum <min/>
| 種類 Class |
nary-minmax |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
min |
min要素は, この要素が適用された引数の中で最小のものを返す, 最小値関数を示します. それらの引数は, 明確にapply要素で囲われて指定されるか, 第4.3.4.4節 複数項または単一項の演算子(種類nary-minmax, nary-stats)で説明した, 修飾要素を用いて指定されるかするでしょう. 数が無限である引数の集合に適用される場合, 最小の引数は存在しないであろうことに注意して下さい.
The min element denotes the minimum function, which returns the smallest of
the arguments to which it is applied. Its arguments may be explicitly specified in the
enclosing apply element, or specified using qualifier
elements as described in Section 4.3.4.4 N-ary/Unary Operators (classes nary-minmax, nary-stats). Note that when applied to infinite sets of arguments, no
minimal argument may exist.
コンテントMathML
Content MathML
<apply><min/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow>
<mi>min</mi>
<mrow><mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>}</mo></mrow>
</mrow>コンテントMathML
Content MathML
<apply><min/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><notin/><ci>x</ci><ci type="set">B</ci></apply>
</condition>
<apply><power/><ci>x</ci><cn>2</cn></apply>
</apply>表示例
Sample Presentation
<mrow>
<mi>min</mi>
<mrow><mo>{</mo><msup><mi>x</mi><mn>2</mn></msup><mo>|</mo>
<mrow><mi>x</mi><mo>∉<!--NOT AN ELEMENT OF--></mo><mi>B</mi></mrow>
<mo>}</mo>
</mrow>
</mrow>4.4.2.6 引き算 <minus/>
Subtraction <minus/>
| 種類 Class |
unary-arith, binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
unary_minus, minus |
minus要素は, 単一項の算術演算子としても(つまり, - xを表すためにも), または二項算術演算子としても(つまり, x- yを表すためにも)利用されるでしょう.
The minus element can be used as a unary arithmetic operator
(e.g. to represent - x), or as a binary arithmetic operator
(e.g. to represent x- y).
この要素が1つの引数と一緒に使用される場合, minusはunary_minus記号に対応します.
If it is used with one argument, minus corresponds to the unary_minus symbol.
コンテントMathML
Content MathML
<apply><minus/><cn>3</cn></apply>
表示例
Sample Presentation
<mrow><mo>−<!--MINUS SIGN--></mo><mn>3</mn></mrow>
この要素が2つの引数と一緒に利用される場合, minusはminus記号に対応します.
If it is used with two arguments, minus corresponds to the
minus symbol
コンテントMathML
Content MathML
<apply><minus/><ci>x</ci><ci>y</ci></apply>
表示例
Sample Presentation
<mrow><mi>x</mi><mo>−<!--MINUS SIGN--></mo><mi>y</mi></mrow>
どちらの場合も, 厳格なコンアテントマークアップへの変換は直接, 書き換え: 要素で述べたように行われます. このことは, 単に実際の利用を反映した記号を選ぶだけの問題です.
In both cases, the translation to Strict Content markup is direct, as described in Rewrite: element. It is merely a matter of choosing the symbol that reflects the actual usage.
4.4.2.7 足し算 <plus/>
Addition <plus/>
| 種類 Class |
nary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
plus |
plus要素は, 足し算演算子を表します. その引数は通常, 明確にapply要素で囲まれて指定されます. 複数項の交換法則を満たす演算子として, 引数を指定する修飾要素と一緒に使用できます. しかしながら, このことは避けられるべきで, 代わりにsum演算子がそのような式を表すのに使われるべきです.
The plus element represents the addition operator. Its
arguments are normally specified explicitly in the enclosing
apply element. As an n-ary commutative operator, it can
be used with qualifiers to specify arguments, however,
this is discouraged, and the sum operator should be
used to represent such expressions instead.
コンテントMathML
Content MathML
<apply><plus/><ci>x</ci><ci>y</ci><ci>z</ci></apply>
表示例
Sample Presentation
<mrow><mi>x</mi><mo>+</mo><mi>y</mi><mo>+</mo><mi>z</mi></mrow>
4.4.2.8 指数 <power/>
Exponentiation <power/>
| 種類 Class |
binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
power |
power要素は, 指数演算子を表します. 最初の引数が, 2番目の引数である次数まで累乗されます.
The power element represents the exponentiation
operator. The first argument is raised to the power of the second
argument.
コンテントMathML
Content MathML
<apply><power/><ci>x</ci><cn>3</cn></apply>
表示例
Sample Presentation
<msup><mi>x</mi><mn>3</mn></msup>
4.4.2.9 余り <rem/>
Remainder <rem/>
| 種類 Class |
binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
remainder |
rem要素は, 最初の引数を2番目の引数で割ったときの余りを返す標準的な演算子を表します. つまり, 整数の引数aとbに適用された場合, a = b * q + rといった式で, |r|が|b|より小さく, a * rが正となる唯一の整数rを返します.
The rem element represents the modulus operator, which
returns the remainder that results from dividing the first argument by
the second. That is, when applied to integer arguments a
and b, it returns the unique integer r such that
a = b * q + r, with
|r| less than |b| and a *
r positive.
コンテントMathML
Content MathML
<apply><rem/><ci> a </ci><ci> b </ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>mod</mo><mi>b</mi></mrow>
4.4.2.10 掛け算 <times/>
Multiplication <times/>
| 種類 Class |
nary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
times |
times要素は, 複数項の掛け算演算子を表します. その引数は通常, 明確にapply要素で囲まれて指定されます. 複数項の交換法則を満たす演算子として, 決まりに基づいて引数を指定する修飾要素と一緒に使用できます. しかしながら, このことは避けられるべきで, 代わりにproduct演算子がそのような式を表すのに使われるべきです.
The times element represents the n-ary multiplication operator. Its
arguments are normally specified explicitly in the enclosing
apply element. As an n-ary commutative operator, it can
be used with qualifiers to specify arguments by rule, however,
this is discouraged, and the product operator should be
used to represent such expressions instead.
コンテントMathML
Content MathML
<apply><times/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>b</mi></mrow>
4.4.2.11 根 <root/>
Root <root/>
| 種類 Class |
unary-arith, binary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
degree |
| OM記号 OM Symbols |
root |
root要素は, 根を求めるのに使用されます. 用いられる根の種類は"degree"要素で指定し, その要素は, root要素を囲っているapply要素の2番目の子要素として与えられるべきです. よって, 平方根はdegreeが値2を含んでいる場合に相当し, 立方根は3に相当しといった具合です. degreeが存在しない場合, 既定値の2が使用されます.
The root element is used to extract roots. The kind of root to be taken is
specified by a "degree" element, which should be given as the second child of
the apply element enclosing the root element. Thus, square roots
correspond to the case where degree contains the value 2, cube roots
correspond to 3, and so on. If no degree is present, a default value of 2 is
used.
コンテントMathML
Content MathML
<apply><root/> <degree><ci type="integer">n</ci></degree> <ci>a</ci> </apply>
表示例
Sample Presentation
<mroot><mi>a</mi><mi>n</mi></mroot>
厳格なコンテントマークアップへの対応付け
Mapping to Strict Content Markup
厳格なコンテントマークアップでは, root記号がいつも2つの引数と一緒に使用され, 2番目の引数が, 生成された根の次数を示します.
In Strict Content markup, the root symbol is always used with two arguments, with the second indicating the degree of the root being extracted.
コンテントMathML
Content MathML
<apply><root/><ci>x</ci></apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="arith1">root</csymbol> <ci>x</ci> <cn type="integer">2</cn> </apply>
コンテントMathML
Content MathML
<apply><root/> <degree><ci type="integer">n</ci></degree> <ci>a</ci> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="arith1">root</csymbol> <ci>a</ci> <cn type="integer">n</cn> </apply>
4.4.2.12 最大公約数 <gcd/>
Greatest common divisor <gcd/>
| 種類 Class |
nary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
gcd |
gcd要素は, 引数の最大公約数を返す複数項の演算子を表します. それらの引数は, 明確にapply要素で囲まれて指定されるか, 第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で述べた決まりによって指定されるでしょう.
The gcd element represents the n-ary operator which returns
the greatest common divisor of its arguments. Its
arguments may be explicitly specified in the enclosing
apply element, or specified by rule as described in
Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
コンテントMathML
Content MathML
<apply><gcd/><ci>a</ci><ci>b</ci><ci>c</ci></apply>
表示例
Sample Presentation
<mrow> <mi>gcd</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>a</mi><mi>b</mi><mi>c</mi></mfenced> </mrow>
この通常の描画は英語圏特有のものです. 他の場所では, 通常の描画は違ったものとなるでしょう.
This default rendering is English-language locale specific: other locales may have different default renderings.
gcd要素が引数の明確な一覧に適用されるとき, 厳格なコンテントマークアップへの変換は直接, gcd記号を用いて, 書き換え: 要素で説明したように行われます. ただし, 修飾要素が使われている場合, 等価な厳格なマークアップは, 書き換え: 複数項の演算子 domainofapplicationを通じて計算されたものになります.
When the gcd element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the gcd symbol, as described in Rewrite: element. However, when
qualifiers are used, the equivalent Strict markup is computed via
Rewrite: n-ary domainofapplication.
4.4.2.13 論理積 <and/>
And <and/>
| 種類 Class |
nary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
and |
and要素は, ブール値の引数を受け取り, ブール値の値を返す複数項の関数である"論理積"関数を表します. 全ての引数が真値の場合は真値を返し, そうでない場合は偽値を返します. この関数の引数は, apply要素で囲まれて明確に指定されるか, 第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で述べた決まりに基づいて指定されるでしょう.
The and element represents the logical "and" function which is
an n-ary function taking Boolean arguments and returning a Boolean value. It is true if
all arguments are true, and false otherwise. Its arguments may be explicitly specified
in the enclosing apply element, or specified by rule as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
コンテントMathML
Content MathML
<apply><and/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>∧<!--LOGICAL AND--></mo><mi>b</mi></mrow>
コンテントMathML
Content MathML
<apply><and/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><ci>n</ci></uplimit> <apply><gt/><apply><selector/><ci>a</ci><ci>i</ci></apply><cn>0</cn></apply> </apply>
厳格なコンテントMathML
Strict Content MathML
<apply><csymbol cd="fns2">apply_to_list</csymbol>
<csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="list1">map</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="relation1">gt</csymbol>
<apply><csymbol cd="linalg1">vector_selector</csymbol>
<ci>i</ci>
<ci>a</ci>
</apply>
<cn>0</cn>
</apply>
</bind>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn type="integer">0</cn>
<ci>n</ci>
</apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <munderover> <mo>⋀<!--N-ARY LOGICAL AND--></mo> <mrow><mi>i</mi><mo>=</mo><mn>0</mn></mrow> <mi>n</mi> </munderover> <mrow> <mo>(</mo> <msub><mi>a</mi><mi>i</mi></msub> <mo>></mo> <mn>0</mn> <mo>)</mo> </mrow> </mrow>
4.4.2.14 論理和 <or/>
Or <or/>
| 種類 Class |
nary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
or |
or要素は, "論理和"関数を表します. 引数のどれかが真値の場合は真値を返し, そうでない場合は偽値を返します.
The or element represents the logical "or" function. It is
true if any of the arguments are true, and false otherwise.
コンテントMathML
Content MathML
<apply><or/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>∨<!--LOGICAL OR--></mo><mi>b</mi></mrow>
4.4.2.15 排他論理和 <xor/>
Exclusive Or <xor/>
| 種類 Class |
nary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
xor |
xor要素は, "排他論理和"関数を表します. 真値である引数の数が奇数の場合は真値を返し, そうでない場合は偽値を返します.
The xor element represents the logical "xor"
function. It is true if there are an odd number of true arguments or
false otherwise.
コンテントMathML
Content MathML
<apply><xor/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>xor</mo><mi>b</mi></mrow>
4.4.2.16 否定 <not/>
Not <not/>
| 種類 Class |
unary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
not |
not要素は, 1つのブール値の引数を受け取り, 逆のブール値の値を返す論理的否定関数を表します.
The not element represents the logical not function
which takes one Boolean argument, and returns the opposite Boolean
value.
コンテントMathML
Content MathML
<apply><not/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mo>¬<!--NOT SIGN--></mo><mi>a</mi></mrow>
4.4.2.17 含意 <implies/>
Implies <implies/>
| 種類 Class |
binary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
implies |
implies要素は, 2つのブール値の式を引数に受け取る論理的含意関数を表します. 最初の引数が真値で, 2番目の引数が偽値の場合, この関数は偽値と評価し, そうでない場合は真値と評価します.
The implies element represents the logical implication
function which takes two Boolean expressions as arguments. It
evaluates to false if the first argument is true and the second
argument is false, otherwise it evaluates to true.
コンテントMathML
Content MathML
<apply><implies/><ci>A</ci><ci>B</ci></apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⇒<!--RIGHTWARDS DOUBLE ARROW--></mo><mi>B</mi></mrow>
4.4.2.18 全称記号 <forall/>
Universal quantifier <forall/>
| 種類 Class |
quantifier |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
forall, implies |
forall要素は, 1つ以上の束縛変数と量化された主張を指定する引数から成る全称記号("全ての")を表します. 加えて, 第4.3.4.8節 量化記号(種類quantifier)で説明したconditionまたは他の修飾要素が, 束縛変数の定義域を制限するために利用されるかもしれません.
The forall element represents the universal ("for all")
quantifier which takes one or more bound variables, and an
argument which specifies the assertion being quantified.
In addition, condition or other qualifiers may be used as
described in Section 4.3.4.8 Quantifiers (class quantifier) to limit the domain
of the bound variables.
コンテントMathML
Content MathML
<bind><forall/>
<bvar><ci>x</ci></bvar>
<apply><eq/>
<apply><minus/><ci>x</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</bind>表示例
Sample Presentation
<mrow> <mo>∀<!--FOR ALL--></mo> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mrow><mi>x</mi><mo>−<!--MINUS SIGN--></mo><mi>x</mi></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
forall要素がcondition修飾要素と一緒に使用される場合, 等価な厳格なマークアップは, 書き換え: 量化記号の決まりによる論理的含意に手助けされながら構築されます.
When the forall element is used with a condition qualifier the
strict equivalent is constructed with the help of logical implication by the rule
Rewrite: quantifier. Thus
<bind><forall/>
<bvar><ci>p</ci></bvar>
<bvar><ci>q</ci></bvar>
<condition>
<apply><and/>
<apply><in/><ci>p</ci><rationals/></apply>
<apply><in/><ci>q</ci><rationals/></apply>
<apply><lt/><ci>p</ci><ci>q</ci></apply>
</apply>
</condition>
<apply><lt/>
<ci>p</ci>
<apply><power/><ci>q</ci><cn>2</cn></apply>
</apply>
</bind>よって, この式は次のように変換されます.
translates to
<bind><csymbol cd="quant1">forall</csymbol>
<bvar><ci>p</ci></bvar>
<bvar><ci>q</ci></bvar>
<apply><csymbol cd="logic1">implies</csymbol>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="set1">in</csymbol>
<ci>p</ci>
<csymbol cd="setname1">Q</csymbol>
</apply>
<apply><csymbol cd="set1">in</csymbol>
<ci>q</ci>
<csymbol cd="setname1">Q</csymbol>
</apply>
<apply><csymbol cd="relation1">lt</csymbol><ci>p</ci><ci>q</ci></apply>
</apply>
<apply><csymbol cd="relation1">lt</csymbol>
<ci>p</ci>
<apply><csymbol cd="arith1">power</csymbol>
<ci>q</ci>
<cn>2</cn>
</apply>
</apply>
</apply>
</bind>表示例
Sample Presentation
<mrow> <mo>∀<!--FOR ALL--></mo> <mrow> <mrow><mi>p</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Q</mi></mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow><mi>q</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Q</mi></mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow><mo>(</mo><mi>p</mi><mo><</mo><mi>q</mi><mo>)</mo></mrow> </mrow> <mo>.</mo> <mfenced> <mrow><mi>p</mi><mo><</mo><msup><mi>q</mi><mn>2</mn></msup></mrow> </mfenced> </mrow>
<mrow> <mo>∀<!--FOR ALL--></mo> <mrow><mi>p</mi><mo>,</mo><mi>q</mi></mrow> <mo>.</mo> <mfenced> <mrow> <mrow> <mo>(</mo> <mrow> <mi>p</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Q</mi> </mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow> <mi>q</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Q</mi> </mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow><mo>(</mo><mi>p</mi><mo><</mo><mi>q</mi><mo>)</mo></mrow> <mo>)</mo> </mrow> <mo>⇒<!--RIGHTWARDS DOUBLE ARROW--></mo> <mrow> <mo>(</mo> <mi>p</mi> <mo><</mo> <msup><mi>q</mi><mn>2</mn></msup> <mo>)</mo> </mrow> </mrow> </mfenced> </mrow>
4.4.2.19 存在記号 <exists/>
Existential quantifier <exists/>
| 種類 Class |
quantifier |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
exists, and |
exists要素は, 1つ以上の束縛変数と量化された主張を指定する引数から成る存在記号("存在する")を表します. 加えて, 第4.3.4.8節 量化記号(種類quantifier)で説明したconditionまたは他の修飾要素が, 束縛変数の定義域を制限するために利用されるかもしれません.
The exists element represents the existential ("there exists")
quantifier which takes one or more bound variables, and an
argument which specifies the assertion being quantified. In
addition, condition or other qualifiers may be used as
described in Section 4.3.4.8 Quantifiers (class quantifier) to limit the domain
of the bound variables.
コンテントMathML
Content MathML
<bind><exists/>
<bvar><ci>x</ci></bvar>
<apply><eq/>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</bind>表示例
Sample Presentation
<mrow> <mo>∃<!--THERE EXISTS--></mo> <mi>x</mi> <mo>.</mo> <mfenced> <mrow> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
コンテントMathML
Content MathML
<apply><exists/>
<bvar><ci>x</ci></bvar>
<domainofapplication>
<integers/>
</domainofapplication>
<apply><eq/>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</apply>等価な厳格なMathML
Strict MathML equivalent:
<bind><csymbol cd="quant1">exists</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="set1">in</csymbol>
<ci>x</ci>
<csymbol cd="setname1">Z</csymbol>
</apply>
<apply><csymbol cd="relation1">eq</csymbol>
<apply><ci>f</ci><ci>x</ci></apply>
<cn>0</cn>
</apply>
</apply>
</bind>表示例
Sample Presentation
<mrow> <mo>∃<!--THERE EXISTS--></mo> <mi>x</mi> <mo>.</mo> <mfenced separators=""> <mrow><mi>x</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Z</mi></mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> <mo>=</mo> <mn>0</mn> </mrow> </mfenced> </mrow>
4.4.2.20 絶対値 <abs/>
Absolute Value <abs/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
abs |
abs要素は, 絶対値関数を表します. 引数は, 数値の値であるべきです. 引数が複素数の場合, 絶対値はしばしば, 0点からの距離として参照されます(訳注:原文ではmodulusで, 複素数の絶対値ですが, 絶対値という言葉が繰り返されることからこのような表現にしています).
The abs element represents the absolute value
function. The argument should be numerically valued. When the
argument is a complex number, the absolute value is often referred
to as the modulus.
コンテントMathML
Content MathML
<apply><abs/><ci>x</ci></apply>
表示例
Sample Presentation
<mrow><mo>|</mo><mi>x</mi><mo>|</mo></mrow>
4.4.2.21 共役複素数 <conjugate/>
Complex conjugate <conjugate/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
conjugate |
conjugate要素は, 引数の共役複素数を表す複素数で定義された関数を表します.
The conjugate element represents the function defined
over the complex numbers with returns the complex conjugate of
its argument.
コンテントMathML
Content MathML
<apply><conjugate/>
<apply><plus/>
<ci>x</ci>
<apply><times/><cn>ⅈ<!--DOUBLE-STRUCK ITALIC SMALL I--></cn><ci>y</ci></apply>
</apply>
</apply>表示例
Sample Presentation
<mover> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mn>ⅈ<!--DOUBLE-STRUCK ITALIC SMALL I--></mn><mo>⁢<!--INVISIBLE TIMES--></mo><mi>y</mi></mrow> </mrow> <mo>¯<!--MACRON--></mo> </mover>
4.4.2.22 偏角 <arg/>
Argument <arg/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
argument |
arg要素は, 複素数の角度, すなわち, その数から0に向かって引いた直線と, 実数の数直線のなす(反時計回りに測った)角度を返す単一項の関数です.
The arg element represents the unary function which
returns the angular argument of a complex number, namely the
angle which a straight line drawn from the number to zero makes
with the real line (measured anti-clockwise).
コンテントMathML
Content MathML
<apply><arg/>
<apply><plus/>
<ci> x </ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mi>arg</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.23 実数部分 <real/>
Real part <real/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
real |
real要素は, 複素数の"実数"部分, すなわち, x + iyのx成分を表す式を構築するのに使われる単一項の演算子を表します.
The real element represents the unary operator used to
construct an expression representing the "real" part of a
complex number, that is, the x component in x + iy.
コンテントMathML
Content MathML
<apply><real/>
<apply><plus/>
<ci>x</ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mo>ℛ<!--SCRIPT CAPITAL R--></mo> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.24 虚数部分 <imaginary/>
Imaginary part <imaginary/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
imaginary |
imaginary要素は, 複素数の"虚数"部分, すなわち, x + iyのy成分を表す式を構築するのに使われる単一項の演算子を表します.
The imaginary element represents the unary operator used to
construct an expression representing the "imaginary" part of a
complex number, that is, the y component in x + iy.
コンテントMathML
Content MathML
<apply><imaginary/>
<apply><plus/>
<ci>x</ci>
<apply><times/><imaginaryi/><ci>y</ci></apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mo>ℑ<!--BLACK-LETTER CAPITAL I--></mo> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced> <mrow> <mi>x</mi> <mo>+</mo> <mrow><mi>i</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>y</mi></mrow> </mrow> </mfenced> </mrow>
4.4.2.25 最小公倍数 <lcm/>
Lowest common multiple <lcm/>
| 種類 Class |
nary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
lcm |
lcm要素は, 引数の最小公倍数を表す式を構築するのに使われる複数項の演算子を表します. 何も引数が与えられない場合, lcmは1です. 1つの引数が与えられた場合, lcmはその引数になります. xと1の最小公倍数はxです.
The lcm element represents the n-ary operator used to
construct an expression which represents the least common multiple
of its arguments. If no argument is provided, the lcm is 1. If one
argument is provided, the lcm is that argument. The least common
multiple of x and 1 is x.
コンテントMathML
Content MathML
<apply><lcm/><ci>a</ci><ci>b</ci><ci>c</ci></apply>
表示例
Sample Presentation
<mrow> <mi>lcm</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>a</mi><mi>b</mi><mi>c</mi></mfenced> </mrow>
この通常の描画は英語圏特有のものです. 他の場所では, 通常の描画は違ったものとなるでしょう.
This default rendering is English-language locale specific: other locales may have different default renderings.
4.4.2.26 切り捨て <floor/>
Floor <floor/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
floor |
floor要素は, 最も近い整数に(負の無限大の方向に)切り捨てる操作を表します. この関数は, 引数に1つの実数を受け取り, 整数を返します.
The floor element represents the operation that rounds
down (towards negative infinity) to the nearest integer. This
function takes one real number as an argument and returns an
integer.
コンテントMathML
Content MathML
<apply><floor/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mo>⌊<!--LEFT FLOOR--></mo><mi>a</mi><mo>⌋<!--RIGHT FLOOR--></mo></mrow>
4.4.2.27 切り上げ <ceiling/>
Ceiling <ceiling/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
ceiling |
ceiling要素は, 最も近い整数に(正の無限大の方向に)切り上げる操作を表します. この関数は, 引数に1つの実数を受け取り, 整数を返します.
The ceiling element represents the operation that rounds
up (towards positive infinity) to the nearest integer. This function
takes one real number as an argument and returns an integer.
コンテントMathML
Content MathML
<apply><ceiling/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mo>⌈<!--LEFT CEILING--></mo><mi>a</mi><mo>⌉<!--RIGHT CEILING--></mo></mrow>
4.4.3 関係
Relations
4.4.3.1 等しい <eq/>
Equals <eq/>
| 種類 Class |
nary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
eq |
eq要素は, 等しい関係を表します. 等号は2項の関係である一方, eqは, 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, 一連の等号を記載して, 2つより多い引数と一緒に使われるかもしれません.
The eq elements represents the equality relation. While equality is a binary relation,
eq may be used with more than two arguments, denoting a chain
of equalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
コンテントMathML
Content MathML
<apply><eq/> <cn type="rational">2<sep/>4</cn> <cn type="rational">1<sep/>2</cn> </apply>
表示例
Sample Presentation
<mrow> <mrow><mn>2</mn><mo>/</mo><mn>4</mn></mrow> <mo>=</mo> <mrow><mn>1</mn><mo>/</mo><mn>2</mn></mrow> </mrow>
4.4.3.2 等しくない <neq/>
Not Equals <neq/>
| 種類 Class |
binary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
neq |
neq要素は, 2項の不等式関係, すなわち, 2つの引数が等しくない限り真値を返す"等しくない"関係を表します.
The neq element represents the binary inequality
relation, i.e. the relation "not equal to" which returns true unless
the two arguments are equal.
コンテントMathML
Content MathML
<apply><neq/><cn>3</cn><cn>4</cn></apply>
表示例
Sample Presentation
<mrow><mn>3</mn><mo>≠<!--NOT EQUAL TO--></mo><mn>4</mn></mrow>
4.4.3.3 大なり <gt/>
Greater than <gt/>
| 種類 Class |
nary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
gt |
gt要素は, 最初の引数が2番目より大きい場合に真値を, そうでない場合に偽値を返す"大なり"関数を表します. この記号は2項の関係である一方, gtは, 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, 一連の不等号を記載して, 2つより多い引数と一緒に使われるかもしれません.
The gt element represents the "greater than" function
which returns true if the first argument is greater than the second, and
returns false otherwise. While this is a binary relation,
gt may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
コンテントMathML
Content MathML
<apply><gt/><cn>3</cn><cn>2</cn></apply>
表示例
Sample Presentation
<mrow><mn>3</mn><mo>></mo><mn>2</mn></mrow>
4.4.3.4 小なり <lt/>
Less Than <lt/>
| 種類 Class |
nary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
lt |
lt要素は, 最初の引数が2番目より小さい場合に真値を, そうでない場合に偽値を返す"小なり"関数を表します. この記号は2項の関係である一方, ltは, 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, 一連の不等号を記載して, 2つより多い引数と一緒に使われるかもしれません.
The lt element represents the "less than" function
which returns true if the first argument is less than the second, and
returns false otherwise. While this is a binary relation,
lt may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
コンテントMathML
Content MathML
<apply><lt/><cn>2</cn><cn>3</cn><cn>4</cn></apply>
表示例
Sample Presentation
<mrow><mn>2</mn><mo><</mo><mn>3</mn><mo><</mo><mn>4</mn></mrow>
4.4.3.5 大なりまたは等しい <geq/>
Greater Than or Equal <geq/>
| 種類 Class |
nary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
geq |
geq要素は, 最初の引数が2番目より大きいか等しい場合に真値を, そうでない場合に偽値を返す"大なりまたは等しい"関数を表します. この記号は2項の関係である一方, geqは, 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, 一連の不等号を記載して, 2つより多い引数と一緒に使われるかもしれません.
The geq element represents the "greater than or equal to" function
which returns true if the first argument is greater than or equal to
the second, and returns false otherwise. While this is a binary relation,
geq may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
コンテントMathML
Content MathML
<apply><geq/><cn>4</cn><cn>3</cn><cn>3</cn></apply>
厳格なコンテントMathML
Strict Content MathML
<apply><csymbol cd="fns2">predicate_on_list</csymbol> <csymbol cd="reln1">geq</csymbol> <apply><csymbol cd="list1">list</csymbol> <cn>4</cn><cn>3</cn><cn>3</cn> </apply> </apply>
表示例
Sample Presentation
<mrow><mn>4</mn><mo>≥<!--GREATER-THAN OR EQUAL TO--></mo><mn>3</mn><mo>≥<!--GREATER-THAN OR EQUAL TO--></mo><mn>3</mn></mrow>
4.4.3.6 小なりまたは等しい <leq/>
Less Than or Equal <leq/>
| 種類 Class |
nary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
leq |
leq要素は, 最初の引数が2番目より小さいか等しい場合に真値を, そうでない場合に偽値を返す"小なりまたは等しい"関数を表します. この記号は2項の関係である一方, leqは, 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, 一連の不等号を記載して, 2つより多い引数と一緒に使われるかもしれません.
The leq element represents the "less than or equal to" function
which returns true if the first argument is less than or equal to
the second, and returns false otherwise. While this is a binary relation,
leq may be used with more than two arguments, denoting a chain
of inequalities, as described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln).
コンテントMathML
Content MathML
<apply><leq/><cn>3</cn><cn>3</cn><cn>4</cn></apply>
表示例
Sample Presentation
<mrow><mn>3</mn><mo>≤<!--LESS-THAN OR EQUAL TO--></mo><mn>3</mn><mo>≤<!--LESS-THAN OR EQUAL TO--></mo><mn>4</mn></mrow>
4.4.3.7 同値 <equivalent/>
Equivalent <equivalent/>
| 種類 Class |
binary-logical |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
equivalent |
equivalent要素は, 2つのブール値の式が論理的に同値であると断定する関係を表します. 同値であるとは, どんな入力に対しても同じブール値となることです.
The equivalent element represents the relation that
asserts two Boolean expressions are logically equivalent,
that is have the same Boolean value for any inputs.
コンテントMathML
Content MathML
<apply><equivalent/> <ci>a</ci> <apply><not/><apply><not/><ci>a</ci></apply></apply> </apply>
表示例
Sample Presentation
<mrow> <mi>a</mi> <mo>≡<!--IDENTICAL TO--></mo> <mrow><mo>¬<!--NOT SIGN--></mo><mrow><mo>¬<!--NOT SIGN--></mo><mi>a</mi></mrow></mrow> </mrow>
4.4.3.8 近似 <approx/>
Approximately <approx/>
| 種類 Class |
binary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
approx |
approx要素は, 引数がおよそ等しいと断定する関係を表します.
The approx element represent the relation that asserts
the approximate equality of its arguments.
コンテントMathML
Content MathML
<apply><approx/> <pi/> <cn type="rational">22<sep/>7</cn> </apply>
表示例
Sample Presentation
<mrow> <mi>π<!--GREEK SMALL LETTER PI--></mi> <mo>≃<!--ASYMPTOTICALLY EQUAL TO--></mo> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> </mrow>
4.4.3.9 因子 <factorof/>
Factor Of <factorof/>
| 種類 Class |
binary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
factorof |
factorof要素は, 最初の引数が2番目の"因子である"数学的関係を示すのに使われます. この関係は, b mod a = 0の場合にのみ真値を返します.
The factorof element is used to indicate the
mathematical relationship that the first argument "is a factor of"
the second. This relationship is true if and only
if b mod a = 0.
コンテントMathML
Content MathML
<apply><factorof/><ci>a</ci><ci>b</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>|</mo><mi>b</mi></mrow>
4.4.4 微積分とベクトル解析
Calculus and Vector Calculus
4.4.4.1 積分 <int/>
Integral <int/>
| 種類 Class |
int |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
int defint |
int要素は, 関数の定積分または不定積分, もしくは束縛変数を持つ式の定積分のための演算子要素です.
The int element is the operator element for a definite or indefinite integral
over a function or a definite over an expression with a bound variable.
コンテントMathML
Content MathML
<apply><eq/> <apply><int/><sin/></apply> <cos/> </apply>
表示例
Sample Presentation
<mrow><mrow><mi>∫<!--INTEGRAL--></mi><mi>sin</mi></mrow><mo>=</mo><mi>cos</mi></mrow>
コンテントMathML
Content MathML
<apply><int/> <interval><ci>a</ci><ci>b</ci></interval> <cos/> </apply>
表示例
Sample Presentation
<mrow> <msubsup><mi>∫<!--INTEGRAL--></mi><mi>a</mi><mi>b</mi></msubsup><mi>cos</mi> </mrow>
int要素は, 積分変数の役割を果たす束縛変数とも一緒に利用できます.
The int element can also be used with bound variables serving as the
integration variables.
コンテントMathML
Content MathML
ここで, 定積分は, 積分の範囲を指定する修飾要素(ここではlowlimit/uplimitの組み)を提供することで示されます. この書き方は, おそらく定積分の最も"標準的な"表現でしょう.
Here, definite integrals are indicated by providing qualifier elements specifying a
domain of integration (here a lowlimit/uplimit pair). This is perhaps
the most "standard" representation of this integral:
<apply><int/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>1</cn></uplimit> <apply><power/><ci>x</ci><cn>2</cn></apply> </apply>
表示例
Sample Presentation
<mrow> <msubsup><mi>∫<!--INTEGRAL--></mi><mn>0</mn><mn>1</mn></msubsup> <msup><mi>x</mi><mn>2</mn></msup> <mi>d</mi> <mi>x</mi> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
不定積分が関数に適用される場合, int要素は, calculus1コンテント辞書のint記号に対応します. 定積分が関数に適用される場合, int要素は, calculus1コンテント辞書のdefint記号に対応します.
As an indefinite integral applied to a function, the int element corresponds to
the int symbol from the calculus1 content
dictionary. As a definite integral applied to a function, the int element
corresponds to the defint symbol
from the calculus1 content dictionary.
何も束縛変数が存在しない場合, 不定積分の厳格なコンテントMathMLへの変換は単純です. 束縛変数が存在する場合, 次の決まりが使われるべきです.
When no bound variables are present, the translation of an indefinite integral to Strict Content Markup is straight forward. When bound variables are present, the following rule should be used.
書き換え: int
Rewrite: int
が束縛変数 を含む任意の式である, 次の不定積分があるとします.
Translate an indefinite integral, where
is an
arbitrary expression involving the bound variable(s)
<apply><int/> <bvar> </bvar> </apply>
この式は, 次の式に変換されます.
to the expression
<apply>
<apply><csymbol cd="calculus1">int</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>xは元の不定積分の中で束縛されていないため, 例え, 変数xが引数としてintに使われる式の一部で束縛されていたとしても, 厳格なコンテントMathMLで明確な自由変数である変数xに, 積分された関数は適用されることに注意して下さい.
Note that as x is not bound in the original indefinite integral, the integrated function is applied to the variable x making it an explicit free variable in Strict Content Markup expression, even though it is bound in the subterm used as an argument to int.
例えば, 次の式があるとします.
For instance, the expression
<apply><int/> <bvar><ci>x</ci></bvar> <apply><cos/><ci>x</ci></apply> </apply>
この式は, 次の厳格なコンテントMathMLと等価です.
has the Strict Content MathML equivalent
<apply>
<apply><csymbol cd="calculus1">int</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><cos/><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>
束縛変数を伴わない定積分でも, 変換は単純です.
For a definite integral without bound variables, the translation is also straightforward.
例えば, 次のように表される, 任意の領域Cでの微分形式fの積分があるとします.
For instance, the integral of a differential form f over an arbitrary domain C represented as
<apply><int/> <domainofapplication><ci>C</ci></domainofapplication> <ci>f</ci> </apply>
この式は, 次の厳格なコンテントMathMLと等価です.
is equivalent to the Strict Content MathML:
<apply><csymbol cd="calculus1">defint</csymbol><ci>C</ci><ci>f</ci></apply>
ただし, 後で示す定積分での決まりに基づいて積分範囲を指定するのに用いられる, 他の種類の修飾要素の変換に追加の注意が必要です.
Note, however, the additional remarks on the translations of other kinds of qualifiers that may be used to specify a domain of integration in the rules for definite integrals following.
束縛変数が存在する場合, 状況は一般により複雑で, 次の決まりが用いられます.
When bound variables are present, the situation is more complicated in general, and the following rules are used.
書き換え: defint
Rewrite: defint
が束縛変数 を含む任意の式である, 次の定積分があるとします.
Translate a definite integral, where
is an
arbitrary expression involving the bound variable(s)
<apply><int/> <bvar> </bvar> <domainofapplication> </domainofapplication> </apply>
この式は, 次の式に変換されます.
to the expression
<apply><csymbol cd="calculus1">defint</csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
ただし, lowlimit/uplimitの組みを持つ定積分は, 積分範囲を方向付ける強い意味合いを持っており, そのため, 下限と上限を入れ替えることは, 結果の符号を変えることになるでしょう. このことに適応するため, 次の特別な決まりが使われます.
But the definite integral with an lowlimit/uplimit pair carries the
strong intuition that the range of integration is oriented, and thus swapping lower and
upper limits will change the sign of the result. To accommodate this, use the following special
translation rule:
書き換え: defint 極限
Rewrite: defint limits
<apply><int/> <bvar> </bvar> <lowlimit> </lowlimit> <uplimit> </uplimit> </apply>
が変数xの式であるこの式は, 次の式に変換されます.
where
is an expression in the variable x
is translated to to the expression:
<apply><csymbol cd="calculus1">defint</csymbol>
<apply><csymbol cd="interval1">oriented_interval</csymbol>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>oriented_interval記号は, interval修飾要素が変換されたときや, 積分範囲を指定するときにも使われます. 積分は, 左側の端点から右側の端点に向かって行われると想定されています.
The oriented_interval
symbol is also used when translating the interval
qualifier, when it is used to specify the domain of integration.
Integration is assumed to proceed from the left endpoint to the
right endpoint.
多重積分の場合も同じように扱われます.
The case for multiple integrands is treated analogously.
condition修飾要素の利用も特別な取扱いを必要とすることに注意して下さい. 特に, condition修飾要素は, 次の式と同様に追加の束縛変数とデカルト平面に対応した範囲を利用することで, 多変量の範囲に拡張されます.
Note that use of the condition
qualifier also
requires special treatment. In particular, it extends to multivariate domains by
using extra bound variables and a domain corresponding to a cartesian product as in:
<bind><int/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<condition>
<apply><and/>
<apply><leq/><cn>0</cn><ci>x</ci></apply>
<apply><leq/><ci>x</ci><cn>1</cn></apply>
<apply><leq/><cn>0</cn><ci>y</ci></apply>
<apply><leq/><ci>y</ci><cn>1</cn></apply>
</apply>
</condition>
<apply><times/>
<apply><power/><ci>x</ci><cn>2</cn></apply>
<apply><power/><ci>y</ci><cn>3</cn></apply>
</apply>
</bind>等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="calculus1">defint</csymbol>
<apply><csymbol cd="set1">suchthat</csymbol>
<apply><csymbol cd="set1">cartesianproduct</csymbol>
<csymbol cd="setname1">R</csymbol>
<csymbol cd="setname1">R</csymbol>
</apply>
<apply><csymbol cd="logic1">and</csymbol>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>x</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>x</ci><cn>1</cn></apply>
<apply><csymbol cd="arith1">leq</csymbol><cn>0</cn><ci>y</ci></apply>
<apply><csymbol cd="arith1">leq</csymbol><ci>y</ci><cn>1</cn></apply>
</apply>
<bind><csymbol cd="fns11">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<apply><csymbol cd="arith1">times</csymbol>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><cn>2</cn></apply>
<apply><csymbol cd="arith1">power</csymbol><ci>y</ci><cn>3</cn></apply>
</apply>
</bind>
</apply>
</apply>4.4.4.2 微分 <diff/>
Differentiation <diff/>
| 種類 Class |
Differential-Operator |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
diff |
diff要素は, 単独の変数の関数または式に対する微分演算子要素です. この要素は, 元の関数の導関数である関数を示すことによって, 実際の関数に適用されたり, 単独の変数を含む式に適用されたりするでしょう.
The diff element is the differentiation operator element for functions or
expressions of a single variable. It may be applied directly to an actual function
thereby denoting a function which is the derivative of the original function, or it can be
applied to an expression involving a single variable.
コンテントMathML
Content MathML
<apply><diff/><ci>f</ci></apply>
表示例
Sample Presentation
<msup><mi>f</mi><mo>′<!--PRIME--></mo></msup>
コンテントMathML
Content MathML
<apply><eq/>
<apply><diff/>
<bvar><ci>x</ci></bvar>
<apply><sin/><ci>x</ci></apply>
</apply>
<apply><cos/><ci>x</ci></apply>
</apply>表示例
Sample Presentation
<mrow> <mfrac> <mrow><mi>d</mi><mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow></mrow> <mrow><mi>d</mi><mi>x</mi></mrow> </mfrac> <mo>=</mo> <mrow><mi>cos</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow> </mrow>
bvar要素は, 適用される微分係数の階数を指定するdegree要素を含むこともあるでしょう.
The bvar element may also contain a degree element, which specifies
the order of the derivative to be taken.
コンテントMathML
Content MathML
<apply><diff/> <bvar><ci>x</ci><degree><cn>2</cn></degree></bvar> <apply><power/><ci>x</ci><cn>4</cn></apply> </apply>
表示例
Sample Presentation
<mfrac> <mrow> <msup><mi>d</mi><mn>2</mn></msup> <msup><mi>x</mi><mn>4</mn></msup> </mrow> <mrow><mi>d</mi><msup><mi>x</mi><mn>2</mn></msup></mrow> </mfrac>
厳格なマークアップへの対応付け
Mapping to Strict Markup
厳格なMathMLへの変換のために, 式の中では, 変数が, 実際のところ微分演算子によって束縛されていないことを, はっきり理解することが極めて重要です.
For the translation to strict Markup it is crucial to realize that in the expression case, the variable is actually not bound by the differentiation operator.
書き換え: diff
Rewrite: diff
が変数xの式である次の式があるとします.
Translate an expression
<apply><diff/> <bvar> </bvar> </apply>
この式は, 次の式に変換されます.
where
is an
expression in the variable x
to the expression
<apply>
<apply><csymbol cd="calculus1">diff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>微分された関数は, 厳格なマークアップで明確に自由変数の状態になった変数xに適用されます.
Note that the differentiated function is applied to the variable x making its status as a free variable explicit in strict markup. Thus the strict equivalent of
<apply><diff/> <bvar><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </apply>
よって, この式と等価な厳格なマークアップは, 次の式です.
is
<apply>
<apply><csymbol cd="calculus1">diff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>bvar要素がdegree要素を含んでいる場合, nthdiff記号が使われます.
If the bvar element contains a degree element, use the
nthdiff symbol.
書き換え: nthdiff
Rewrite: nthdiff
<apply><diff/> <bvar> <degree> </degree></bvar> </apply>
が変数xの式であるこの式は, 次の式に変換されます.
where
is an
is an expression in the variable x
is translated to to the expression:
<apply>
<apply><csymbol cd="calculus1">nthdiff</csymbol>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
</bind>
</apply>
</apply>例
For example
<apply><diff/> <bvar><degree><cn>2</cn></degree><ci>x</ci></bvar> <apply><sin/><ci>x</ci></apply> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply>
<apply><csymbol cd="calculus1">nthdiff</csymbol>
<cn>2</cn>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol><ci>x</ci></apply>
</bind>
</apply>
<ci>x</ci>
</apply>4.4.4.3 偏微分 <partialdiff/>
Partial Differentiation <partialdiff/>
| 種類 Class |
partialdiff |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
partialdiff partialdiffdegree |
partialdiff要素は, 複数の変数の関数または式に対する偏微分演算子要素です.
The partialdiff element is the partial differentiation operator element for
functions or expressions in several variables.
関数の偏微分の場合に, partialdiffを含む式は2つの引数を使用します. 1つ目は, 関数の引数が偏微分を構築する中で, 含まれている順番によって示される指数の一覧です. 2つ目は 偏微分される実際の関数です. 指数は繰り返されるかもしれません.
For the case of partial differentiation of a function, the
containing partialdiff takes two arguments: firstly a list of
indices indicating by position which function arguments are involved in
constructing the partial derivatives, and secondly the actual function
to be partially differentiated. The indices may be repeated.
コンテントMathML
Content MathML
<apply><partialdiff/> <list><cn>1</cn><cn>1</cn><cn>3</cn></list> <ci type="function">f</ci> </apply>
表示例
Sample Presentation
<mrow> <msub> <mi>D</mi> <mrow><mn>1</mn><mo>,</mo><mn>1</mn><mo>,</mo><mn>3</mn></mrow> </msub> <mi>f</mi> </mrow>
コンテントMathML
Content MathML
<apply><partialdiff/> <list><cn>1</cn><cn>1</cn><cn>3</cn></list> <lambda> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><ci>f</ci><ci>x</ci><ci>y</ci><ci>z</ci></apply> </lambda> </apply>
表示例
Sample Presentation
<mfrac> <mrow> <msup><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mn>3</mn></msup> <mrow> <mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><msup><mi>x</mi><mn>2</mn></msup></mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mi>z</mi></mrow> </mrow> </mfrac>
代数の式の場合, 囲っているapply要素の子要素である, bvar要素によって束縛変数が示されます. bvar要素は, その変数で行われる偏微分の階数を表すdegree要素を含むこともあるでしょう.
In the case of algebraic expressions, the bound variables are given by bvar
elements, which are children of the containing apply element. The bvar
elements may also contain degree element, which specify the order of the partial
derivative to be taken in that variable.
コンテントMathML
Content MathML
<apply><partialdiff/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply> </apply>
表示例
Sample Presentation
<mfrac> <mrow> <msup><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mn>2</mn></msup> <mrow> <mi>f</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>x</mi><mi>y</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mi>x</mi></mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mi>y</mi></mrow> </mrow> </mfrac>
微分の階数の合計は指定されなければならず, このことは, 1番上の階層での, すなわち, どの関連するbvarとでもなく, 囲っているapply要素の子要素としての, degree要素を利用して示されます.
Where a total degree of differentiation must be specified, this is
indicated by use of a degree element at the top level,
i.e. without any associated bvar, as a child of the
containing apply element.
コンテントMathML
Content MathML
<apply><partialdiff/>
<bvar><ci>x</ci><degree><ci>m</ci></degree></bvar>
<bvar><ci>y</ci><degree><ci>n</ci></degree></bvar>
<degree><ci>k</ci></degree>
<apply><ci type="function">f</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>表示例
Sample Presentation
<mfrac> <mrow> <msup><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><mi>k</mi></msup> <mrow> <mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi><mi>y</mi></mfenced> </mrow> </mrow> <mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><msup><mi>x</mi><mi>m</mi></msup></mrow> <mrow><mo>∂<!--PARTIAL DIFFERENTIAL--></mo><msup><mi>y</mi><mi>n</mi></msup></mrow> </mrow> </mfrac>
厳格なマークアップへの対応付け
Mapping to Strict Markup
関数に適用するとき, partialdiff要素は, calculus1コンテント辞書のpartialdiff記号に対応します. partialdiffの2つの引数を, 直接partialdiffの2つの引数に変換するのに, 何も特別な決まりは必要ありません.
When applied to a function, the partialdiff element
corresponds to the partialdiff
symbol from the calculus1 content dictionary. No special
rules are necessary as the two arguments of partialdiff
translate directly to the two arguments of
partialdiff.
書き換え: partialdiffdegree
Rewrite: partialdiffdegree
partialdiffが式とbvar修飾要素と一緒に利用される場合, partialdiffdegree記号を使って厳格なコンテントMathMLに書き換えられます.
If partialdiff is used with an expression and
bvar qualifiers it is rewritten to
Strict Content MathML using the
partialdiffdegree symbol.
<apply><partialdiff/> <bvar> <degree> </degree></bvar> <bvar> <degree> </degree></bvar> <degree> </degree> </apply>
は, 束縛変数を含む任意の式です.
is an
arbitrary expression involving the bound variables.
<apply>
<apply><csymbol cd="calculus1">partialdiffdegree</csymbol>
<apply><csymbol cd="list1">list</csymbol>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar> </bvar>
<bvar> </bvar>
</bind>
</apply>
</apply>束縛変数のどれかがdegree修飾要素を使用していないならば, <cn>1</cn>が階数の場所に用いられるべきです. 元の式がdegree修飾要素の合計を使用していなかったなら, partialdiffdegreeの2番目の引数は, 例えば次のように, 階数の合計となるべきです.
If any of the bound variables do not use a degree qualifier,
<cn>1</cn> should be used in place of the degree.
If the original expression did not use the total degree qualifier then
the second argument to partialdiffdegree
should be the sum of the degrees, for example
<apply><csymbol cd="arith1">plus</csymbol> </apply>
次の式があるとします.
With this rule, the expression
<apply><partialdiff/>
<bvar><ci>x</ci><degree><ci>n</ci></degree></bvar>
<bvar><ci>y</ci><degree><ci>m</ci></degree></bvar>
<apply><sin/>
<apply><times/><ci>x</ci><ci>y</ci></apply>
</apply>
</apply>上の決まりによって, この式は次の式に変換されます.
is translated into
<apply>
<apply><csymbol cd="calculus1">partialdiffdegree</csymbol>
<apply><csymbol cd="list1">list</csymbol>
<ci>n</ci><ci>m</ci>
</apply>
<apply><csymbol cd="arith1">plus</csymbol>
<ci>n</ci><ci>m</ci>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<apply><csymbol cd="transc1">sin</csymbol>
<apply><csymbol cd="arith1">times</csymbol>
<ci>x</ci><ci>y</ci>
</apply>
</apply>
</bind>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>4.4.4.4 発散 <divergence/>
Divergence <divergence/>
| 種類 Class |
unary-veccalc |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
divergence |
divergence要素は, しばしばdivと呼ばれるベクトル解析の発散演算子です. この要素は, スカラー値の関数のベクトルであるべき, ベクトル値の関数を意図した1つの引数を受け取り, その引数の発散を示すスカラー値を返す発散関数を表します.
The divergence element is the vector calculus divergence
operator, often called div. It represents the divergence function
which takes one argument which should be a vector of scalar-valued
functions, intended to represent a vector-valued function, and returns
the scalar-valued function giving the divergence of the argument.
コンテントMathML
Content MathML
<apply><divergence/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mi>div</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>a</mi></mfenced></mrow>
コンテントMathML
Content MathML
<apply><divergence/> <ci type="vector">E</ci> </apply>
表示例
Sample Presentation
<mrow><mi>div</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>E</mi></mfenced></mrow>
<mrow><mo>∇<!--NABLA--></mo><mo>⋅<!--DOT OPERATOR--></mo><mi>E</mi></mrow>
座標を定義する関数は, 座標の名前によって定義された式として, 明確に定義されるかもしれません. その場合には, 座標の名前は, 束縛変数として提供されなければなりません.
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
コンテントMathML
Content MathML
<apply><divergence/>
<bvar><ci>x</ci></bvar>
<bvar><ci>y</ci></bvar>
<bvar><ci>z</ci></bvar>
<vector>
<apply><plus/><ci>x</ci><ci>y</ci></apply>
<apply><plus/><ci>x</ci><ci>z</ci></apply>
<apply><plus/><ci>z</ci><ci>y</ci></apply>
</vector>
</apply>表示例
Sample Presentation
<mrow> <mi>div</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mo>(</mo> <mtable> <mtr><mtd> <mi>x</mi> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow> </mtd></mtr> <mtr><mtd> <mi>y</mi> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow><mi>x</mi><mo>+</mo><mi>z</mi></mrow> </mtd></mtr> <mtr><mtd> <mi>z</mi> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow><mi>z</mi><mo>+</mo><mi>y</mi></mrow> </mtd></mtr> </mtable> <mo>)</mo> </mrow>
4.4.4.5 勾配 <grad/>
Gradient <grad/>
| 種類 Class |
unary-veccalc |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
grad |
grad要素は, しばしばgradと呼ばれるベクトル解析の勾配演算子です. この要素は, スカラーの関数であるべき1つの引数を受け取り, 関数のベクトルを返す勾配関数を表すのに利用されます.
The grad element is the vector calculus gradient operator, often called
grad. It is used to represent the grad function, which takes one
argument which should be a scalar-valued function and returns a
vector of functions.
コンテントMathML
Content MathML
<apply><grad/><ci type="function">f</ci></apply>
表示例
Sample Presentation
<mrow><mi>grad</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>f</mi></mfenced></mrow>
<mrow><mo>∇<!--NABLA--></mo><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>f</mi></mfenced></mrow>
座標を定義する関数は, 座標の名前によって定義された式として, 明確に定義されるかもしれません. その場合には, 座標の名前は, 束縛変数として提供されなければなりません.
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
コンテントMathML
Content MathML
<apply><grad/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><times/><ci>x</ci><ci>y</ci><ci>z</ci></apply> </apply>
表示例
Sample Presentation
<mrow> <mi>grad</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mrow> <mo>(</mo> <mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow> <mi>x</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>y</mi><mo>⁢<!--INVISIBLE TIMES--></mo><mi>z</mi> </mrow> <mo>)</mo> </mrow> </mrow>
4.4.4.6 回転 <curl/>
Curl <curl/>
| 種類 Class |
unary-veccalc |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
curl |
curl要素は, ベクトル解析の回転関数を表すのに利用されます. この要素は, スカラー値の関数のベクトルであるべき, ベクトル値の関数の表現を意図した1つの引数を受け取り, 関数のベクトルを返します.
The curl element is used to represent the curl function
of vector calculus. It takes one argument which should be a vector
of scalar-valued functions, intended to represent a vector-valued
function, and returns a vector of functions.
コンテントMathML
Content MathML
<apply><curl/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mi>curl</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>a</mi></mfenced></mrow>
<mrow><mo>∇<!--NABLA--></mo><mo>×<!--MULTIPLICATION SIGN--></mo><mi>a</mi></mrow>
座標を定義する関数は, 座標の名前によって定義された式として, 明確に定義されるかもしれません. その場合には, 座標の名前は, 束縛変数として提供されなければなりません.
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
4.4.4.7 ラプラシアン <laplacian/>
Laplacian <laplacian/>
| 種類 Class |
unary-veccalc |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
Laplacian |
laplacian要素は, ベクトル解析のラプラシアン演算子を表します. ラプラシアンは, ベクトル値の関数を表す, スカラー値の関数のベクトルである単独の引数を受け取り, 関数のベクトルを返します.
The laplacian element represents the Laplacian operator of
vector calculus. The Laplacian takes a single argument which is a
vector of scalar-valued functions representing a vector-valued
function, and returns a vector of functions.
コンテントMathML
Content MathML
<apply><laplacian/><ci type="vector">E</ci></apply>
表示例
Sample Presentation
<mrow> <msup><mo>∇<!--NABLA--></mo><mn>2</mn></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>E</mi></mfenced> </mrow>
座標を定義する関数は, 座標の名前によって定義された式として, 明確に定義されるかもしれません. その場合には, 座標の名前は, 束縛変数として提供されなければなりません.
The functions defining the coordinates may be defined implicitly as expressions defined in terms of the coordinate names, in which case the coordinate names must be provided as bound variables.
コンテントMathML
Content MathML
<apply><laplacian/> <bvar><ci>x</ci></bvar> <bvar><ci>y</ci></bvar> <bvar><ci>z</ci></bvar> <apply><ci>f</ci><ci>x</ci><ci>y</ci></apply> </apply>
表示例
Sample Presentation
<mrow> <msup><mo>∇<!--NABLA--></mo><mn>2</mn></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mrow> <mo>(</mo> <mfenced><mi>x</mi><mi>y</mi><mi>z</mi></mfenced> <mo>↦<!--RIGHTWARDS ARROW FROM BAR--></mo> <mrow> <mi>f</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>x</mi><mi>y</mi></mfenced> </mrow> <mo>)</mo> </mrow> </mrow>
4.4.5 集合論
Theory of Sets
4.4.5.1 集合 <set>
Set <set>
| 種類 Class |
nary-setlist-constructor |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt, type? |
type属性の値type Attribute Values
|
"set" | "multiset" | 文字列 text |
| 内容 Content |
ContExp* |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
set, multiset |
setは, 引数から数学的集合を構築する関数を表します. この要素は, 複数項の関数です. 構築される集合の中身は, 構築要素の子要素として明確に示されるか, 第4.3.1.1節 構築要素の記号に対する入れ物マークアップで述べた決まりによって指定されるかするでしょう. 集合の要素には, 暗黙の順番は何もありません.
The set represents a function which constructs
mathematical sets from its arguments. It is an n-ary function. The
members of the set to be constructed may be given explicitly as
child elements of the constructor, or specified by rule as described
in Section 4.3.1.1 Container Markup for Constructor Symbols. There is no implied ordering to
the elements of a set.
コンテントMathML
Content MathML
<set> <ci>a</ci><ci>b</ci><ci>c</ci> </set>
表示例
Sample Presentation
<mrow>
<mo>{</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>}</mo>
</mrow>一般に, 集合は, 関数や適用範囲を準備しておくことでも構築されるでしょう. 集合の要素は, 範囲内の点で関数の値を求めることで得られる値と一致します.
In general, a set can be constructed by providing a function and a domain of application. The elements of the set correspond to the values obtained by evaluating the function at the points of the domain.
コンテントMathML
Content MathML
<set>
<bvar><ci>x</ci></bvar>
<condition>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
</condition>
<ci>x</ci>
</set>表示例
Sample Presentation
<mrow>
<mo>{</mo>
<mi>x</mi>
<mo>|</mo>
<mrow><mi>x</mi><mo><</mo><mn>5</mn></mrow>
<mo>}</mo>
</mrow>コンテントMathML
Content MathML
<set>
<bvar><ci type="set">S</ci></bvar>
<condition>
<apply><in/><ci>S</ci><ci type="list">T</ci></apply>
</condition>
<ci>S</ci>
</set>表示例
Sample Presentation
<mrow>
<mo>{</mo>
<mi>S</mi>
<mo>|</mo>
<mrow><mi>S</mi><mo>∈<!--ELEMENT OF--></mo><mi>T</mi></mrow>
<mo>}</mo>
</mrow>コンテントMathML
Content MathML
<set>
<bvar><ci> x </ci></bvar>
<condition>
<apply><and/>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
<apply><in/><ci>x</ci><naturalnumbers/></apply>
</apply>
</condition>
<ci>x</ci>
</set>表示例
Sample Presentation
<mrow>
<mo>{</mo>
<mi>x</mi>
<mo>|</mo>
<mrow>
<mrow><mo>(</mo><mi>x</mi><mo><</mo><mn>5</mn><mo>)</mo></mrow>
<mo>∧<!--LOGICAL AND--></mo>
<mrow>
<mi>x</mi><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">N</mi>
</mrow>
</mrow>
<mo>}</mo>
</mrow>4.4.5.2 リスト <list>
List <list>
| 種類 Class |
nary-setlist-constructor |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt, order |
order属性の値order Attribute Values
|
"numeric" | "lexicographic" |
| 内容 Content |
ContExp* |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
interval_cc, list |
list要素は, 引数からリストを構築する複数項の関数を表します. リストは, 要素に明確な順番があるという点で, 集合と異なります.
The list elements represents the n-ary function which
constructs a list from its arguments. Lists differ from sets in that
there is an explicit order to the elements.
リストの各要素や順番は, 明確に示されるでしょう.
The list entries and order may be given explicitly.
コンテントMathML
Content MathML
<list> <ci>a</ci><ci>b</ci><ci>c</ci> </list>
表示例
Sample Presentation
<mrow> <mo>(</mo><mi>a</mi><mo>,</mo><mi>b</mi><mo>,</mo><mi>c</mi><mo>)</mo> </mrow>
一般に, リストは, 関数や適用範囲を準備しておくことでも構築されるでしょう. リストの要素は, 範囲内の各点で関数の値を求めることで得られる値と一致します. この方法が利用される場合, リストの要素の順番は明確にはならないかもしれず, そのため, 順番の種類がorder属性によって指定されるかもしれません. lexicographic(訳注:辞書の順)とnumeric(訳注:数字の順)の2つの順番が用意されています.
In general a list can be constructed by providing a function and
a domain of application. The elements of the list correspond to the
values obtained by evaluating the function at the points of the
domain. When this method is used, the ordering of the list elements
may not be clear, so the kind of ordering may be specified by the
order attribute. Two orders are supported: lexicographic
and numeric.
コンテントMathML
Content MathML
<list order="numeric">
<bvar><ci>x</ci></bvar>
<condition>
<apply><lt/><ci>x</ci><cn>5</cn></apply>
</condition>
</list>表示例
Sample Presentation
<mrow> <mo>(</mo> <mi>x</mi> <mo>|</mo> <mrow><mi>x</mi><mo><</mo><mn>5</mn></mrow> <mo>)</mo> </mrow>
4.4.5.3 集合和 <union/>
Union <union/>
| 種類 Class |
nary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
union |
union要素は, 複数項の演算子である集合和を示すのに使われます. この要素は引数として集合を受け取り, それらの集合のいずれかに現れる要素を全て含む集合を示します.
The union element is used to denote the n-ary union of sets. It takes sets as arguments,
and denotes the set that contains all the elements that occur in any
of them.
引数は, 明確に示されるでしょう.
Arguments may be explicitly specified.
コンテントMathML
Content MathML
<apply><union/><ci>A</ci><ci>B</ci></apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>∪<!--UNION--></mo><mi>B</mi></mrow>
引数はまた, 第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で述べた修飾要素を使って指定されるかもしれません. 演算子要素は, 一連の集合の集合和を構築する束縛する演算子として使われるかもしれません.
Arguments may also be specified using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor). operator element can be used as a binding operator to construct the union over a collection of sets.
コンテントMathML
Content MathML
<apply><union/>
<bvar><ci type="set">S</ci></bvar>
<domainofapplication>
<ci type="list">L</ci>
</domainofapplication>
<ci type="set"> S</ci>
</apply>表示例
Sample Presentation
<mrow><munder><mo>⋃<!--N-ARY UNION--></mo><mi>L</mi></munder><mi>S</mi></mrow>
4.4.5.4 集合積 <intersect/>
Intersect <intersect/>
| 種類 Class |
nary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
intersect |
intersect要素は, 複数項の演算子である集合積を示すのに使われます. この要素は引数として集合を受け取り, それらの集合全てに現れる要素を全て含む集合を示します. それらの引数は, 囲っているapply要素によって明確に指定されるかもしれませんし, 第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で述べた修飾要素を使って指定されるかもしれません.
The intersect element is used to denote the n-ary
intersection of sets. It takes sets as arguments, and denotes the
set that contains all the elements that occur in all of them. Its arguments may be explicitly specified in the
enclosing apply element, or specified using qualifier
elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
コンテントMathML
Content MathML
<apply><intersect/> <ci type="set"> A </ci> <ci type="set"> B </ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>∩<!--INTERSECTION--></mo><mi>B</mi></mrow>
コンテントMathML
Content MathML
<apply><intersect/> <bvar><ci type="set">S</ci></bvar> <domainofapplication><ci type="list">L</ci></domainofapplication> <ci type="set"> S </ci> </apply>
表示例
Sample Presentation
<mrow><munder><mo>⋂<!--N-ARY INTERSECTION--></mo><mi>L</mi></munder><mi>S</mi></mrow>
4.4.5.5 集合の包摂 <in/>
Set inclusion <in/>
| 種類 Class |
binary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
in |
in要素は, 集合の包摂関係を表します. この要素は2つの引数, 要素と集合を持ちます. in要素は, その要素が与えられた集合に属することを示します.
The in element represents the set inclusion relation.
It has two arguments, an element and a set. It is used to denote
that the element is in the given set.
コンテントMathML
Content MathML
<apply><in/><ci>a</ci><ci type="set">A</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>∈<!--ELEMENT OF--></mo><mi>A</mi></mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のin記号が用いられるべきです.
When translating to Strict Content Markup, if the type
has value "multiset", then the in symbol from multiset1 should
be used instead.
4.4.5.6 集合の非包摂 <notin/>
Set exclusion <notin/>
| 種類 Class |
binary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
notin |
notinは, 否定された集合の包摂関係を表します. この要素は2つの引数, 要素と集合を持ちます. notinは, その要素が与えられた集合に属さないことを示します.
The notin represents the negated set inclusion
relation. It has two arguments, an element and a set. It is
used to denote that the element is not in the given set.
コンテントMathML
Content MathML
<apply><notin/><ci>a</ci><ci type="set">A</ci></apply>
表示例
Sample Presentation
<mrow><mi>a</mi><mo>∉<!--NOT AN ELEMENT OF--></mo><mi>A</mi></mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のin記号が用いられるべきです.
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.7 部分集合 <subset/>
Subset <subset/>
| 種類 Class |
nary-set-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
subset |
subset要素は, 部分集合関係を表します. この要素は, 1番目の引数が2番目の部分集合であることを示すのに使われます. 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, この要素は, 各引数がその後の引数の部分集合であることを表す, 複数項の演算子としても利用されるでしょう.
The subset element represents the subset relation. It is used to denote that the
first argument is a subset of the second. As described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln), it may also be used as an n-ary operator to express
that each argument is a subset of its predecessor.
コンテントMathML
Content MathML
<apply><subset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⊆<!--SUBSET OF OR EQUAL TO--></mo><mi>B</mi></mrow>
4.4.5.8 真部分集合 <prsubset/>
Proper Subset <prsubset/>
| 種類 Class |
nary-set-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
prsubset |
prsubset要素は, 真部分集合関係, すなわち, 1番目の引数が2番目の真部分集合であることを表します. 第4.3.4.3節 複数項の関係演算子(種類nary-reln, nary-set-reln)で述べたように, この要素は, 各引数がその後の引数の真部分集合であることを表す, 複数項の演算子としても利用されるでしょう.
The prsubset element represents the proper subset
relation, i.e. that the first argument is a proper subset of the
second. As described in Section 4.3.4.3 N-ary Relations (classes nary-reln, nary-set-reln), it may
also be used as an n-ary operator to express that each argument is a
proper subset of its predecessor.
コンテントMathML
Content MathML
<apply><prsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⊂<!--SUBSET OF--></mo><mi>B</mi></mrow>
4.4.5.9 部分集合でない <notsubset/>
Not Subset <notsubset/>
| 種類 Class |
binary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
notsubset |
notsubset要素は, 部分集合でない関係を表します. この要素は, 1番目の引数が2番目の部分集合でないことを示すのに使われます.
The notsubset element represents the negated subset
relation. It is used to denote that the first argument is not a subset of the
second.
コンテントMathML
Content MathML
<apply><notsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⊈<!--NEITHER A SUBSET OF NOR EQUAL TO--></mo><mi>B</mi></mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のin記号が用いられるべきです.
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.10 真部分集合でない <notprsubset/>
Not Proper Subset <notprsubset/>
| 種類 Class |
binary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
notprsubset |
notprsubset要素は, 真部分集合でない関係を表します. この要素は, 1番目の引数が2番目の真部分集合でないことを示すのに使われます.
The notprsubset element represents the negated proper
subset relation. It is used to denote that the first argument is not
a proper subset of the second.
コンテントMathML
Content MathML
<apply><notprsubset/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⊄<!--NOT A SUBSET OF--></mo><mi>B</mi></mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のin記号が用いられるべきです.
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.11 差集合 <setdiff/>
Set Difference <setdiff/>
| 種類 Class |
binary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
setdiff, setdiff |
setdiff要素は, 差集合演算子を表します. この要素は, 引数として2つの集合を受け取り, 1番目の集合に現れるが, 2番目の集合に現れない要素を全て含む集合を示します.
The setdiff element represents set difference
operator. It takes two sets as arguments, and denotes the set that
contains all the elements that occur in the first set, but not in
the second.
コンテントMathML
Content MathML
<apply><setdiff/> <ci type="set">A</ci> <ci type="set">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>∖<!--SET MINUS--></mo><mi>B</mi></mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のin記号が用いられるべきです.
When translating to Strict Content Markup, if the type has value "multiset", then
the in symbol from multiset1 should be used instead.
4.4.5.12 濃度 <card/>
Cardinality <card/>
| 種類 Class |
unary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
size, size |
card要素は, 集合の引数を受け取り, その濃度, すなわち, 集合の中の要素の数を返す濃度関数を表します. 集合の濃度は, 負でない整数または無限大の集合数です.
The card element represents the cardinality function,
which takes a set argument and returns its cardinality, i.e. the
number of elements in the set. The cardinality of a set is a
non-negative integer, or an infinite cardinal number.
コンテントMathML
Content MathML
<apply><eq/> <apply><card/><ci>A</ci></apply> <cn>5</cn> </apply>
表示例
Sample Presentation
<mrow> <mrow><mo>|</mo><mi>A</mi><mo>|</mo></mrow> <mo>=</mo> <mn>5</mn> </mrow>
厳格なコンテントMathMLに変換する場合, typeが値"multiset"を持つならば, 代わりにmultiset1のsize記号が用いられるべきです.
When translating to Strict Content Markup, if the type
has value "multiset", then the size symbol from multiset1 should be used
instead.
4.4.5.13 直積 <cartesianproduct/>
Cartesian product <cartesianproduct/>
| 種類 Class |
nary-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
cartesian_product |
cartesianproduct要素は, 直積演算子を表すのに使われます. この要素は, 引数として集合を受け取り, 囲っているapply要素によって明確に指定されるかもしれませんし, または第4.3.4.1節 複数項の演算子(種類nary-arith, nary-functional, nary-logical, nary-linalg, nary-set, nary-constructor)で述べた修飾要素を使って指定されるかもしれません.
The cartesianproduct element is used to represents the
Cartesian product operator. It takes sets as arguments, which may be
explicitly specified in the enclosing apply element, or
specified using qualifier elements as described in Section 4.3.4.1 N-ary Operators (classes nary-arith, nary-functional, nary-logical,
nary-linalg, nary-set, nary-constructor).
コンテントMathML
Content MathML
<apply><cartesianproduct/><ci>A</ci><ci>B</ci></apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>×<!--MULTIPLICATION SIGN--></mo><mi>B</mi></mrow>
4.4.6 数列と級数
Sequences and Series
4.4.6.1 総和 <sum/>
Sum <sum/>
| 種類 Class |
sum |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
sum |
sum要素は, 複数項の加算演算子を表します. 総和の各項は, 通常, 修飾要素の利用を通じて定められた決まりによって指定されます. この要素は, 引数の明確な一覧と一緒に利用できますが, その利用方法は避けられるべきで, そのような状況では代わりにplus演算子が使われるべきです.
The sum element represents the n-ary addition operator.
The terms of the sum are normally specified by rule through the use of
qualifiers. While it can be used with an explicit list of
arguments, this is strongly discouraged, and the plus
operator should be used instead in such situations.
sum演算子は, 明確な束縛変数と一緒に利用されるかもしれませんし, されないかもしれません. 束縛変数が用いられる場合, sum要素の後に, 添え字変数を示す1つ以上のbvar要素が続き, 添え字変数に対する定義域を示す修飾要素が続きます. applyで囲まれた最後の子要素は, 束縛変数による式で, 総和の各項は, 添え字変数の定義域の各点で, その式を計算することで得られます. 定義域の構造に従って, 総和の定義域は, 総和の上限と下限を指定するuplimitとlowlimitを用いてよく示されます.
The sum operator may be used either with or without
explicit bound variables. When a bound variable is used, the
sum element is followed by one or more bvar
elements giving the index variables, followed by qualifiers giving
the domain for the index variables. The final child in the enclosing
apply is then an expression in the bound variables, and the
terms of the sum are obtained by evaluating this expression at each
point of the domain of the index variables. Depending on the
structure of the domain, the domain of summation is often given
by using uplimit and lowlimit to specify upper and
lower limits for the sum.
何も束縛変数が示されていない場合, apply要素で囲まれた最後の子要素は関数でなければならず, 総和の各項は, 修飾要素で指定された定義域の各点で関数を計算することで得られます.
When no bound variables are explicitly given, the final child of
the enclosing apply element must be a function, and the
terms of the sum are obtained by evaluating the function at
each point of the domain specified by qualifiers.
コンテントMathML
Content MathML
<apply><sum/> <bvar><ci>x</ci></bvar> <lowlimit><ci>a</ci></lowlimit> <uplimit><ci>b</ci></uplimit> <apply><ci>f</ci><ci>x</ci></apply> </apply>
表示例
Sample Presentation
<mrow> <munderover> <mo>∑<!--N-ARY SUMMATION--></mo> <mrow><mi>x</mi><mo>=</mo><mi>a</mi></mrow> <mi>b</mi> </munderover> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
コンテントMathML
Content MathML
<apply><sum/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/><ci>x</ci><ci type="set">B</ci></apply>
</condition>
<apply><ci type="function">f</ci><ci>x</ci></apply>
</apply>表示例
Sample Presentation
<mrow> <munder> <mo>∑<!--N-ARY SUMMATION--></mo> <mrow><mi>x</mi><mo>∈<!--ELEMENT OF--></mo><mi>B</mi></mrow> </munder> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
コンテントMathML
Content MathML
<apply><sum/>
<domainofapplication>
<ci type="set">B</ci>
</domainofapplication>
<ci type="function">f</ci>
</apply>表示例
Sample Presentation
<mrow><munder><mo>∑<!--N-ARY SUMMATION--></mo><mi>B</mi></munder><mi>f</mi></mrow>
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
何も明確な束縛変数が用いられていない場合, 総和を厳格なコンテントMathMLに書き換えるのに, 修飾要素を用いた式を書き換える一般的な決まりを除いて, 何も特別な決まりは必要ありません. ただし, 束縛変数が用いられる場合, 束縛変数の式を関数として書き換えるのに, lambda構造を導入することが必要です.
When no explicit bound variables are used, no special rules are
required to rewrite sums as Strict Content beyond the generic rules
for rewriting expressions using qualifiers. However, when bound
variables are used, it is necessary to introduce a lambda
construction to rewrite the expression in the bound variables as a
function.
コンテントMathML
Content MathML
<apply><sum/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="arith1">sum</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>4.4.6.2 総積 <product/>
Product <product/>
| 種類 Class |
product |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
product |
product要素は, 複数項の乗算演算子を表します. 総積の各項は, 通常, 修飾要素の利用を通じて定められた決まりによって指定されます. この要素は, 引数の明確な一覧と一緒に利用できますが, その利用方法は避けられるべきで, そのような状況では代わりにtimes演算子が使われるべきです.
The product element represents the n-ary multiplication operator.
The terms of the product are normally specified by rule through the use of
qualifiers. While it can be used with an explicit list of
arguments, this is strongly discouraged, and the times
operator should be used instead in such situations.
product演算子は, 明確な束縛変数と一緒に利用されるかもしれませんし, されないかもしれません. 束縛変数が用いられる場合, product要素の後に, 添え字変数を示す1つ以上のbvar要素が続き, 添え字変数に対する定義域を示す修飾要素が続きます. applyで囲まれた最後の子要素は, 束縛変数による式で, 総積の各項は, 添え字変数の定義域の各点で, その式を計算することで得られます. 定義域の構造に従って, 定義域は, 一般にuplimitとlowlimitを用いて示されます.
The product operator may be used either with or without
explicit bound variables. When a bound variable is used, the
product element is followed by one or more bvar
elements giving the index variables, followed by qualifiers giving
the domain for the index variables. The final child in the enclosing
apply is then an expression in the bound variables, and the
terms of the product are obtained by evaluating this expression at
each point of the domain. Depending on the structure of the domain,
it is commonly given using uplimit and lowlimit
qualifiers.
何も束縛変数が示されていない場合, apply要素で囲まれた最後の子要素は関数でなければならず, 総積の各項は, 修飾要素で指定された定義域の各点で関数を計算することで得られます.
When no bound variables are explicitly given, the final child of
the enclosing apply element must be a function, and the
terms of the product are obtained by evaluating the function
at each point of the domain specified by qualifiers.
コンテントMathML
Content MathML
<apply><product/>
<bvar><ci>x</ci></bvar>
<lowlimit><ci>a</ci></lowlimit>
<uplimit><ci>b</ci></uplimit>
<apply><ci type="function">f</ci>
<ci>x</ci>
</apply>
</apply>表示例
Sample Presentation
<mrow> <munderover> <mo>∏<!--N-ARY PRODUCT--></mo> <mrow><mi>x</mi><mo>=</mo><mi>a</mi></mrow> <mi>b</mi> </munderover> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
コンテントMathML
Content MathML
<apply><product/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><in/>
<ci>x</ci>
<ci type="set">B</ci>
</apply>
</condition>
<apply><ci>f</ci><ci>x</ci></apply>
</apply>表示例
Sample Presentation
<mrow> <munder> <mo>∏<!--N-ARY PRODUCT--></mo> <mrow><mi>x</mi><mo>∈<!--ELEMENT OF--></mo><mi>B</mi></mrow> </munder> <mrow><mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi></mfenced></mrow> </mrow>
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
何も明確な束縛変数が用いられていない場合, 総積を厳格なコンテントMathMLに書き換えるのに, 修飾要素を用いた式を書き換える一般的な決まりを除いて, 何も特別な決まりは必要ありません. ただし, 束縛変数が用いられる場合, 束縛変数の式を関数として書き換えるのに, lambda構造を導入することが必要です.
When no explicit bound variables are used, no special rules are
required to rewrite products as Strict Content beyond the generic rules
for rewriting expressions using qualifiers. However, when bound
variables are used, it is necessary to introduce a lambda
construction to rewrite the expression in the bound variables as a
function.
コンテントMathML
Content MathML
<apply><product/> <bvar><ci>i</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <uplimit><cn>100</cn></uplimit> <apply><power/><ci>x</ci><ci>i</ci></apply> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="arith1">product</csymbol>
<apply><csymbol cd="interval1">integer_interval</csymbol>
<cn>0</cn>
<cn>100</cn>
</apply>
<bind><csymbol cd="fns1">lambda</csymbol>
<bvar><ci>i</ci></bvar>
<apply><csymbol cd="arith1">power</csymbol><ci>x</ci><ci>i</ci></apply>
</bind>
</apply>4.4.6.3 極限 <limit/>
Limits <limit/>
| 種類 Class |
limit |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
lowlimit, condition |
| OM記号 OM Symbols |
limit, both_sides, above, below, null |
limit要素は, 一連のものの極限を取る操作を表します. 極限点は, lowlimitとbvarを指定するか, conditionと1つ以上の束縛変数を指定することで表されます.
The limit element represents the operation of taking a limit of a
sequence. The limit point is expressed by specifying a lowlimit and a
bvar, or by specifying a condition on one or more bound variables.
コンテントMathML
Content MathML
<apply><limit/> <bvar><ci>x</ci></bvar> <lowlimit><cn>0</cn></lowlimit> <apply><sin/><ci>x</ci></apply> </apply>
表示例
Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→<!--RIGHTWARDS ARROW--></mo><mn>0</mn></mrow> </munder> <mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow> </mrow>
コンテントMathML
Content MathML
<apply><limit/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><tendsto/><ci>x</ci><cn>0</cn></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</apply>表示例
Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→<!--RIGHTWARDS ARROW--></mo><mn>0</mn></mrow> </munder> <mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow> </mrow>
コンテントMathML
Content MathML
<apply><limit/>
<bvar><ci>x</ci></bvar>
<condition>
<apply><tendsto type="above"/><ci>x</ci><ci>a</ci></apply>
</condition>
<apply><sin/><ci>x</ci></apply>
</apply>表示例
Sample Presentation
<mrow> <munder> <mi>lim</mi> <mrow><mi>x</mi><mo>→<!--RIGHTWARDS ARROW--></mo><msup><mi>a</mi><mo>+</mo></msup></mrow> </munder> <mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow> </mrow>
極限値に近付ける方向は, 厳格なコンテントMathMLでは, 方向指定要素both_sides, above, belowを提供する引数limitとして示されます. これらは, 後で説明するtendsto要素のtype属性の値"all", "above", "below"に対応します. null記号は, 何もtype属性がない場合に対応します.
The direction from which a limiting value is approached is given as an argument
limit in Strict Content MathML, which supplies the
direction specifier symbols both_sides, above, and below for this
purpose. The first correspond to the values "all", "above",
and "below" of the type attribute of the tendsto
element below. The null symbol corresponds to the case
where no type attribute is present. We translate
書き換え: 極限 condition
Rewrite: limits condition
<apply><limit/> <bvar> </bvar> <condition> <apply><tendsto/> 0</apply> </condition> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="limit1">limit</csymbol> 0 <csymbol cd="limit1"></csymbol> <bind><csymbol cd="fns1">lambda</csymbol> <bvar> </bvar> </bind> </apply>
が束縛変数と選択された記号を含む任意の式ならば, nullは, 上で述べたtendsto要素のtype属性に依存します.
where
is an
arbitrary expression involving the bound variable(s), and the choice of
symbol, null depends on the
type attribute of the tendsto element as
described above.
4.4.6.4 向かう <tendsto/>
Tends To <tendsto/>
| 種類 Class |
binary-reln |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt, type? |
type属性の値type Attribute Values
|
文字列 string |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
limit |
tendsto要素は, 数量が特定の値に向かう関係を表すのに用いられます. この要素は本来, 数学の極限の状態の一部ですが, それ自身の構造ゆえに, "xがyに向かう"といった数学の状態を捕えることを可能にすることや, より一般的な種類の極限を構築するための一部分を提供することがあります.
The tendsto element is used to express the relation that
a quantity is tending to a specified value. While this is used
primarily as part of the statement of a mathematical limit, it
exists as a construct on its own to allow one to capture
mathematical statements such as "As x tends to y," and to provide a
building block to construct more general kinds of limits.
tendsto要素は, 極限値に近づく方向を設定するために, 属性typeを利用します.
The tendsto element takes the attributes type to set the
direction from which the limiting value is approached.
コンテントMathML
Content MathML
<apply><tendsto type="above"/> <apply><power/><ci>x</ci><cn>2</cn></apply> <apply><power/><ci>a</ci><cn>2</cn></apply> </apply>
表示例
Sample Presentation
<mrow> <msup><mi>x</mi><mn>2</mn></msup> <mo>→<!--RIGHTWARDS ARROW--></mo> <msup><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo></msup> </mrow>
コンテントMathML
Content MathML
<apply><tendsto/>
<vector><ci>x</ci><ci>y</ci></vector>
<vector>
<apply><ci type="function">f</ci><ci>x</ci><ci>y</ci></apply>
<apply><ci type="function">g</ci><ci>x</ci><ci>y</ci></apply>
</vector>
</apply>表示例
Sample Presentation
<mfenced><mtable> <mtr><mtd><mi>x</mi></mtd></mtr> <mtr><mtd><mi>y</mi></mtd></mtr> </mtable></mfenced> <mo>→<!--RIGHTWARDS ARROW--></mo> <mfenced><mtable> <mtr><mtd> <mi>f</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi><mi>y</mi></mfenced> </mtd></mtr> <mtr><mtd> <mi>g</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>x</mi><mi>y</mi></mfenced> </mtd></mtr> </mtable></mfenced>
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
極限を修飾するtendstoの利用は, 決まり書き換え: 極限 conditionを通して厳格なコンテントMathMLの式を書くことで, 正式に定義されます. 他のより慣用的なtendstoの利用の意味は, 正式にはこの仕様書で定義されていません. これらの状況を厳格なコンテントMathMLに書き換える場合, tendstoは下に示すような付加情報の着いた識別子に書き換えられるべきです.
The usage of tendsto to qualify a limit is formally
defined by writing the expression in Strict Content MathML via the
rule Rewrite: limits condition. The meanings of other more
idiomatic uses of tendsto are not formally defined by this
specification. When rewriting these cases to Strict Content MathML,
tendsto should be rewritten to an annotated identifier as
shown below.
4.4.7 古典的な初等関数
Elementary classical functions
4.4.7.1 一般的な三角関数 <sin/>, <cos/>, <tan/>, <sec/>, <csc/>, <cot/>
Common trigonometric functions
<sin/>,
<cos/>,
<tan/>,
<sec/>,
<csc/>,
<cot/>
| 種類 Class |
unary-elementary |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
sin |
これらの演算子要素は, 標準的な三角関数を意味します. これらの標準的な解釈は広く知られており, これらをひとまとめに議論します.
These operator elements denote the standard trigonometric functions. Since their standard interpretations are widely known, they are discussed as a group.
コンテントMathML
Content MathML
<apply><sin/><ci>x</ci></apply>
表示例
Sample Presentation
<mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow>
コンテントMathML
Content MathML
<apply><sin/>
<apply><plus/>
<apply><cos/><ci>x</ci></apply>
<apply><power/><ci>x</ci><cn>3</cn></apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mi>sin</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mrow> <mo>(</mo> <mrow><mi>cos</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow> <mo>+</mo> <msup><mi>x</mi><mn>3</mn></msup> <mo>)</mo> </mrow> </mrow>
4.4.7.2 一般的な逆三角関数 <arcsin/>, <arccos/>, <arctan/>, <arcsec/>, <arccsc/>, <arccot/>
Common inverses of trigonometric functions
<arcsin/>,
<arccos/>,
<arctan/>,
<arcsec/>,
<arccsc/>,
<arccot/>
| 種類 Class |
unary-elementary |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
arcsin |
これらの演算子要素は, 標準的な三角関数の逆関数を意味します. 細かい定義は, これらの式が[Abramowitz1977]の定義に従うべきと評価する, 最も互換性のある適用方法に当てはまる利用方法によります.
These operator elements denote the inverses of standard trigonometric functions. Differing definitions are in use so for maximum interoperability applications evaluating such expressions should follow the definitions in [Abramowitz1977].
コンテントMathML
Content MathML
<apply><arcsin/><ci>x</ci></apply>
表示例
Sample Presentations
<mrow> <mi>arcsin</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mi>x</mi> </mrow>
<mrow> <msup><mi>sin</mi><mrow><mo>-</mo><mn>1</mn></mrow></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mi>x</mi> </mrow>
4.4.7.3 一般的な双曲線関数 <sinh/>, <cosh/>, <tanh/>, <sech/>, <csch/>, <coth/>
Common hyperbolic functions
<sinh/>,
<cosh/>,
<tanh/>,
<sech/>,
<csch/>,
<coth/>
| 種類 Class |
unary-elementary |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
sinh |
これらの演算子要素は, 標準的な双曲線関数を意味します. これらの標準的な解釈は広く知られており, これらは, ひとまとめに議論します.
These operator elements denote the standard hyperbolic functions. Since their standard interpretations are widely known, they are discussed as a group.
コンテントMathML
Content MathML
<apply><sinh/><ci>x</ci></apply>
表示例
Sample Presentation
<mrow><mi>sinh</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow>
4.4.7.4 一般的な逆双曲線関数 <arcsinh/>, <arccosh/>, <arctanh/>, <arcsech/>, <arccsch/>, <arccoth/>
Common inverses of hyperbolic functions
<arcsinh/>,
<arccosh/>,
<arctanh/>,
<arcsech/>,
<arccsch/>,
<arccoth/>
| 種類 Class |
unary-elementary |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
arcsinh |
これらの演算子要素は, 標準的な双曲線関数の逆関数を意味します. 細かい定義は, これらの式が[Abramowitz1977]の定義に従うと評価する, 最も互換性のある適用方法に当てはまる利用方法によります.
These operator elements denote the inverses of standard hyperbolic functions. Differing definitions are in use so for maximum interoperability applications evaluating such expressions should follow the definitions in [Abramowitz1977].
コンテントMathML
Content MathML
<apply><arcsinh/><ci>x</ci></apply>
表示例
Sample Presentations
<mrow> <mi>arcsinh</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mi>x</mi> </mrow>
<mrow> <msup><mi>sinh</mi><mrow><mo>-</mo><mn>1</mn></mrow></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mi>x</mi> </mrow>
4.4.7.5 指数 <exp/>
Exponential <exp/>
| 種類 Class |
unary-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
exp |
exp要素は, 自然対数関数の逆関数に結び付けられる指数関数を表します. この要素は, 1つの引数を受け取ります.
The exp element represents the exponentiation function
associated with the inverse of the ln function. It takes one
argument.
コンテントMathML
Content MathML
<apply><exp/><ci>x</ci></apply>
表示例
Sample Presentation
<msup><mi>e</mi><mi>x</mi></msup>
4.4.7.6 自然対数 <ln/>
Natural Logarithm <ln/>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
ln |
ln要素は, 自然対数関数を表します.
The ln element represents the natural logarithm function.
コンテントMathML
Content MathML
<apply><ln/><ci>a</ci></apply>
表示例
Sample Presentation
<mrow><mi>ln</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>a</mi></mrow>
4.4.7.7 対数 <log/>, <logbase>
Logarithm <log/>
, <logbase>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
logbase |
| OM記号 OM Symbols |
log |
log要素は, 与えられた底に関係する対数関数を表します. logbase修飾要素が存在するなら, 底を指定しています. そうでないならば, 底は10と見なされます.
The log elements represents the logarithm function
relative to a given base. When present, the logbase
qualifier specifies the base. Otherwise, the base is assumed to be 10.
apply.
コンテントMathML
Content MathML
<apply><log/> <logbase><cn>3</cn></logbase> <ci>x</ci> </apply>
表示例
Sample Presentation
<mrow><msub><mi>log</mi><mn>3</mn></msub><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow>
コンテントMathML
Content MathML
<apply><log/><ci>x</ci></apply>
表示例
Sample Presentation
<mrow><mi>log</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>x</mi></mrow>
厳格なコンテントMathMLへの対応付け
Mapping to Strict Content MathML
logを厳格なコンテントMathMLに対応付ける場合, 最初の引数によって指定される底に関係した, 2番目の引数の対数を返す関数を意味するlog記号を用いるでしょう. logbaseが存在するなら, 底を決定します. そうでないなら, 既定値の10が, 厳格なマークアップでは明確に提供されなければなりません. 次の例を参照して下さい.
When mapping log to Strict Content, one uses the
log symbol denoting the function
that returns the log of its second argument with respect to the base
specified by the first argument. When logbase is present, it
determines the base. Otherwise, the default base of 10 must be
explicitly provided in Strict markup. See the following example.
<apply><plus/>
<apply>
<log/>
<logbase><cn>2</cn></logbase>
<ci>x</ci>
</apply>
<apply>
<log/>
<ci>y</ci>
</apply>
</apply>
等価な厳格なコンテントMathML:
Strict Content MathML equivalent:
<apply>
<csymbol cd="arith1">plus</csymbol>
<apply>
<csymbol cd="transc1">log</csymbol>
<cn>2</cn>
<ci>x</ci>
</apply>
<apply>
<csymbol cd="transc1">log</csymbol>
<cn>10</cn>
<ci>y</ci>
</apply>
</apply>4.4.8 統計
Statistics
4.4.8.1 平均 <mean/>
Mean <mean/>
| 種類 Class |
nary-stats |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
mean, mean |
mean要素は, データの集合または確率変数の, 相加平均または平均を返す関数を表します.
The mean element represents the function returning arithmetic mean or average of a
data set or random variable.
コンテントMathML
Content MathML
<apply><mean/> <cn>3</cn><cn>4</cn><cn>3</cn><cn>7</cn><cn>4</cn> </apply>
表示例
Sample Presentation
<mrow> <mo>⟨<!--MATHEMATICAL LEFT ANGLE BRACKET--></mo> <mn>3</mn><mo>,</mo><mn>4</mn><mo>,</mo><mn>3</mn> <mo>,</mo><mn>7</mn><mo>,</mo><mn>4</mn> <mo>⟩<!--MATHEMATICAL RIGHT ANGLE BRACKET--></mo> </mrow>
コンテントMathML
Content MathML
<apply><mean/><ci>X</ci></apply>
表示例
Sample Presentation
<mrow><mo>⟨<!--MATHEMATICAL LEFT ANGLE BRACKET--></mo><mi>X</mi><mo>⟩<!--MATHEMATICAL RIGHT ANGLE BRACKET--></mo></mrow>
<mover><mi>X</mi><mo>¯<!--MACRON--></mo></mover>
厳格なマークアップへの対応付け
Mapping to Strict Markup
mean要素が引数の明確な一覧に適用される場合, 厳格なコンテントマークアップへの変換は, 書き換え: 要素で説明したように, s_data1コンテント辞書のmean記号を直接使用します. この要素が度数分布に適用される場合, s_dist1コンテント辞書のmean記号が使用されるべきです. 修飾要素と一緒の場合には, 書き換え: 複数項の演算子 domainofapplicationを注意事項も含め使用します.
When the mean element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the mean symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
mean symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use Rewrite: n-ary domainofapplication
with the same caveat.
4.4.8.2 標準偏差 <sdev/>
Standard Deviation <sdev/>
| 種類 Class |
nary-stats |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
sdev, sdev |
sdev要素は, データの集合または確立変数に対する標準偏差関数を示すのに使われます. 標準偏差は, 分散の平方根として与えられる, ばらつきの統計上の尺度です.
The sdev element is used to denote the standard deviation
function for a data set or random variable. Standard deviation is a
statistical measure of dispersion given by the square root of the
variance.
コンテントMathML
Content MathML
<apply><sdev/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
表示例
Sample Presentation
<mrow> <mo>σ<!--GREEK SMALL LETTER SIGMA--></mo> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
コンテントMathML
Content MathML
<apply><sdev/> <ci type="discrete_random_variable">X</ci> </apply>
表示例
Sample Presentation
<mrow><mo>σ<!--GREEK SMALL LETTER SIGMA--></mo><mo>⁡<!--FUNCTION APPLICATION--></mo><mfenced><mi>X</mi></mfenced></mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
sdev要素が引数の明確な一覧に適用される場合, 厳格なコンテントマークアップへの変換は, 書き換え: 要素で説明したように, s_data1コンテント辞書のsdev記号を直接使用します. この要素が度数分布に適用される場合, s_dist1コンテント辞書のsdev記号が使用されるべきです. 修飾要素と一緒の場合には, 書き換え: 複数項の演算子 domainofapplicationを注意事項も含め使用します.
When the sdev element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the sdev
symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
sdev symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use
Rewrite: n-ary domainofapplication with the same caveat.
4.4.8.3 分散 <variance/>
Variance <variance/>
| 種類 Class |
nary-stats |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ,DomainQ |
| OM記号 OM Symbols |
variance, variance |
variance要素は, データの集合または確率変数の分散を表します. 分散は, ばらつきの統計上の尺度で, 平均からの正の値の偏差を二乗して平均したものです.
The variance element represents the variance of a data set
or random variable. Variance is a statistical measure of dispersion,
averaging the squares of the deviations of possible values from their
mean.
コンテントMathML
Content MathML
<apply><variance/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
表示例
Sample Presentation
<mrow> <msup> <mo>σ<!--GREEK SMALL LETTER SIGMA--></mo> <mn>2</mn> </msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
コンテントMathML
Content MathML
<apply><variance/> <ci type="discrete_random_variable"> X</ci> </apply>
表示例
Sample Presentation
<mrow> <msup><mo>σ<!--GREEK SMALL LETTER SIGMA--></mo><mn>2</mn></msup> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mi>X</mi></mfenced> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
variance要素が引数の明確な一覧に適用される場合, 厳格なコンテントマークアップへの変換は, 書き換え: 要素で説明したように, s_data1コンテント辞書のvariance記号を直接使用します. この要素が度数分布に適用される場合, s_dist1コンテント辞書のvariance記号が使用されるべきです. 修飾要素と一緒の場合には, 書き換え: 複数項の演算子 domainofapplicationを注意事項も含め使用します.
When the variance element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the variance
symbol from the s_data1 content dictionary, as described in
Rewrite: element. When it is applied to a distribution, then the
variance symbol from the s_dist1 content
dictionary should be used. In the case with qualifiers use Rewrite: n-ary domainofapplication
with the same caveat.
4.4.8.4 中央値 <median/>
Median <median/>
| 種類 Class |
nary-stats |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| OM記号 OM Symbols |
median |
median要素は, 引数の中央値を返す演算子を表します. 中央値は, 標本の下半分を上半分と分ける数です.
The median element represents an operator returning the
median of its arguments. The median is a number separating the lower
half of the sample values from the upper half.
コンテントMathML
Content MathML
<apply><median/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
表示例
Sample Presentation
<mrow> <mi>median</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
median要素が引数の明確な一覧に適用される場合, 厳格なコンテントマークアップへの変換は, 書き換え: 要素で説明したように, s_data1コンテント辞書のmedian記号を直接使用します.
When the median element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the median
symbol from the s_data1 content dictionary, as described in
Rewrite: element.
4.4.8.5 最頻値 <mode/>
Mode <mode/>
| 種類 Class |
nary-stats |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| OM記号 OM Symbols |
mode |
mode要素は, 引数の最頻値を示すのに使われます. 最頻値は, 最もたくさん現れる値です.
The mode element is used to denote the mode of its arguments. The mode is
the value which occurs with the greatest frequency.
コンテントMathML
Content MathML
<apply><mode/> <cn>3</cn><cn>4</cn><cn>2</cn><cn>2</cn> </apply>
表示例
Sample Presentation
<mrow> <mi>mode</mi> <mo>⁡<!--FUNCTION APPLICATION--></mo> <mfenced><mn>3</mn><mn>4</mn><mn>2</mn><mn>2</mn></mfenced> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
mode要素が引数の明確な一覧に適用される場合, 厳格なコンテントマークアップへの変換は, 書き換え: 要素で説明したように, s_data1コンテント辞書のmode記号を直接使用します.
When the mode element is applied to an explicit list of arguments, the
translation to Strict Content markup is direct, using the mode
symbol from the s_data1 content dictionary, as described in
Rewrite: element.
4.4.8.6 積率 <moment/>, <momentabout>
Moment <moment/>, <momentabout>
| 種類 Class |
unary-functional |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| 修飾要素 Qualifiers |
degree, momentabout |
| OM記号 OM Symbols |
moment, moment |
moment要素は, データの集合または確率変数の, 集合のi次の積率を示すのに使われます. moment関数は, degreeとmomentabout修飾要素を受け取ります. degree構文が存在するなら, 積率の次数を意味します. 存在しなければ, 積率は, 1次の積率であると見なされます. momentと一緒に利用される場合, degree構文は, 1つの子要素を含むものとされています. momentabout構文が存在するなら, 積率が適用される際の原点を意味します. 存在しなければ, 積率は0に対する積率と見なされます.
The moment element is used to denote the ith moment of a set of data set or
random variable. The moment function accepts the degree and
momentabout qualifiers. If present, the degree schema denotes the order of
the moment. Otherwise, the moment is assumed to be the first order moment. When used with
moment, the degree schema is expected to contain a
single child. If present, the momentabout schema denotes the
point about which the moment is taken. Otherwise, the moment is
assumed to be the moment about zero.
コンテントMathML
Content MathML
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><mean/></momentabout> <cn>6</cn><cn>4</cn><cn>2</cn><cn>2</cn><cn>5</cn> </apply>
表示例
Sample Presentation
<msub> <mrow> <mo>⟨<!--MATHEMATICAL LEFT ANGLE BRACKET--></mo> <msup> <mfenced><mn>6</mn><mn>4</mn><mn>2</mn><mn>2</mn><mn>5</mn></mfenced> <mn>3</mn> </msup> <mo>⟩<!--MATHEMATICAL RIGHT ANGLE BRACKET--></mo> </mrow> <mi>mean</mi> </msub>
コンテントMathML
Content MathML
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><ci>p</ci></momentabout> <ci>X</ci> </apply>
表示例
Sample Presentation
<msub> <mrow> <mo>⟨<!--MATHEMATICAL LEFT ANGLE BRACKET--></mo><msup><mi>X</mi><mn>3</mn></msup><mo>⟩<!--MATHEMATICAL RIGHT ANGLE BRACKET--></mo> </mrow> <mi>p</mi> </msub>
厳格なマークアップへの対応付け
Mapping to Strict Markup
厳格なマークアップに書き換えるとき, s_data1コンテント辞書のmoment記号が, moment要素が引数の明確な一覧に適用される場合に用いられます. この要素が度数分布に適用される場合, s_dist1コンテント辞書のmoment記号が用いられるべきです. 両方の場合に, 演算子は, 最初の要素を次数として, 2番目の引数を原点として, その後のものをデータの集合または確率変数として, それぞれ受け取ります.
When rewriting to Strict Markup, the moment symbol from the s_data1 content
dictionary is used when the moment element is applied
to an explicit list of arguments. When it is applied to a distribution, then the
moment symbol from the s_dist1 content
dictionary should be used. Both operators take
the degree as the first argument, the point as the second, followed by
the data set or random variable respectively.
<apply><moment/> <degree><cn>3</cn></degree> <momentabout><ci>p</ci></momentabout> <ci>X</ci> </apply>
等価な厳格なコンテントMathML
Strict Content MathML equivalent
<apply><csymbol cd="s_dist1">moment</csymbol> <cn>3</cn> <ci>p</ci> <ci>X</ci> </apply>
4.4.9 線形代数
Linear Algebra
4.4.9.1 ベクトル <vector>
Vector <vector>
| 種類 Class |
nary-constructor |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| 内容 Content |
ContExp* |
| OM記号 OM Symbol |
vector |
ベクトルは, n次元のベクトル空間の要素を表す, 並べられたn個の値から成る要素です.
A vector is an ordered n-tuple of values representing an element of an n-dimensional vector space.
行列との相互作用や行列との掛け算の目的で, ベクトルは, 単独の列から成る行列と等価と見なされ, 転置したベクトルは, 単独の行から成る行列と等価と見なされます.
For purposes of interaction with matrices and matrix multiplication, vectors are regarded as equivalent to a matrix consisting of a single column, and the transpose of a vector as a matrix consisting of a single row.
vectorの各要素は, 子要素として明確に示されるか, 第4.3.1.1節 構築要素の記号に対する入れ物マークアップで述べた決まりによって指定されるかするでしょう.
The components of a vector may be given explicitly as
child elements, or specified by rule as described in Section 4.3.1.1 Container Markup for Constructor Symbols.
コンテントMathML
Content MathML
<vector> <apply><plus/><ci>x</ci><ci>y</ci></apply> <cn>3</cn> <cn>7</cn> </vector>
表示例
Sample Presentation
<mrow> <mo>(</mo> <mtable> <mtr><mtd><mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow></mtd></mtr> <mtr><mtd><mn>3</mn></mtd></mtr> <mtr><mtd><mn>7</mn></mtd></mtr> </mtable> <mo>)</mo> </mrow>
<mfenced> <mrow><mi>x</mi><mo>+</mo><mi>y</mi></mrow> <mn>3</mn> <mn>7</mn> </mfenced>
4.4.9.2 行列 <matrix>
Matrix <matrix>
| 種類 Class |
nary-constructor |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| 内容 Content |
ContExp* |
| OM記号 OM Symbol |
matrix |
行列は, 行列の行から形作られるものと見なされ, 各行はベクトルの特別な形と考えられます.
A matrix is regarded as made up of matrix rows, each of which can be thought of as a special type of vector.
matrixとmatrixrow要素のふるまいは, mtableやmtrプレゼンテーション要素と実質的に異なることに注意して下さい.
Note that the behavior of the matrix and matrixrow elements is
substantially different from the mtable and mtr presentation
elements.
matrix要素は, 構築要素で, そのため, 中身はそれぞれ, 子要素として明確に示されるか, 第4.3.1.1節 構築要素の記号に対する入れ物マークアップで述べて決まりによって指定されるかするでしょう. 後者の場合, 中身はそれぞれ, 関数と, その適用範囲である2次元の定義域を提供することで指定します. 行列の中身はそれぞれ, 定義域の各点で関数を計算することで得られた値に一致します.
The matrix element is a constructor
element, so the entries may be given explicitly as child elements,
or specified by rule as described in Section 4.3.1.1 Container Markup for Constructor Symbols. In the latter case, the
entries are specified by providing a function and a 2-dimensional
domain of application. The entries of the matrix correspond to
the values obtained by evaluating the function at the points of
the domain.
コンテントMathML
Content MathML
<matrix>
<bvar><ci type="integer">i</ci></bvar>
<bvar><ci type="integer">j</ci></bvar>
<condition>
<apply><and/>
<apply><in/>
<ci>i</ci>
<interval><ci>1</ci><ci>5</ci></interval>
</apply>
<apply><in/>
<ci>j</ci>
<interval><ci>5</ci><ci>9</ci></interval>
</apply>
</apply>
</condition>
<apply><power/><ci>i</ci><ci>j</ci></apply>
</matrix>表示例
Sample Presentation
<mrow> <mo>[</mo> <msub><mi>m</mi><mrow><mi>i</mi><mo>,</mo><mi>j</mi></mrow></msub> <mo>|</mo> <mrow> <msub><mi>m</mi><mrow><mi>i</mi><mo>,</mo><mi>j</mi></mrow></msub> <mo>=</mo> <msup><mi>i</mi><mi>j</mi></msup> </mrow> <mo>;</mo> <mrow> <mrow> <mi>i</mi> <mo>∈<!--ELEMENT OF--></mo> <mfenced open="[" close="]"><mi>1</mi><mi>5</mi></mfenced> </mrow> <mo>∧<!--LOGICAL AND--></mo> <mrow> <mi>j</mi> <mo>∈<!--ELEMENT OF--></mo> <mfenced open="[" close="]"><mi>5</mi><mi>9</mi></mfenced> </mrow> </mrow> <mo>]</mo> </mrow>
4.4.9.3 行列の行 <matrixrow>
Matrix row <matrixrow>
| 種類 Class |
nary-constructor |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 修飾要素 Qualifiers |
BvarQ, DomainQ |
| 内容 Content |
ContExp* |
| OM記号 OM Symbol |
matrixrow |
この要素は, 行列の行を表すのに利用される複数項の構築要素です.
This element is an n-ary constructor used to represent rows of matrices.
行列の行は, 行列の文脈の外では, それ自身で直接表示されることはありません.
Matrix rows are not directly rendered by themselves outside of the context of a matrix.
4.4.9.4 行列式 <determinant/>
Determinant <determinant/>
| 種類 Class |
unary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
determinant |
この要素は, 正方行列であるべき引数の行列式を返す, 単一項の関数に用いられます.
This element is used for the unary function which returns the determinant of its argument, which should be a square matrix.
コンテントMathML
Content MathML
<apply><determinant/> <ci type="matrix">A</ci> </apply>
表示例
Sample Presentation
<mrow><mi>det</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>A</mi></mrow>
4.4.9.5 転置行列 <transpose/>
Transpose <transpose/>
| 種類 Class |
unary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
transpose |
この要素は, 与えられた行列やベクトルの転置行列を意味する単一項の関数を表します.
This element represents a unary function that signifies the transpose of the given matrix or vector.
コンテントMathML
Content MathML
<apply><transpose/> <ci type="matrix">A</ci> </apply>
表示例
Sample Presentation
<msup><mi>A</mi><mi>T</mi></msup>
4.4.9.6 添え字 <selector/>
Selector <selector/>
| 種類 Class |
nary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
vector_selector, matrix_selector |
selector要素は, ベクトル, 行列, リストに添え字を付ける演算子です. この要素は, 1つ以上の引数を受け取ります. 最初の引数は, 選択が行われるベクトル, 行列, リストを特定し, 2番目や続く引数があるなら, 行われる選択の種類を指します.
The selector element is the operator for indexing into vectors, matrices
and lists. It accepts one or more arguments. The first argument identifies the vector,
matrix or list from which the selection is taking place, and the second and subsequent
arguments, if any, indicate the kind of selection taking place.
selector要素が単独の引数と一緒に用いられる場合, この要素は, 与えれたリスト, ベクトル, 行列の中の全ての一連の要素を示すものと解釈されます. 行列の一連の要素の順番は, 列の並び, 行の並びとなります. そのため, 出力されるリストは, 要素ごとの行列の行となります. つまり, 添え字が個々に行と列を示している行列(ai,j)に対して, 順番は, a1,1, a1,2, ... a2,1, a2,2 ... などとなるでしょう.
When selector is used with a single argument, it should be interpreted as
giving the sequence of all elements in the list, vector or matrix given. The ordering
of elements in the sequence for a matrix is understood to be first by column, then by
row; so the resulting list is of matrix rows given entry by entry.
That is, for a matrix (ai,j), where the indices denote row
and column, respectively, the ordering would be a1,1,
a1,2, ... a2,1, a2,2
... etc.
2つの引数が与えられており, 最初のものがベクトルまたはリストの場合, 2番目の引数は, リストまたはベクトルの要素の添え字を提供します. 最初の引数が行列の場合, 2番目の引数は, 行列の行の添え字を指定します.
When two arguments are given, and the first is a vector or list, the second argument specifies the index of an entry in the list or vector. If the first argument is a matrix then the second argument specifies the index of a matrix row.
3つの引数が与えられる場合, 最初のものがリストまたはベクトルであれば無視され, 行列の場合は, 2番目と3番目の引数が, 選ばれた要素の行の添え字と列の添え字を指定します.
When three arguments are given, the last one is ignored for a list or vector, and in the case of a matrix, the second and third arguments specify the row and column indices of the selected element.
コンテントMathML
Content MathML
<apply><selector/><ci type="vector">V</ci><cn>1</cn></apply>
表示例
Sample Presentation
<msub><mi>V</mi><mn>1</mn></msub>
コンテントMathML
Content MathML
<apply><eq/>
<apply><selector/>
<matrix>
<matrixrow><cn>1</cn><cn>2</cn></matrixrow>
<matrixrow><cn>3</cn><cn>4</cn></matrixrow>
</matrix>
<cn>1</cn>
</apply>
<matrix>
<matrixrow><cn>1</cn><cn>2</cn></matrixrow>
</matrix>
</apply>表示例
Sample Presentation
<mrow>
<msub>
<mrow>
<mo>(</mo>
<mtable>
<mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr>
<mtr><mtd><mn>3</mn></mtd><mtd><mn>4</mn></mtd></mtr>
</mtable>
<mo>)</mo>
</mrow>
<mn>1</mn>
</msub>
<mo>=</mo>
<mrow>
<mo>(</mo>
<mtable><mtr><mtd><mn>1</mn></mtd><mtd><mn>2</mn></mtd></mtr></mtable>
<mo>)</mo>
</mrow>
</mrow>4.4.9.7 外積 <vectorproduct/>
Vector product <vectorproduct/>
| 種類 Class |
binary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
vectorproduct |
この要素は, 外積を表します. この要素は, 2つの3次元ベクトルを受け取り, 3次元ベクトルの値を返します.
This element represents the vector product. It takes two three-dimensional vector arguments and represents as value a three-dimensional vector.
コンテントMathML
Content MathML
<apply><eq/>
<apply><vectorproduct/>
<ci type="vector"> A </ci>
<ci type="vector"> B </ci>
</apply>
<apply><times/>
<ci>a</ci>
<ci>b</ci>
<apply><sin/><ci>θ<!--GREEK SMALL LETTER THETA--></ci></apply>
<ci type="vector"> N </ci>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mrow><mi>A</mi><mo>×<!--MULTIPLICATION SIGN--></mo><mi>B</mi></mrow> <mo>=</mo> <mrow> <mi>a</mi> <mo>⁢<!--INVISIBLE TIMES--></mo> <mi>b</mi> <mo>⁢<!--INVISIBLE TIMES--></mo> <mrow><mi>sin</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>θ<!--GREEK SMALL LETTER THETA--></mi></mrow> <mo>⁢<!--INVISIBLE TIMES--></mo> <mi>N</mi> </mrow> </mrow>
4.4.9.8 内積 <scalarproduct/>
Scalar product <scalarproduct/>
| 種類 Class |
binary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
scalarproduct |
この要素は, 内積関数を表します. この要素は, 2つのベクトルの引数を受け取り, スカラーの値を返します.
This element represents the scalar product function. It takes two vector arguments and returns a scalar value.
コンテントMathML
Content MathML
<apply><eq/>
<apply><scalarproduct/>
<ci type="vector">A</ci>
<ci type="vector">B</ci>
</apply>
<apply><times/>
<ci>a</ci>
<ci>b</ci>
<apply><cos/><ci>θ<!--GREEK SMALL LETTER THETA--></ci></apply>
</apply>
</apply>表示例
Sample Presentation
<mrow> <mrow><mi>A</mi><mo>.</mo><mi>B</mi></mrow> <mo>=</mo> <mrow> <mi>a</mi> <mo>⁢<!--INVISIBLE TIMES--></mo> <mi>b</mi> <mo>⁢<!--INVISIBLE TIMES--></mo> <mrow><mi>cos</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>θ<!--GREEK SMALL LETTER THETA--></mi></mrow> </mrow> </mrow>
4.4.9.9 テンソル積 <outerproduct/>
Outer product <outerproduct/>
| 種類 Class |
binary-linalg |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
outerproduct |
この要素は, テンソル積関数を表します. この要素は2つのベクトルの引数を受け取り, 行列の値を返します.
This element represents the outer product function. It takes two vector arguments and returns as value a matrix.
コンテントMathML
Content MathML
<apply><outerproduct/> <ci type="vector">A</ci> <ci type="vector">B</ci> </apply>
表示例
Sample Presentation
<mrow><mi>A</mi><mo>⊗<!--CIRCLED TIMES--></mo><mi>B</mi></mrow>
4.4.10 定数要素と記号要素
Constant and Symbol Elements
この節は, 定数要素や記号要素の利用について説明します.
This section explains the use of the Constant and Symbol elements.
4.4.10.1 整数 <integers/>
integers <integers/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
Z |
この要素は, 正の整数, 負の整数, ゼロといった整数の集合を表します.
This element represents the set of integers, positive, negative and zero.
コンテントMathML
Content MathML
<apply><in/> <cn type="integer"> 42 </cn> <integers/> </apply>
表示例
Sample Presentation
<mrow><mn>42</mn><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">Z</mi></mrow>
4.4.10.2 実数 <reals/>
reals <reals/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
R |
この要素は, 実数の集合を表します.
This element represents the set of real numbers.
コンテントMathML
Content MathML
<apply><in/> <cn type="real"> 44.997</cn> <reals/> </apply>
表示例
Sample Presentation
<mrow> <mn>44.997</mn><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">R</mi> </mrow>
4.4.10.3 有理数 <rationals/>
Rational Numbers <rationals/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
Q |
この要素は, 有理数の集合を表します.
This element represents the set of rational numbers.
コンテントMathML
Content MathML
<apply><in/> <cn type="rational"> 22 <sep/>7</cn> <rationals/> </apply>
表示例
Sample Presentation
<mrow> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> <mo>∈<!--ELEMENT OF--></mo> <mi mathvariant="double-struck">Q</mi> </mrow>
4.4.10.4 自然数 <naturalnumbers/>
Natural Numbers <naturalnumbers/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
N |
この要素は, (ゼロを含む)自然数の集合を表します.
This element represents the set of natural numbers (including zero).
コンテントMathML
Content MathML
<apply><in/> <cn type="integer">1729</cn> <naturalnumbers/> </apply>
表示例
Sample Presentation
<mrow> <mn>1729</mn><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">N</mi> </mrow>
4.4.10.5 複素数 <complexes/>
complexes <complexes/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
C |
この要素は, 複素数の集合を表します.
This element represents the set of complex numbers.
コンテントMathML
Content MathML
<apply><in/> <cn type="complex-cartesian">17<sep/>29</cn> <complexes/> </apply>
表示例
Sample Presentation
<mrow> <mrow><mn>17</mn><mo>+</mo><mn>29</mn><mo>⁢<!--INVISIBLE TIMES--></mo><mi>i</mi></mrow> <mo>∈<!--ELEMENT OF--></mo> <mi mathvariant="double-struck">C</mi> </mrow>
4.4.10.6 素数 <primes/>
primes <primes/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
P |
この要素は, 正の素数の集合を表します.
This element represents the set of positive prime numbers.
コンテントMathML
Content MathML
<apply><in/> <cn type="integer">17</cn> <primes/> </apply>
表示例
Sample Presentation
<mrow><mn>17</mn><mo>∈<!--ELEMENT OF--></mo><mi mathvariant="double-struck">P</mi></mrow>
4.4.10.7 ネピア―の数 e <exponentiale/>
Exponential e <exponentiale/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
e |
この要素は, およそ2.718である自然対数の底を表します.
This element represents the base of the natural logarithm, approximately 2.718.
コンテントMathML
Content MathML
<apply><eq/> <apply><ln/><exponentiale/></apply> <cn>1</cn> </apply>
表示例
Sample Presentation
<mrow> <mrow><mi>ln</mi><mo>⁡<!--FUNCTION APPLICATION--></mo><mi>e</mi></mrow> <mo>=</mo> <mn>1</mn> </mrow>
4.4.10.8 虚数 i <imaginaryi/>
Imaginary i <imaginaryi/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
i |
この要素は, -1の平方根で一般にiと書かれる数学的定数を表します.
This element represents the mathematical constant which is the square root of -1, commonly written i
コンテントMathML
Content MathML
<apply><eq/> <apply><power/><imaginaryi/><cn>2</cn></apply> <cn>-1</cn> </apply>
表示例
Sample Presentation
<mrow><msup><mi>i</mi><mn>2</mn></msup><mo>=</mo><mn>-1</mn></mrow>
4.4.10.9 非数 <notanumber/>
Not A Number <notanumber/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
NaN |
この要素は, 非数の表記, すなわち不良設定の浮動小数点演算の結果を表します. [IEEE754]を参照して下さい.
This element represents the notion of not-a-number, i.e. the result of an ill-posed floating computation. See [IEEE754].
コンテントMathML
Content MathML
<apply><eq/> <apply><divide/><cn>0</cn><cn>0</cn></apply> <notanumber/> </apply>
表示例
Sample Presentation
<mrow> <mrow><mn>0</mn><mo>/</mo><mn>0</mn></mrow> <mo>=</mo> <mi>NaN</mi> </mrow>
4.4.10.10 真値 <true/>
True <true/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
true |
この要素は, ブール値の真値, すなわち, 真実に対する論理的定数を表します.
This element represents the Boolean value true, i.e. the logical constant for truth.
コンテントMathML
Content MathML
<apply><eq/>
<apply><or/>
<true/>
<ci type="boolean">P</ci>
</apply>
<true/>
</apply>表示例
Sample Presentation
<mrow> <mrow><mi>true</mi><mo>∨<!--LOGICAL OR--></mo><mi>P</mi></mrow> <mo>=</mo> <mi>true</mi> </mrow>
4.4.10.11 偽値 <false/>
False <false/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
false |
この要素は, ブール値の偽値, すなわち, 偽りに対する論理的定数を表します.
This element represents the Boolean value false, i.e. the logical constant for falsehood.
コンテントMathML
Content MathML
<apply><eq/>
<apply><and/>
<false/>
<ci type="boolean">P</ci>
</apply>
<false/>
</apply>表示例
Sample Presentation
<mrow> <mrow><mi>false</mi><mo>∧<!--LOGICAL AND--></mo><mi>P</mi></mrow> <mo>=</mo> <mi>false</mi> </mrow>
4.4.10.12 空集合 <emptyset/>
Empty Set <emptyset/>
| 種類 Class |
constant-set |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
emptyset, emptyset |
この要素は, 何も中身を含んでいない集合である空集合を表します.
This element is used to represent the empty set, that is the set which contains no members.
コンテントMathML
Content MathML
<apply><neq/> <integers/> <emptyset/> </apply>
表示例
Sample Presentation
<mrow> <mi mathvariant="double-struck">Z</mi><mo>≠<!--NOT EQUAL TO--></mo><mi>∅<!--EMPTY SET--></mi> </mrow>
厳格なマークアップへの対応付け
Mapping to Strict Markup
状況によっては, emptysetがemptysetに対応することは, 文脈から明らかかもしれません. しかしながら, このことを明確に示す方法は, 著者には付加情報を付け加えるほかにないことから, set1コンテント辞書のemptyset記号に変換することがいつでも無難です.
In some situations, it may be clear from context that emptyset
corresponds to the emptyset
However, as there is no method other than annotation for an author to explicitly indicate this,
it is always acceptable to translate to the emptyset symbol from the set1 CD.
4.4.10.13 円周率 <pi/>
pi <pi/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
pi |
この要素は, およそ3.142である, 円周と直径の比である円周率を表します.
This element represents pi, approximately 3.142, which is the ratio of the circumference of a circle to its diameter.
コンテントMathML
Content MathML
<apply><approx/> <pi/> <cn type="rational">22<sep/>7</cn> </apply>
表示例
Sample Presentation
<mrow> <mi>π<!--GREEK SMALL LETTER PI--></mi> <mo>≃<!--ASYMPTOTICALLY EQUAL TO--></mo> <mrow><mn>22</mn><mo>/</mo><mn>7</mn></mrow> </mrow>
4.4.10.14 オイラーの定数 <eulergamma/>
Euler gamma <eulergamma/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
gamma |
この要素は, およそ0.5772であるオイラーの定数を意味します.
This element denotes the gamma constant, approximately 0.5772.
コンテントMathML
Content MathML
<apply><approx/> <eulergamma/> <cn>0.5772156649</cn> </apply>
表示例
Sample Presentation
<mrow><mi>γ<!--GREEK SMALL LETTER GAMMA--></mi><mo>≃<!--ASYMPTOTICALLY EQUAL TO--></mo><mn>0.5772156649</mn></mrow>
4.4.10.15 無限大 <infinity/>
infinity <infinity/>
| 種類 Class |
constant-arith |
|---|---|
| 属性 Attributes |
CommonAtt, DefEncAtt |
| 内容 Content |
なし Empty |
| OM記号 OM Symbols |
infinity |
この要素は, 無限大の表記を表します.
This element represents the notion of infinity.
コンテントMathML
Content MathML
<infinity/>
表示例
Sample Presentation
<mi>∞<!--INFINITY--></mi>
4.5 非推奨のコンテント要素
Deprecated Content Elements
4.5.1 宣言 <declare>
Declare <declare>
| 属性 Attributes |
CommonAtt, type, scope, occurrence, definitionURL, encoding |
|---|---|
type属性type Attribute
|
宣言された識別子のMathML要素の型を定義します. defines the MathML element type of the identifier declared. |
scope属性scope Attribute
|
宣言の適用範囲を定義します. defines the scope of application of the declaration. |
nargs属性nargs Attribute
|
関数の宣言に対する引数の数. number of arguments for function declarations. |
occurrence属性の値occurrence Attribute values
|
"prefix" | "infix" | "function-model" |
definitionURL属性definitionURL Attribute
|
関数の詳細な意味を指し示すURI. URI pointing to detailed semantics of the function. |
encoding属性encoding Attribute
|
関数の詳細な意味の構文. syntax of the detailed semantics of the function. |
| 内容 Content |
ContExp, ContExp? |
MathML2は, 型のような特性を記号や変数に結び付け, 構造を共有するための短縮形を定義するのに, declare要素を提供していました. この要素は, MathML3では非推奨です. 構造の共有は, share要素を通して定義できます(詳しくは第4.2.7節 構造の共有 <share>を参照して下さい).
MathML2 provided the declare element to bind properties like
types to symbols and variables and to define abbreviations for structure sharing. This
element is deprecated in MathML 3. Structure sharing can obtained via the share
element (see Section 4.2.7 Structure Sharing <share> for details).
4.5.2 関係 <reln>
Relation <reln>
| 内容 Content |
ContExp* |
|---|
MathML1は, 等式または関係式を構築するのにreln要素を提供していました. この利用方法は, applyの方がより一般的に利用できることから, MathML2.0では非推奨とされました.
MathML1 provided the reln element to construct an equation or relation.
This usage was deprecated in MathML 2.0 in favor of the more generally usable apply.
4.5.3 関係 <fn>
Relation <fn>
| 内容 Content |
ContExp |
|---|
MathML1は, よく知られた数学関数の集合を拡張するのにfn要素を提供していました. この利用方法は, csymbolの方がより一般的に適用できることから, MathML2.0で非推奨とされました.
MathML1 provided the fn element to extend the collection of known mathematical
functions. This usage was deprecated in MathML 2.0 in favor of the more generally
applicable csymbol.
4.6 厳格なコンテントMathMLへの変換
The Strict Content MathML Transformation
MathML3は, 厳格なコンテントMathMLへの対応付けを定義することで, コンテントマークアップに意味を割り当てています. 厳格なMathMLは, 今度はOpenMathに1対1で対応し, この方法でコンテントMathMLの式から得られる式の部分は全て, 標準的なOpenMathコンテント辞書の集合を通して, 明確な意味を持ちます. 結果的に, 任意のコンテントMathMLの式の等価な厳格なコンテントMathMLへの対応付けは, コンテントMathMLの意味を補強する役割を担います.
MathML 3 assigns semantics to content markup by defining a mapping to Strict Content MathML. Strict MathML, in turn, is in one-to-one correspondence with OpenMath, and the subset of OpenMath expressions obtained from content MathML expressions in this fashion all have well-defined semantics via the standard OpenMath Content Dictionary set. Consequently, the mapping of arbitrary content MathML expressions to equivalent Strict Content MathML plays a key role in underpinning the meaning of content MathML.
任意のコンテントMathMLの厳格なコンテントMathMLへの対応付けは, アルゴリズムによって定義されます. このアルゴリズムは, 特定の厳格でない構造に適用される書き換えの決まりの集合として, 後で説明します. 個々の書き換えの変換方法は, 前の方の文章で詳細に説明してきました. この節の目的は, 1箇所に完全なアルゴリズムの概要を示すことです.
The mapping of arbitrary content MathML into Strict content MathML is defined algorithmically. The algorithm is described below as a collection of rewrite rules applying to specific non-Strict constructions. The individual rewrite transformations have been described in detail in context above. The goal of this section is to outline the complete algorithm in one place.
このアルゴリズムは, 一連の9つの段階で構成されています. 各段階は, 入力がそれ以上書き換えられなくなるまで繰り返し適用されます. XSLTといった多くのプログラミング言語において, 自然な実装は, 後の説明で述べられる並列の実装ではなく, 再帰的なアルゴリズムとしてのものです. XSLへの変換は, 簡単で, 最終的に同じ厳格なコンテントMathMLを提供します. ただし, 並列のアルゴリズムの全体構造は明らかなので, ここではその全体構造を式で示します.
The algorithm is a sequence of nine steps. Each step is applied repeatedly to rewrite the input until no further application is possible. Note that in many programming languages, such as XSLT, the natural implementation is as a recursive algorithm, rather than the multi-pass implementation suggested by the description below. The translation to XSL is straightforward and produces the same eventual Strict Content MathML. However, because the overall structure of the multi-pass algorithm is clearer, that is the formulation given here.
任意のコンテントMathMLの式を厳格なコンテントMathMLに変換するのに, 次のそれぞれの決まりを, 今度は対象である構造の全ての厳格でないコンテントMathMLが取り除かれるまで, 入力された式に適用します.
To transform an arbitrary content MathML expression into Strict Content MathML, apply each of the following rules in turn to the input expression until all instances of the target constructs have been eliminated:
-
厳格でない
bindの書き換えと非推奨の要素の除去: 束縛する式の外側のbindタグを, それらが修飾要素または複数の子要素を持っている場合,applyに変更します. このことは, 状況の区別無しに, 厳格でない束縛する式に適用される後々の決まりを認めることで, アルゴリズムを単純化しています. 後の決まりは, この段階で導入されたapply要素をbind要素に戻すように変更するであろうことに注意して下さい. また, この段階で, 非推奨のreln要素がapplyに書き換えられ,fn要素がそれら自身に囲まれている子要素の式に置き換えられます.Rewrite non-strict
bindand elminate deprecated elements: Change the outerbindtags in binding expressions toapplyif they have qualifiers or multiple children. This simplifies the algorithm by allowing the subsequent rules to be applied to non-strict binding expressions without case distinction. Note that the later rules will change theapplyelements introduced in this step back tobindelements. Also in this step, deprecatedrelnelements are rewritten toapply, andfnelements are replaced by the child expressions they enclose. -
修飾要素の慣用的な利用への特別な状況の決まりの適用:
Apply special case rules for idiomatic uses of qualifiers:
-
微分係数を, 書き換え: diff, 書き換え: nthdiff, 書き換え: partialdiffdegreeの決まりによって, 関係する変数の束縛された状態を展開するように書き換えます.
Rewrite derivatives with rules Rewrite: diff, Rewrite: nthdiff, and Rewrite: partialdiffdegree to explicate the binding status of the variables involved.
-
積分を, 書き換え: int, 書き換え: defint, 書き換え: defint 極限の決まりによって, 変数の束縛・自由の状態からあいまいさを取り除き,
lowlimit/uplimitの組みが与えられているなら積分範囲のあいまいさを取り除くように書き換えます.Rewrite integrals with the rules Rewrite: int, Rewrite: defint and Rewrite: defint limits to disambiguate the status of bound and free variables and of the orientation of the range of integration if it is given as a
lowlimit/uplimitpair. -
極限を, 書き換え: tendstoと書き換え: 極限 conditionで説明されていたように書き換えます.
Rewrite limits as described in Rewrite: tendsto and Rewrite: limits condition.
-
総和と総積を, 第4.4.6.1節 総和
<sum/>と第4.4.6.2節 総積<product/>で説明されていたように書き換えます.Rewrite sums and products as described in Section 4.4.6.1 Sum
<sum/>and Section 4.4.6.2 Product<product/>. -
根を, 第4.4.2.11節 根
<root/>で説明されていたように書き換えます.Rewrite roots as described in Section 4.4.2.11 Root
<root/>. -
対数を, 第4.4.7.7節 対数
<log/>,<logbase>で説明されていたように書き換えます.Rewrite logarithms as described in Section 4.4.7.7 Logarithm
<log/>,<logbase>. -
積率を, 第4.4.8.6節 積率
<moment/>,<momentabout>で説明されていたように書き換えます.Rewrite moments as described in Section 4.4.8.6 Moment
<moment/>,<momentabout>.
-
-
修飾要素の
domainofapplicationへの書き換え:これらの決まりは,bvarと修飾要素を使用している全てのapply構造を, 一般的なdomainofapplicationのみを使用した構造に書き換えます.Rewrite Qualifiers to
domainofapplication: These rules rewrite allapplyconstructions usingbvarand qualifiers to those using only the generaldomainofapplicationqualifier.-
範囲:
intervalやlowlimit/uplimitとして与えられる修飾要素を, 書き換え: interval 修飾要素を通して整数の範囲に書き換えます.Intervals: Rewrite qualifiers given as
intervalandlowlimit/uplimitto intervals of integers via Rewrite: interval qualifier. -
複数の
condition: 複数のcondition修飾要素を, それらを連結することで単独のものに書き換えます. その結果として結合されたconditionは, 書き換え: conditionの決まりによってdomainofapplicationに書き換えられます.Multiple
conditions: Rewrite multipleconditionqualifiers to a single one by taking their conjunction. The resulting compoundconditionis then rewritten todomainofapplicationaccording to rule Rewrite: condition. -
複数の
domainofapplication: 複数のdomainofapplication修飾要素を, 指定された定義域の共通部分を用いることで, 単独のものに書き換えます.Multiple
domainofapplications: Rewrite multipledomainofapplicationqualifiers to a single one by taking the intersection of the specified domains.
-
-
入れ物マークアップの標準化:
Normalize Container Markup:
-
集合やリストを, 書き換え: 複数項の集合やリスト domainofapplicationの決まりによって書き換えます.
Rewrite sets and lists by the rule Rewrite: n-ary setlist domainofapplication.
-
範囲, ベクトル, 行列, 行列の行を, 第4.4.1.1節 範囲
<interval>, 第4.4.9.1節 ベクトル<vector>, 第4.4.9.2節 行列<matrix>, 第4.4.9.3節 行列の行<matrixrow>で説明されていたように書き換えます. どの修飾要素もdomainofapplicationに書き換えられ, さらに段階6で書き換えられるであろうことに注意して下さい.Rewrite interval, vectors, matrices, and matrix rows as described in Section 4.4.1.1 Interval
<interval>, Section 4.4.9.1 Vector<vector>, Section 4.4.9.2 Matrix<matrix>and Section 4.4.9.3 Matrix row<matrixrow>. Note any qualifiers will have been rewritten todomainofapplicationand will be further rewritten in Step 6. -
ラムダ式を, 書き換え: lambdaと書き換え: lambda domainofapplicationの決まりによって書き換えます.
Rewrite lambda expressions by the rules Rewrite: lambda and Rewrite: lambda domainofapplication
-
区分的関数を, 第4.4.1.9節 区分的関数の定義
<piecewise>,<piece>,<otherwise>で説明されていたように書き換えます.Rewrite piecewise functions as described in Section 4.4.1.9 Piecewise declaration
<piecewise>,<piece>,<otherwise>.
-
-
domainofapplication修飾要素を使用した演算子に対する特別な状況の決まりの適用: この段階は, 第4.4節 具体的な演算子と定数に対するコンテントMathMLで導入された演算子に対する特別な状況を処理します. 異なる種類の考慮が必要な特別な状況があります.Apply Special Case Rules for Operators using
domainofapplicationQualifiers: This step deals with the special cases for the operators introduced in Section 4.4 Content MathML for Specific Operators and Constants. There are different classes of special cases to be taken into account:-
min,max,meanや同じような単一項または複数項の演算子を, 書き換え: 複数項または単一項の演算子 集合, 書き換え: 複数項または単一項の演算子 domainofapplication, 書き換え: 複数項または単一項の演算子 単独の引数の決まりによって書き換えます.Rewrite
min,max,meanand similar n-ary/unary operators by the rules Rewrite: n-ary unary set, Rewrite: n-ary unary domainofapplication and Rewrite: n-ary unary single. -
domainofapplicationを伴う修飾要素forallとexistsを, 書き換え: 量化記号の決まりによって, 含意と結合を用いた式に書き換えます.Rewrite the quantifiers
forallandexistsused withdomainofapplicationto expressions using implication and conjunction by the rule Rewrite: quantifier. -
domainofapplication要素と(状況に応じてbvarと)一緒に使用される積分を, 書き換え: intと書き換え: defintの決まりによって書き換えます.Rewrite integrals used with a
domainofapplicationelement (with or without abvar) according to the rules Rewrite: int and Rewrite: defint. -
domainofapplication要素と(状況に応じてbvarと)一緒に使用される総和と総積を, 第4.4.6.1節 総和<sum/>と第4.4.6.2節 総積<product/>で説明されていたように書き換えます.Rewrite sums and products used with a
domainofapplicationelement (with or without abvar) as described in Section 4.4.6.1 Sum<sum/>and Section 4.4.6.2 Product<product/>.
-
-
domainofapplicationの除去: この段階で, どのapplyも多くて1つのdomainofapplication子要素を持っており, 特別な場合は処理されてきています.domainofapplicationは, 厳格なコンテントMathMLではないことから, 次のように書き換えられます.Eliminate
domainofapplication: At this stage, anyapplyhas at most onedomainofapplicationchild and special cases have been addressed. Asdomainofapplicationis not Strict Content MathML, it is rewritten-
applyがbvar子要素を含んでいない場合, 書き換え: 制限の決まりを通して, 制限された関数の適用に書き換えられます.into an application of a restricted function via the rule Rewrite: restriction if the
applydoes not contain abvarchild. -
関係演算子と一緒に使用される場合, 書き換え: 複数項の関係演算子と書き換え: 複数項の関係演算子 bvarの決まりを通して, predicate_on_list記号の適用に書き換えられます.
into an application of the predicate_on_list symbol via the rules Rewrite: n-ary relations and Rewrite: n-ary relations bvar if used with a relation.
-
一般的な複数項の演算子の場合, 書き換え: 複数項の演算子 domainofapplicationの一般的な決まりを通して, apply_to_list記号を伴う構造に書き換えられます.
into a construction with the apply_to_list symbol via the general rule Rewrite: n-ary domainofapplication for general n-ary operators.
-
書き換え: apply bvar domainofapplicationの決まりを通して, 束縛変数を伴う
applyの中の, set1コンテント辞書のsuchthat記号を用いた構造に書き換えられます.into a construction using the suchthat symbol from the set1 content dictionary in an
applywith bound variables via the Rewrite: apply bvar domainofapplication rule.
-
-
厳格でない素子要素の書き換え:
Rewrite non-strict token elements:
-
type属性が"e-notation", "rational", "complex-cartesian", "complex-polar", "constant"のいずれか1つであるcn要素として表された数字を, 書き換え: cn sep, 書き換え: cn based_integer, 書き換え: cn constantの決まりを通して, 厳格なcnに書き換えます.Rewrite numbers represented as
cnelements where thetypeattribute is one of "e-notation", "rational", "complex-cartesian", "complex-polar", "constant" as strictcnvia rules Rewrite: cn sep, Rewrite: cn based_integer and Rewrite: cn constant. -
プレゼンテーションMathMLを含んでいる何らかの
ci,csymbol,cnを, 書き換え: cn プレゼンテーションMathMLと書き換え: ci プレゼンテーションMathMLの決まりと,csymbolに対して類似した決まりによって,semantics要素に書き換えます.Rewrite any
ci,csymbolorcncontaining presentation MathML tosemanticselements with rules Rewrite: cn presentation mathml and Rewrite: ci presentation mathml and the analogous rule forcsymbol.
-
-
演算子の書き換え: 第4.4節 具体的な演算子と定数に対するコンテントMathMLで定義された何らかの残りの演算子を, 書き換え: 要素の決まりによって, 構文の表で指定された記号を参照する
csymbolに書き換えます. 各演算子要素の説明で述べたように, 記号の適切な選択を決めるための, 特別な状況の決まりを必要とするものもあります. 特に注意すべき状況は次の場合です.Rewrite operators: Rewrite any remaining operator defined in Section 4.4 Content MathML for Specific Operators and Constants to a
csymbolreferencing the symbol identified in the syntax table by the rule Rewrite: element. As noted in the descriptions of each operator element, some require special case rules to determine the proper choice of symbol. Some cases of particular note are:-
selector演算子の引数の順番は, 書き換えられなければならず, 記号は, 引数の型によって決まります.The order of the arguments for the
selectoroperator must be rewritten, and the symbol depends on the type of the arguments. -
minus演算子に対する記号の選択は, 引数の数によって決まります.The choice of symbol for the
minusoperator depends on the number of the arguments. -
集合の演算子に対する記号の選択は, 引数の
typeの値によって決まることもあります.The choice of symbol for some set operators depends on the values of the
typeof the arguments. -
統計の演算子に対する記号の選択は, 引数の型の値によって決まることもあります.
The choice of symbol for some statistical operators depends on the values of the types of the arguments.
-
-
厳格でない属性の書き換え:
Rewrite non-strict attributes:
-
type属性の書き換え: この時点で,typeを持つ全ての要素は,ciとcsymbolを除いて, 型情報は演算子記号の選択に反映されており,type属性の無い等価な厳格なコンテントマークアップに書き換えられているべきです. 現時点で,type属性を持った残っているciとcsymbol要素を, 書き換え: ci type付加情報と書き換え: csymbol type付加情報の決まりによって,semanticsを持った厳格な式に書き換えます.Rewrite the
typeattribute: At this point, all elements that accept thetype, other thanciandcsymbol, should have been rewritten into Strict Content Markup equivalents withouttypeattributes, where type information is reflected in the choice of operator symbol. Now rewrite remainingciandcsymbolelements with atypeattribute to a strict expression withsemanticsaccording to rules Rewrite: ci type annotation and Rewrite: csymbol type annotation. -
definitionURLとencoding属性の書き換え:csymbol要素のdefinitionURLとencoding属性がコンテント辞書への参照として解釈できるならば(詳細は第4.2.3.2節<csymbol>の厳格でない利用を参照), 代わりにそれらをcd属性によるコンテント辞書への参照に書き換えます.Rewrite
definitionURLandencodingattributes: If thedefinitionURLandencodingattributes on acsymbolelement can be interpreted as a reference to a content dictionary (see Section 4.2.3.2 Non-Strict uses of<csymbol>for details), then rewrite to reference the content dictionary by thecdattribute instead. -
属性の書き換え: 厳格なマークアップで認められていない属性を持った何らかの要素を, それらの属性を除いた要素を最初の子要素にして, 書き換え: 属性の決まりによって
annotation要素の属性にしたsemantics構造に書き換えます.Rewrite attributes: Rewrite any element with attributes that are not allowed in strict markup to a
semanticsconstruction with the element without these attributes as the first child and the attributes inannotationelements by rule Rewrite: attributes.
-
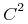
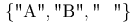
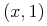
![{\left[{0},{1}\right]}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/interval1-interval_cc-ex1.gif)
![{\left({0},{1}\right]}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/interval1-interval_oc-ex1.gif)
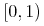
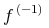
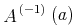
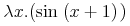
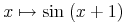
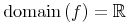
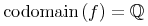
![{{\mathop{{\minormal{image}}}{\left({\minormal{sin}}\right)}}={\left[{\mn{-1}},{1}\right]}}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/fns1-image-ex1.gif)
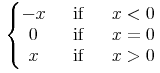
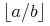
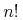
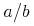
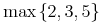
![{{\minormal{max}}{\left.\middle\{y^3\middle|{y\unicode{8712}{\left[{0},{1}\right]}}\middle\}\right.}}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/minmax1-big_max-ex1.gif)
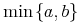

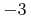
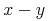
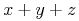
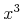
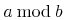
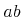
![\sqrt[{n}]{a}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/arith1-root-ex1.gif)
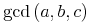
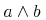
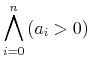
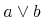
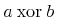
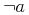
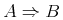
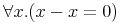
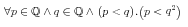
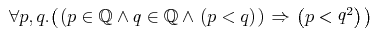
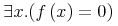
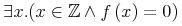
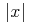
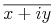
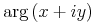
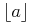
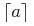
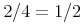
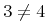
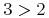
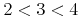
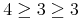
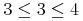
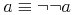
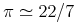
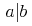
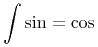
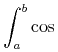
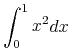
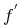
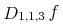
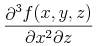
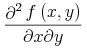
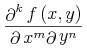
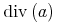
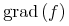
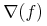
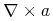
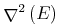
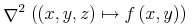
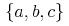
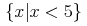
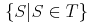
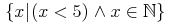
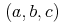
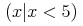
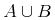
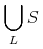
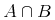
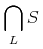
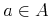
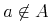
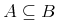
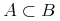
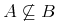
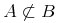
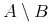
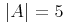
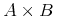
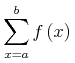
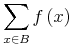
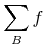
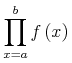
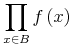
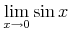
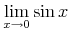
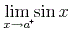
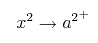
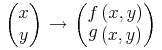
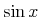
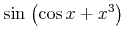
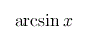
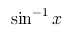
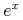
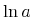
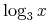
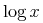
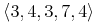
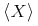
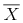
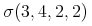
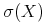


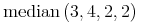
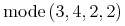
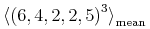
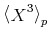
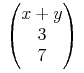
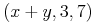
![{\left.[\msub{m}{{i,j}}\middle|{\msub{m}{{i,j}}=\msup{i}{j}};{{i\unicode{8712}{\left[1,5\right]}}\unicode{8743}{j\unicode{8712}{\left[5,9\right]}}}]\right.}](https://www.w3.org/TR/2014/REC-MathML3-20140410/image/linalg6-matrix-ex1.gif)